Нашей жизни теоремы

Нашей жизни теоремы

 Скоро мыслию по древу 
 Будут соки растекаться. 
 Скоро, скоро! Потерпите, 
 Не спешите разбегаться.

Вл. Соколов

Попробуем отказаться от ненадежной психологии в пользу строгой математики. Превратим жизненные проблемы в теоремы. Может быть, на этом пути удастся создать подлинный решатель любых задач?

Там, в геометрии, фигуры подчинены строгим законам; каков бы ни был треугольник, маленький или большой, равносторонний или разносторонний, подтянуто-прямоугольный или небрежно-тупоугольный, - в любом треугольнике сумма внутренних углов составляет 180 градусов. Видимо, и в житейской суете, в столкновении наших мыслей тоже возникают фигуры, тоже обозначаются углы, подвластные своим теоремам.

Я помню, какое сильное впечатление на меня, школьника, случайно прочитавшего томик философа Спинозы, произвела эта неожиданная и дерзкая идея. Мне казалось, что он отлил в строгие формы теорем не только наши мысли, но и душевные движения, но и эмоции, но и страсти - любовь и ненависть, дружбу и вражду, симпатии и антипатии. Противоречивые, хаотические, смутные, неуловимые, они приобрели под его пером изящную логическую форму: если... то... иначе...

"Если мы воображаем, что кто-либо причиняет удовольствие предмету, который мы ненавидим, то мы будем и его ненавидеть. Наоборот, если мы воображаем, что он причиняет этому предмету неудовольствие, мы будем любить его".

Ах, как славно теоремы Спинозы вписывались в школьные ситуации, как странно и неожиданно переплетались они со школьными уроками геометрии! Значительно позже, уже занимаясь вычислительными машинами, я осознал, что Спиноза в тех теоремах вовсе не создал исчисление эмоций. Для своих идей он выбрал внешнюю форму теорем, как выбирает поэт форму сонета или баллады.

И все же... Все же мысль обратить описания жизненных ситуаций в теоремы слишком соблазнительна, чтобы отказаться от нее. Лаксимы Спинозы логичны; и не в отсутствии логики их слабость. Их беда в другом. Изложенные на естественном, непринужденном, многоликом языке, они, увы, недоступны вычислительным машинам.

Совсем не таковы задачи, решаемые ЛЮБОЗАРом. Здесь условия заданы на однозначном языке математики, в виде формул исчисления предикатов. Искомая цель тоже предикатная запись. И, значит, есть "дано", есть "требуется доказать", есть настоящие теоремы.

Есть теоремы, нужен метод машинного их доказательства, алгоритм, способный доказать или опровергнуть любую теорему в узком исчислении предикатов. Такой алгоритм придуман недавно, и опробован, и работает безупречно. Он называется "метод резолюции".

Слово "резолюция" используется нами обычно в двух близких друг другу смыслах. Первый смысл хорошо выражен во фразе: "Собрание приняло резолюцию"; значит, не просто поговорили и разошлись, а выработали коллективное решение.

Второй смысл слова "резолюция" очевиден из предложения: "На моем заявлении начальник наложил резолюцию". Здесь "резолюция" - заключение ответственного лица, она и короче коллективной резолюции, и касается более узкого вопроса. В обоих случаях русское слово "резолюция" означает нечто законченное, готовое, продукт решения.

В латинском корне этого слова скрыт не только результат, но и действие, содержится процесс решения задачи, ход разрешения трудностей, последовательность получения заключений.

Резолюция в Искинте - это приспособленный к машине, подогнанный по ее мерке порядок логических решений, маршрут движения от исходных логических понятий к конечным выводам. Столбиками, отметками на маршруте являются резольвенты. Каждая из них извлекается из двух посылок; ее можно сравнить с общим знаменателем двух дробей или с касательной к двум окружностям, или со сплавом двух металлов, с бронзой времен Фидия и Аристотеля.

Аристотель имеет к резолюции и к резольвентам самое непосредственное отношение, ибо они дальние потомки аристотелевских умозаключений (силлогизмов). Помните знаменитое умозаключение; "Все люди смертны. Сократ - человек. Следовательно, Сократ смертен". Аристотель исследовал законы подобных умозаключений и предложил правила, по которым проверяется добротность силлогизма, выявляются скрытые ошибки, облегчается ведение споров.

Нашей жизни теоремы

У силлогизмов оказалась странная судьба. Нет, их не забыли навсегда после смерти Аристотеля. Наоборот, средневековые ученые всячески их лелеяли и развивали, обогащали тысячами примеров и контрпримеров, перекладывали в стихи, чтобы облегчить запоминание студентам. Средневековый студент давал только клятву, что выучил арифметику и геометрию, а по силлогизмам был жестокий экзамен; тут клятве не верили - требовали безупречных знаний.

В средневековой науке силлогизмы заняли королевское место. Их познание и применение, чаще всего в богословских спорах, вытесняло познание природы.

Вот почему ученые нового времени, враги средневековой схоластики, обрушили весь свой сарказм и ненависть на бедные аристотелевские силлогизмы. Для них силлогизмы и пустопорожняя болтовня были синонимами.

Р. Декарт так определил роль силлогизмов: они служат для того, "чтобы говорить без смысла о неизвестных вещах, вместо того чтобы познавать их".

Бесславно ушли силлогизмы с авансцены науки и занимали скромное место в учебниках логики, пока не явилась кибернетика, не извлекла их оттуда, не осветила новым и ярким светом.

Что речь идет о "неизвестных вещах" - беда исправимая. Если начинку для силлогизмов, их посылки готовят не профаны, а серьезные ученые, то в пирог войдут самые новые и достоверные факты опытной науки.

Что речь идет "без смысла", строго формально, так это в определенном смысле даже лучше: только строго формальная диета прописана вычислительной машине; понимать "по смыслу" она не умеет.

Главная беда аристотелевских силлогизмов в другом - в их неподвижности, в ждущем, сторожащем, вахтерском, что ли, характере. Они совсем не ищут новых идей, никак не участвуют в рождении новых мыслей, а служат лишь шаблонами для проверки готовых умозаключений: это по мерке, а это нет. Мертвые слепки вместо живых, переменчивых, развивающихся решений.

Придать силлогизмам движение, энергию, рыцарскую храбрость хотел дерзкий и несчастный Раймунд Луллий.

Почти до 30 лет Р. Луллий был придворным у арагонского короля Иакова, сочинял неплохие стихи, ухаживал за дамами. В 1263 году приключилась с ним памятная история.

Верхом он преследовал очаровательную молодую женщину, отпуская в ее адрес веселые и нескромные комплименты Женщина шла в церковь, а Р. Луллий настолько увлекся, что въехал в храм вслед за нею на коне. Дама с негодованием остановила рыцаря и сказала:

- Вы хотите видеть мою грудь, которой посвятили столько красочных эпитетов в своих сонетах? Ну что же, я могу доставить вам это удовольствие!

И женщина сбросила мантилью. Грудь ее оказалась пораженной кровоточащими язвами.

Р. Луллий испытал страшное потрясение. Он отказался от светских удовольствий и ушел в монахи, чтобы стать ученым, чтобы изобрести лекарство против всех человеческих недугов.

В тиши монастыря он понял, что изобретение универсального лекарства в высшей степени богоугодное дело, но еще важнее изобрести всеобщие приемы изобретения любых вещей, единые способы получения новых знаний.

Р. Луллий создал "Великое искусство", которое один из переводчиков его манускрипта на русский язык (перевод был сделан в XVII веке) назвал "ароматоуханным гроздеполезным овощем", - лучше, пожалуй, и не скажешь!

Принцип Р. Луллия состоял в следующем. В каждой отрасли знания имеется небольшое число основных идей. Составив все возможные комбинации этих идей, мы получим все знания, доступные ограниченному человеческому уму. Он. построил особую машину для комбинирования знаний. Машина представляла собой несколько вложенных друг в друга кругов с нанесенными на их борта символами понятий. Круги вращались друг относительно друга, понятия то совмещались, то расходились. Они были разноцветными, эти круги из пергамента, они создавали вокруг "великого искусства" Р. Луллия ореол таинственности и непостижимости.

Монах Р. Луллий был упорным проповедником истинной веры. Трижды отправлялся он в Африку, обращая в христианство местных магометан. Тем, видимо, это пришлось в конце концов не по вкусу. "Умер мучеником", - скупо сообщает церковная хроника о Р. Луллий.

Из многочисленных последователей Р. Луллия назовем Джордано Бруно, посвятившего теории и машине арагонского монаха целую книгу. Книгу эту читал, быть может, Свифт, во всяком случае, логическая машина, которую увидел Гулливер в лапутянской академии, - родная сестра разноцветных кругов Р. Луллия.

Академики в Лапуту заменили круги осями, на которые насадили кубики со словами. По команде учителя сорок его аспирантов вращали ручки осей, слова перемещались, возникали словосочетания, даже предложения, которые четверо самых талантливых учеников исправно записывали в особые книги.

Гулливеру объяснили, что это первый, самый важный этап исследований. На втором этапе предполагалась более легкая работа - сформировать из найденных слов исчерпывающие книги по всем областям знания.

Погодите смеяться, уважаемый читатель, алгоритм резолюции для вычислительных машин устроен подобным образом. Он потомок идей Аристотеля и Луллия; от Аристотеля взята строгость и полнота силлогизмов, от Луллия - живой, бойкий, деятельный, активный характер.

Резолюция не ждет, чтобы откуда-то принесли доводы-посылки для умозаключения, она сама их находит в условиях теоремы, сама собирает в пары. Резолюция не надеется, чтобы кто-то сделал очередной вывод, она сама извлекает резольвенту, единую и общую идею, скрытую в обеих посылках.

Силлогизм не берется и за холодную воду, а резолюция рада черной работе. Силлогизм спит в тенечке, а резолюция методично разрешает проблемы. Силлогизм просыпается на пустом месте, протирает лениво глаза, глядь, а резолюция вырастила целое дерево, дерево опровержений.

- Опять дерево? - удивляется силлогизм, а вместе с ним, быть может, и внимательный читатель.

- Да, опять дерево! - принужден согласиться автор. - Если бы меня попросили одним словом определить, что лежит в основе машинного разума, я ответил бы: дерево. Искинт, как Буратино, - деревянный человечек. Мы встречались уже на этих страницах с деревьями возможностей и целей, мы любовались синтаксическим деревом. Теперь выросло еще дерево опровержений...

- Вы называете свои теоретические построения деревьями для простоты? Небось в науке они иначе именуется?

- Ничего подобного. Их так и называют - деревья. Бывают конечные деревья и бесконечные деревья, развивается математика деревьев. Но прежде чем говорить о деревьях вообще, давайте познакомимся с деревом опровержений.

Нашей жизни теоремы

Оно растет не снизу вверх, не от земли к небу, как положено, а сверху вниз, от кроны к корню. Смыкается пара верхних ветвей - посылок, и в их слиянии родится плод - резольвента. Выбрасывает резольвента вниз новый побег, который сплетается с еще одной посылкой из условий теоремы. Вновь является резольвента, а дерево продолжается, опускается, растет, пока не исчерпаются все доводы-посылки. Тут достигает дерево своего корня, в котором и скрыт главный плод - опровержение.

Дерево опровержений - это наоборотное дерево, чьи ветви всегда собираются парами. Так велит метод резолюции.

Этот метод относится к самым крупным достижениям за все время работы в области Искинта. Найден алгоритм, свободный от человеческих слабостей, исчерпывающий все "за" и "против" и обязательно приводящий к результату. К реальному результату в реальной вычислительной машине!

Машина приобрела способность и вкус к умозаключениям, к логическим доказательствам, ей стали доступны "те длинные цепи", о которых напряженно думал Р. Декарт.

"Те длинные цепи простых и легких рассуждений, - писал он, - которыми обычно пользуются геометры, чтобы дойти до своих наиболее трудных доказательств, дали мне случай представить себе, что все вещи, которые могут стать предметом знания людей, связаны между собой таким же образом".

"Те длинные цепи" для разных, часто совсем не геометрических вещей кует сегодня вычислительная машина молотом резолюции.

Героиня задачи "Обезьяна и бананы" может отказаться от ненадежных услуг ЛЮБОЗАРа и предпочесть ему обязательную резолюцию. Впрочем, обезьяны давно пользовались методом резолюции, не ручаюсь за всех обезьян, но мартышки точно пользовались.

Об этом свидетельствует басня И. Крылова, в которой мартышка жаждет освоить очки: "то к тему их прижмет, то их на хвост нанижет, то их понюхает, то их полижет". Перебирает варианты, пытается извлечь хотя бы одну резольвенту, а не выходит, "очки не действуют никак". Мартышке, увы, надоедает перебор, она отказывается от резолюции, а могла бы после некоторого числа попыток приладить очки к глазам.

Программа для доказательства теорем в отличие от мартышки имеет железные нервы. Она спокойно перебирает все формально допустимые возможности. В задаче об обезьяне и бананах она даже пробует поставить ящик на голову обезьяне. Все логические атомы сопоставляются друг с другом, ни один камень не остается не перевернутым.

Резолюция вызывает энтузиазм специалистов, проявления которого очевидны, например, в отрывке из совсем свежей научной статьи: "Система доказательства теорем чарует и влечет. В самом деле, она универсальна, упорядочена и ее достоинства имеют подтверждение; опираясь на правильные входные данные, она весело и непринужденно приведет вас к искомому результату".

Итак, "мартышкин труд" предпочтительней эвристик. ЛЮБОЗАР с его колебаниями и отсутствием гарантий успешного решения должен уступить дорогу властной резолюции. Машинная логика сама, без человека одолеет любые препятствия.

Против этой достаточно распространенной постановки вопроса возражает академик В. Глушков: "Такая постановка не соответствует опыту, накопленному в других областях применения ЭВМ".

И предлагает совсем иной подход к машинному доказательству теорем. Центральной фигурой в нем является человек, квалифицированный математик, активно взаимодействующий с машиной. Чтобы взаимодействие было возможным, необходим язык, удобный для математика и понятный для ЭВМ. Чтобы взаимодействие было плодотворным, машину следует вооружить Алгоритмом Очевидности. Язык и Алгоритм - два краеугольных камня, на которых должно быть воздвигнуто новое здание "математического обеспечения для математических доказательств".

В. Глушков изложил свой новаторские идеи в начале 1965 года. Сейчас, в августе 1977 года, мы беседуем о развитии этих идей с ближайшим сотрудником В. Глушкова, профессором Ю. Капитоновой. Задаю ей естественный вопрос:

- Почему не доверить машине самой вести доказательство?

- При переборе всех возможностей, при выводе всех резольвент дерево опровержений становится великаном. Время решения задачи машиной достигает времени жизни нескольких поколений людей.

- Значит, я попрошу ЭВМ доказать теорему, а мой внук заберет готовое доказательство?

- На блюдечке с голубой каемочкой. Если, конечно, машина, ведущая перебор, не окажется в металлоломе, а само доказательство будет хоть кому-нибудь нужно.

- Все-таки память о дедушке... Как же хотите вы ускорить работу машины?

- Научив ее математике. Для этого и нужен особый язык, язык практической математики.

- Язык практической математики - зачем его придумывать вновь? Разве математика издавна не обладает своим строгим, точным и однозначным языком?

- Это распространенное заблуждение, что язык математики строг и однозначен. Точнее сказать, часть его именно такова - формулы. Но все остальное... Мы проанализировали десятки книг по современной математике и увидели, что словесная ткань, связки между формулами, - все эти "легко увидеть", "подобным же образом", "после некоторых преобразований", "из чего следует", - скорее намеки, чем объяснения. Они требуют от читателя додумывания, иногда несложной, а иногда большой мыслительной работы. В общении с машиной неопределенностям не место.

- Итак, язык практической математики делает аксиомы, теоремы, следствия - весь арсенал математики доступным машине. Но кто беседует с ЭВМ на этом языке, кто учит ее математике?

- Каждый, кому не лень. Я говорю серьезно: передача машине математических знаний - дело коллективное. Все математики должны хотеть, чтобы ЭВМ знала и фундаментальные вещи, и новейшие, только что опубликованные факты. Все математики будут стремиться к полноте и детальности машинных знаний.

- Отчего же такая забота о компьютере?

- Не о компьютере забота, а о себе. Знающая машина спасает математика от неловкости. Вообразите, вы прибегаете утром на работу и оповещаете своих коллег: "Сегодня ночью я решил десятую проблему Гильберта! Получился простенький алгоритм..." Вы ожидаете взрыва восторга, а в ответ несутся сдавленные смешки...

- Коллеги смеются, потому что десятую проблему решили раньше?

- Конечно! Но не только потому. Еще и потому, что запоздалое решение ошибочно - там нет никакого алгоритма, ни простого, ни сложного, там алгоритмическая неразрешимость... Вот если б незадачливый математик, прежде чем оповещать мир об открытии, сел бы за пульт ЭВМ и сообщил бы ей...

- Любопытно, как он говорил бы с машиной?

- Ну примерно так: "Пусть D - диофантово уравнение, пусть С - целые числа. Ввожу алгоритм проверки, имеет ли любое D решение в С. Сообщи новизну и корректность алгоритма".

- Как выглядел бы ответ машины?

- Категорически. "Новизна отсутствует. Десятая проблема Гильберта решена в 1969 году Ю. В. Матиясевичем. Нужна ли библиография?"

- То есть ЭВМ предлагает отпечатать список работ, в которых содержится решение?

- Само собой разумеется. Она перебрала свои математические знания, нашла относящиеся к делу и готова делиться ими с человеком.

- Прекрасно! Проверка новизны избавляет математиков не только от досады, но и от лишней работы. Ваш открыватель уже открытого мог обратиться к машине до бессонной ночи,, он мог узнать, стоит ли думать на \ десятой проблемой, или это зряшное занятие.

- Конечно. Но главное впереди. Машина не ограничивается проверкой новизны. Она проверяет правильность алгоритма, предложенного человеком. Она печатает дальше: "Ваш алгоритм некорректен. Ошибка состоит в следующем..."

- Для подобной проверки мало математических знаний. Нужны особые, тонкие умения.

- Справедливо. Здесь вступает в игру Алгоритм Очевидности - самое могучее наше оружие. Он шаг за шагом проверяет рассуждения человека. Никаких эмоций, никаких поблажек, голая логика. Если ход мысли человека постижим для него, если ему ясна правота или ошибочность, то он печатает результат, а если в рассуждениях математика содержатся бреши, просит заполнить их, вступает с математиком в диалог.

- Давайте представим себе, что я тот математик. Как общается со мной Алгоритм Очевидности?

- Он печатает: "Уважаемый Алексей Григорьевич, у вас из посылки А вытекает посылка В. На основании какой аксиомы или теоремы вы сделали данное заключение?"

- Я отвечаю: "Это интуитивно ясно".

- А он говорит: "Подумайте, на чем основана ваша интуиция. У меня нет подходящей аксиомы или теоремы. Может быть, вы пользуетесь аналогией? Сообщите, какую аналогию вы имеете в виду".

- Я отвечаю... Впрочем, уже ясно, что мы найдем общее решение: либо Алгоритм Очевидности вычислит мою правоту, либо я пойму собственную ошибку. Кстати, почему он так называется - Алгоритм Очевидности?

- О, здесь целая история! Вы знаете, самым любимым выражением математиков являются слова "очевидно, что". Пожалуй, у каждого на это магическое заклинание свой взгляд. Сколько ступенек преобразований можно пропустить без потери очевидности? Это зависит от квалификации математика, и от вкуса, и даже от порядочности. Один набивает свои работы тавтологиями, у него уже в самом начале очевидно, что находится в конце; другой в свободном полете мысли пропускает даже опорные пункты своего рассуждения. Легче самой доказать его теорему, чем ломать голову над авторскими "очевидно, что".

- Я вспомнил Блеза Паскаля. Мальчиком, читая "Начала" Эвклида, он возмущался: зачем приводятся

доказательства теорем, когда достаточно одних формулировок? Доказательства очевидны! Ваш Алгоритм Очевидности столь же проницателен?

- Нет, на сегодняшний день сила его "видения" примерно такая же, как у среднего выпускника вуза. Кое в чем он сильнее, например, в упрощении формул, а кое в чем слабее, скажем, в аналогиях. А в целом он вполне профессионален.

- Итак, ЭВМ является аккуратным собирателем математических знаний, педантичным проверяльщиком новизны и правильности, ловильщиком блох, может быть, даже составителем ехидных контрпримеров. Но способна ли машина к математическому творчеству? На первый случай, может ли она доказать новую теорему?

- Конечно! Человек сообщает ей свое предположение, интересное, но не доказанное им, а ЭВМ проводит полное доказательство.

- Успех гарантирован?

- Нет, но он очень вероятен. Либо Алгоритм Очевидности сам осилит доказательство, либо он позовет на помощь человека. Человек, надо надеяться, придумает вспомогательную теорему, а машина докажет ее, а человек тогда... В активном взаимодействии, в диалоге, перемещая границы очевидности друг друга, как картонные перегородки, партнеры отыщут доказательство.

- Которое ЭВМ тут же возьмет на заметку, включит в свой фонд доказательств, оприходует под номером 24 328, например...

- Для начала так она и поступит. Но как только у нее выдастся свободное от другой работы время, машина изучит новую теорему вдоль и поперек. Если эта теорема обобщает результаты нескольких других, то ЭВМ самостоятельно перестроит свои знания.

- Самостоятельно перестроит свои знания?

- Именно так. Наша машина не только знающий математик, она еще и современный математик. Она стремится всегда овладеть более общими, более сильными методами.

- Это касается и Алгоритма Очевидности?

- В первую очередь! В алгоритм наряду с методом резолюции должно влиться все яркое в области вывода, в том числе приемы узкие, но полезные.

- Вы говорите об эвристиках?

- Да, некоторые эвристики уже включены в Алгоритм Очевидности, дорога для других открыта. Без них в практической математике сегодня не обойтись.

- Остался один, пожалуй, главный вопрос: сможет ли машина самостоятельно находить новые теоремы, предлагать новые математические результаты?

- Это зависит от нашей способности выделять белые пятна, перспективные области в теории. Если область поиска очерчена, машина способна вскрыть все месторождения, получить все новые результаты. А уж глубоки ли они, красивы ли, полезны ли, судить человеку.

Работа Киевской школы теоретической кибернетики, о которой мы беседовали с Ю. Капитоновой, быстро продвигается вперед. Она, без сомнения, принесет громадную пользу самой математике. Не меньшего могут ждать от нее те, чьи интересы лежат в области практического Искинта. Программа - врач, или учитель, или юрист приобретает мощную, разнообразную, тщательно выверенную систему поиска следствий из заданных посылок.

А. Лавлейс, первая программистка, считала, что машина предназначена только для этой работы - для выведения следствий - и потому не способна сделать что-либо действительно новое. И сегодня немало людей разделяют ее пессимизм.

Следствия, однако, не всегда мельче, хуже, бледнее своих посылок. Скажем, лекарство от рака может оказаться дальним следствием известных фактов. Но разве поэтому оно не явится новостью, важнейшей, спасительной, желанной новостью для человечества? Лекарство, не исключено, скрывается на самой дальней ветке дерева возможностей. Тем труднее добраться до него, тем почетнее прийти к этому поистине величайшему следствию. Получение следствий - подлинно творческая работа.

Вот почему В. Глушков, касаясь логического мышления человека, говорит о том, что "хорошей (если не лучшей) модельной задачей здесь может служить задача автоматизации доказательства теорем в математике". Необходимо найти способы резкого сокращения блужданий и переборов, чтобы избежать абсурдных комбинаций, чтобы избавиться от нелепых альтернатив, чтобы действовать рационально, а не машинально.

Такие приемы недалеко лежат, они прекрасно известны специалистам по Искинту, это эвристики.

Сегодня метод резолюций дополнен эвристиками; эвристики вошли в самое нутро метода: машинная логика благодаря им стала результативной. Доказательства теорем, эта святая святых математики, не обошлись без эвристик. Выгнанная в дверь, психология вернулась через окно. Никуда от нее не деться!

Деревья опровержений, как и деревья возможностей, деревья целей и многие другие деревья Умного леса, нуждаются в эвристиках. Невольно возникает вопрос: эти деревья, что они? Условные значки, удобные и модные сегодня, или могучая метафора, связанная с нашими первоосновами, с глубинами человеческого мышления?

Судьбы мира связаны с деревьями, определяются деревьями - такова одна из самых древних идей человечества. В Европе, в Азии, в Африке, в Америке и. в Австралии - всюду, где первобытные люди в девственных лесах создавали человеческое общество, возникали мифы о мировом дереве.

В середине мира, говорит скандинавский миф, находится ясень Иггдрасиль, ветви его простираются над всем миром, вершина поднимается выше неба, а корни уходят в другие миры. Ясень Иггдрасиль - основа мира, его прошлое и будущее. На священном ясене был повешен бог Один, который претерпел мучения, чтобы изведать тайны мира.

Древние люди по-разному объясняли связь между подлинным, лесным, зеленым деревом и зыбкими, безместными, нетелесными человеческими мыслями. То они сажали человека или бога, решающего мучительную проблему, под священное дерево, то, чтобы связать их теснее, вешали на дерево, то сращивали их воедино, то придавали чудесную силу плодам священного дерева. В представлениях наших предков когда-то произошел удивительный переход от реального дерева, в ветвях которого гнездятся живые птицы, к воображаемому дереву, к дереву мысли.

Идея мирового дерева проникла в древнейшие письменные памятники человечества. Библия, например, подробно рассказывает о древе познания добра и зла.

Древо познания добра и зла... Перед внутренним взором каждого европейца возникает райский сад, и юные Адам и Ева, и дерево, отягченное запретными плодами, и змей-искуситель, обвивший ствол этого дерева.

А в памяти азиатов место этого дерева занимает дерево бодхи, дерево прозрения. Под ним, говорит легенда, сидел погруженный в созерцание Сиддхартха Гуатама. Здесь познал он смысл мира и жизни, нашел четыре благородные истины и стал пробужденным, просветленным, прозревшим, стал Буддой. Случилось это 2500 лет назад.

Буддисты всего мира до сих пор совершают паломничество в местечко Бодх-Гая на севере Индии. Там, рядом с храмом> растет огромный баньян - потомок легендарного дерева бодхи. Под ним плита, отмечающая место, где принимал свои решения Гуатама, а несколько сбоку каменное изваяние Будды в позе прозрения.

Дерево познания добра и зла и дерево бодхи внешне мало похожи друг на друга. Одно росло в воображаемой стране, другое в точно обозначенном месте. Одно - неведомо какой породы, а другое - баньян, разновидность фикусов. И тем не менее это родственные деревья.

Как хорошо сказал протопоп Аввакум, "по плоду во всяко древо познано бывает". У обоих деревьев одинаковые плоды: новые, неизведанные решения, иное будущее людей и мира.

Когда в мире появилась наука, мифические деревья отступили перед ее бульдозерами, выкорчевывающими суеверия. Мировое дерево поселилось в поэзии и живописи, а в науке остались лишь слабые его отзвуки. Ученые XVIII века растили только три сорта деревьев: родословные, иерархические и классификационные. Помните разговор между барином и мужиками в "Кому на Руси жить хорошо?". Пытаясь ошеломить мужиков, барин спрашивает:

 Скажите, вы, любезные, 
 О родословном дереве слыхали что-нибудь?

И слышит в ответ полные достоинства слова:

 Леса нам не заказаны - 
 Видали древо всякое, - 
 Сказали мужики. 

Они и вправду видали всякое дерево, кроме никчемного и кичливого родословного.

Социальные революции выкорчевывали и сжигали генеалогические деревья, эти символы неравенства, а ученые нашли им новое, неожиданное и воистину благородное применение. Ученые вооружились этими деревьями, излагая естественную историю живого мира, эволюцию видов. Позже родословные деревья пригодились для объяснения развития языков, наук и ремесел, машин и предметов быта.

Нашей жизни теоремы

Другой сорт распространенных в XVIII веке деревьев - иерархические. Иерархические деревья изображают связи господства и подчинения. Иерархия должностей в государстве, иерархия чинов в армии и в церкви, ветхозаветная "божественная иерархия": ангелы, херувимы, серафимы, архангелы и господь бог лично.

И третья порода деревьев XVIII века, пожалуй, самых любимых растений тогдашних ученых, - классификационные деревья. Как не любить и не холить эти метлы просвещения, наводящие строгий порядок в мире и в мыслях! Отличные образцы таких деревьев - классификация наук, сделанная еще в XVII веке Френсисом Беконом, и классификация животных - дерево, взлелеянное одним веком позже трудами Карла Линнея.

С развитием науки идея мирового дерева поблекла, почти стерлась и забылась. Если б не родословное, да иерархическое, да классификационное деревья, совсем бы пересох могучий поток метафор.

Современная наука очистила древний родник. Нам, как и доисторическим людям, идея дерева представляется волнующей, емкой и плодотворной. Почти погибшие умные деревья наполнились теперь новыми соками, выбросили новые побеги. Вновь зазеленел прекрасный лес, который растет нигде и всюду.

"Есть дерево: крик унимает, свет наставляет, больных исцеляет". Придумывая эту загадку, наши прадеды имели в виду березу. Сегодня у старой загадки иные отгадки. Дерево возможностей! Дерево целей! Дерево опровержений!

Впереди нас ждут встречи с новыми деревьями из Умного леса - с деревьями планов, с деревьями смыслов, с диагностическими деревьями. Но уже сейчас ясно, что представление малопохожих человеческих решений единым способом - в виде дерева, - могучее подспорье на пути к Искинту.

Вместо многочисленных частных, узких эвристик мы станем теперь изобретать единые способы выбора лишь полезных, лишь перспективных, лишь целенаправленных ветвей дерева.

Понедельник. Раннее утро. Перед выходом на работу вы подходите к окну. По небу несутся тяжелые тучи, а на градуснике 25 тепла. "Одевать ли плащ? - размышляете вы. - Если будет дождь, плащ окажется кстати, а если пронесет, придется зря таскаться с ним по жаре. Полезно, конечно, послушать прогноз погоды. Минут через пять по радио скажут, ожидается ли дождь. Но время дорого - пропустишь автобус, да и прогнозу можно верить лишь с оглядкой".

Итак, снова дерево. Его корень "выбор одежды" расщепляется на два ствола: "ждать прогноза" и "не ждать прогноза". Положим, вы решили ждать. И спустя пять минут слышите прогноз: ожидается дождь.

"Опять, - думаете вы, - опять синоптики обещают дождь. Вчера тоже обещали. И позавчера. А дождя не было; все их прогнозы - обман".

И вы оставляете плащ на вешалке. И, отчаянно спеша, выбегаете на улицу. А дождь не заставляет себя ждать. Насквозь промокший и слегка опоздавший, вы являетесь на работу, извлекаете из кармана листок с деревом "выбор одежды" и внимательно рассматриваете другие возможности.

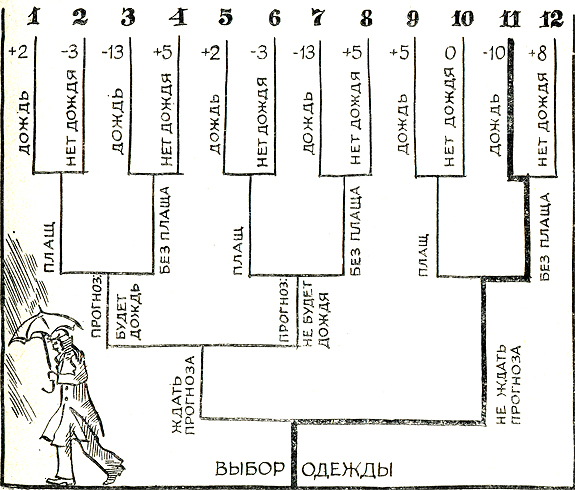
Всего в кроне дерева двенадцать ветвей. Теперь-то ясно, что незачем было бежать без плаща под дождь; ветви 3, 7 и 11 следовало решительно отбросить. Нужно было согласиться с прогнозом, взять плащ и оказаться в выигрыше, то есть выбрать ветвь 1. Даже если бы радио сказало "не будет дождя", даже тогда стоило бы взять плащ - перестраховаться (ветвь 5). Да и вообще, при чем здесь прогноз? Увидел, что облачно, надевай плащ, не надейся на авось (ветвь 9).

Столь мрачно вы рассуждаете оттого, что дождь, проливной и холодный, не оставил на вас сухого места. Задержись он на часок, вы благополучно добрались бы до работы. Тогда б выигрышными оказались ветви 4, 8 и 12 (вы без плаща, и нет дождя).

На дереве есть еще ветви 2, 6 и 10 (вы в плаще, на улице солнышко); лучше ли это, чем быть без плаща в дождь, - решать вам самому.

Нашей жизни теоремы

В том-то и состоит трудность, что решать надо, не зная наверняка, будет ли дождь. Для такого неопределенного решения можно оценить пользу от своих действий в баллах.

Если вы не ждали прогноза, не взяли плащ и дождя не было, то удовольствие от правильного решения резонно оценить в +8 баллов (ветвь 12). Самый печальный случай когда вы понадеялись на прогноз, не взяли плащ, а хлынул дождь; этой вдвойне досадной ситуации припишем -13 баллов (ветвь 3).

Каждая из ветвей дерева получает свою оценку. На рисунке показаны оценки, удовлетворяющие автора; читатель вправе назначить другие баллы. Столь же субъективна наша оценка вероятности того, что произойдет дождь или. что бюро прогнозов ошибается.

Оценки назначаются по вашей воле, но на этом своеволие кончается, и начинается математика. Формулы статистической теории принятия решений позволяют найти на дереве ветвь, наилучшую в данных условиях, при данных оценках. Если до прогноза вы считали дождь вероятным на 40 процентов, если сам прогноз погоды сбывается в 70 процентах случаев, то расчет по алгоритму статистических решений приводит к категорическому выводу: прогноза ждать не стоит. И брать с собой плащ тоже не стоит.

Вы зря ждали радиосообщения, но, выйдя без плаща поступили правильно. Пусть шальной дождь застиг вас по дороге - все равно правильно! Это подсчитано с помощью статистической теории принятия решений, области математики, на которую часто опирается Искинт.

Статистическая теория принятия решений не помогла вам сегодня. Зато во многие другие облачные понедельники вы благополучно избежите дождя. Эта теория умело отсекает многочисленные ветви дерева, выбирая в густой кроне самый выгодный путь. Наряду со статистической теорией принятия решений в программах Искинта трудятся и другие эвристики - веткорубы. "Сначала вширь" зовут одну из них: "сначала вглубь" - имя другой; "не зарываться" - девиз третьей. Все они. хотя и по-разному, стремятся к одной цели: заменить слепой перебор ветвей дерева разумной оценкой правильного пути.

Эвристики, вошедшие в метод доказательства теорем, в метод резолюции, усиливают, но одновременно и ослабляют его: вот-вот потеряется обязательность достижения результата. Приходится балансировать на зыбкой грани между изяществом и результативностью.

Что ж, разработка Искинта - это инженерное дело, а не чистая математика или чистая психология. Здесь все замешено на компромиссах. Выбор инженера определяется практической полезностью, а не теоретической безупречностью. Что выбрать в качестве решателя задач для робота - анализ средств и целей или резолюцию? У каждого подхода есть сильные стороны, есть и недостатки.

"Возьму оба! - решает инженер. - Пусть, составляя свои планы в общем, робот действует по программе ЛЮБОЗАР, а уточняя частности, переходя от стратегии к тактике, доказывает теоремы".

Инженера не смущают действия робота по разнородным программам, лишь бы работал, лишь бы давал наибольший эффект. Инженер понимает, что компромиссы только начинаются. Его робот действует не в абстрактном мире логики, а в реальном, грубом мире с помехами, трением, осечками и глупостью. Отправилась, скажем, "разумная тележка" за наклонной плоскостью, а у нее заело колесо; робот вращается на месте, не двигаясь вперед. Или в другой раз удалось подтолкнуть наклонную плоскость к платформе, въехать по ней на платформу, но вдруг передние колеса тележки-робота провалились в зазор между плоскостью и платформой. Или потеря питания, или случайный предмет на дороге, или...

Их невозможно перечислить, все эти "или", невозможно заранее предусмотреть все каверзы, которые готовит реальный мир наивному роботу. Если он займется составлением планов на все случаи жизни, то переберет миллионы целей и средств, докажет тысячи теорем, но никогда не сдвинется с места. Если же робот пренебрежет превратностями жизни и понадеется на авось, то скорее всего попадет впросак.

Нужен компромисс между тщательностью планирования и быстротой исполнения, нужна способность менять свои планы по ходу дела, способность, которой обладает человек.

Я расскажу вам сейчас старинную историю о корректировке планов.

Дело происходило в давние времена в Лондоне. Честный купец взял большую сумму денег взаймы у ростовщика и не смог отдать в срок. Ему грозит позор и долговая тюрьма, его красавице дочери - голодное, жалкое существование.

Есть, впрочем, один выход, который подсказывает старый и уродливый ростовщик. Он давно хотел взять в жены дочь купца, но девушка категорически не соглашалась, как не соглашается и сейчас, во время решительного объяснения не соглашается, хотя отец вот-вот окажется в долговой яме.

Отец, девушка и ростовщик беседуют на усыпанной гравием дорожке в саду. Ростовщик будто немного смягчился. Он не требует обязательного замужества в обмен на отказ от долга и готов решить вопрос жребием.

"Вот что, любезная, - говорит ростовщик девушке, - я подниму сейчас с дорожки два камешка - черный и белый, и положу их в свой цилиндр. А вы, не глядя, вытащите один из камней. Если вам достанется белый, я тотчас прощу вашему отцу долг и не стану больше домогаться вашей руки и сердца. А если достанется черный камешек, тогда вы войдете хозяйкой в мой дом, а ваш отец получит от меня новый заем. Согласны вы положиться на судьбу?" - "Согласна", - отвечает отважная английская девушка.

Ростовщик нагибается, проворно берет с дорожки два камня и бросает их в цилиндр. Но девушка успевает заметить, что оба камня черные, оба черные... Он ее обманывает, подлый ростовщик, он навязывает ей ненавистный брак!

Уродливый старик как ни в чем не бывало протягивает ей цилиндр: "Сделайте свой выбор!"

Как поступить девушке?

Дорогие читательницы, попробуйте стать на место юной англичанки, на ту же дорожку в саду и решить ее проблему. У вас был один план: подчиниться жребию, но гнусный ростовщик поломал этот план. Надо срочно придумать другой, спасительный. Надо изобрести, как избавиться от домогательств злодея. Только быстро, время не ждет, ростовщик уже протягивает свой цилиндр, размышлять некогда, надо действовать...

Если вы отыскали новый план, честь вам и хвала. А если нет, очень жаль, придется идти за ростовщика замуж. Впрочем, у гнусного старика окажется много невест: примерно треть девушек, участвовавших в этом психологическом эксперименте, не смогли перехитрить старика.

Нашей жизни теоремы

Эксперименты проводили в МГУ О. Тихомиров и его ученица Т. Корнилова. Некоторые девушки заявляли, что здесь и решать нечего: оба камня черные, какой ни вытащишь, все равно с ростовщиком под венец. Они были бессильны найти новый план в изменившейся ситуации.

Когда мы говорим о передаче вычислительной машине способности человека к планированию, следует указать, о каком человеке идет речь. О том ли, который ничего, кроме восклицаний "Это же надо!" и "Бедняжка!", не сумел произнести, или о том, который придумал спасительный план.

Быстрая умом купеческая дочка когда-то блестяще вышла из, казалось, безвыходного положения. Она не нарушила уговор - протянула руку и вытащила камешек из цилиндра, зажав его в кулачке. Потом бессильно опустила руку и разжала ладонь. Камень упал на гравийную дорожку и мгновенно слился с подобными ему камнями.

"Ах, - сказала девушка ростовщику, - от волнения я уронила свой камень! Какая жалость! Но все поправимо, ведь в цилиндре остался другой... Если оставшийся камень белый, значит, мне суждено стать вашей женой, а если черный..."

И девушка велела ростовщику подать ей другой камень, и оторопевший ростовщик выполнил ее приказ, и камень оказался черным, иначе и быть не могло.

Девушка получила свободу, а ее отец навсегда избавился от тягостного долга.

Понравилось вам решение девушки?

Уверен, что понравилось. Как ловко сумела она расширить условия задачи! Не ограничилась цилиндром с двумя роковыми камнями, а посмотрела мимо цилиндра, на дорожку сада, где было много камней - и белых и черных.

Она подумала: "У меня только одна возможность - вытащить черный камень. Достану я его, и что с ним делать? Куда девать.? Выбросить прочь? Но ростовщик это заметит и заставит идти замуж... А если незаметно выбросить? Тогда роковой камень смешается с обыкновенными на дорожке. И затеряется. В цилиндре, правда, останется другой черный камень. По уговору он выпал старику. Это его несчастье, а не мое... Если ему выпал черный камень, значит, мой, тот, который я, скажем, от волнения обронила... тот был белым! Прекрасно, спасительный выход найден, держись, старый скряга!"

Так, вероятно, думала девушка. Искинт так думать не может, хоть веди он анализ целей и средств, хоть доказывай он теоремы. Потому что Искинт не обучен расширять условия задач, потому что все его представление о мире ограничено заданными машине условиями.

В следующей главе мы узнаем о попытках погрузить Искинт в многоцветный и многотрудный внешний мир. А в этой главе только и осталось, что устроить четвертую свадьбу.

Вы догадываетесь, конечно, что у находчивой английской девушки был жених, капитан корабля, на снаряжение которого ее отец истратил свои и чужие деньги. Корабль уплыл в Индию, минули все сроки, а он не возвращался. Тут-то и явился ростовщик со своими претензиями, но был посрамлен.

Корабль, потрепанный штормами, вошел в устье Темзы лишь следующим летом. Девушка встречала своего капитана на набережной. Он подбежал к ней, поцеловал и сказал, что любит девушку гораздо сильнее, чем раньше.

Потом они бродили по городу, и девушка рассказывала о домогательствах ростовщика, а капитан - о своих приключениях и о Спинозе, чьи книги он читал в затяжные периоды штилей. Он цитировал наизусть многие теоремы философа, среди них вот эту:

"Ненависть увеличивается вследствие взаимной ненависти, и, наоборот, может быть уничтожена любовью".

Капитан говорил еще о том, как непросты и неоднозначны теоремы нашей жизни, как трудно даются правильные решения и как хорошо будет им вдвоем после свадьбы.

Чтобы вы, уважаемые читатели, не думали, что автор сочинил эту историю, я назову вам имена жениха и невесты. Его звали Джон, а ее Мэри.