§ 11. Циклы и исполнители алгоритмов

Итак, вы познакомились с новой формой организации действий - циклом. Естественно, что и наши знакомые - исполнители ВЫЧИСЛИТЕЛЬ и ЧЕРТЕЖНИК - владеют этой замечательной формой. Начнем с ЧЕРТЕЖНИКА. Составим для него алгоритм, выполнив который он окажется у края листа, независимо от своего начального положения:

 Пока впереди не край, повторять: 
 Прыгнуть. 
 Конец цикла.

А вот как с помощью циклов можно записать алгоритм решения задачи, разобранной в конце § 8 (отход на один шаг от края):

 Пока впереди не край, повторять: 
 Налево. 
 Конец цикла. 
 Налево. 
 Налево. 
 Прыгнуть.

А теперь займемся ВЫЧИСЛИТЕЛЕМ. Допустим, требуется найти и сообщить все положительные члены арифметической прогрессии с первым членом 10 и разностью - ?. Алгоритм будет выглядеть так:

 Присвоить а значение 10. 
 Присвоить d значение - 1/3. 
 Пока а>0, повторять: Сообщить а. 
 Присвоить а значение a + d. 
 Конец цикла.

В языке Бейсик цикл "пока" в зависимости от реализации на ЭВМ оформляется одним из двух способов:

 10 WHILE <условие> 
 20 <действие> 
 30 <действие> 
 90 <действие> 
 100 WEND 
 110 ...

 10 IF NOT <условие> THEN 110 
 20 <действие> 
 30 <действие> 
 90 <действие> 
 100 GOTO 10 
 110 ...

Следующую задачу можно назвать "экологической".

Задача. Расположенный на берегу реки металлургический завод осуществил сброс сточных вод, в результате чего концентрация вредных веществ в реке резко увеличилась. С течением времени эта концентрация, естественно, уменьшается. Требуется сообщить, каков будет уровень загрязнения реки через сутки, двое суток и т. д., до тех пор, пока концентрация не станет меньше предельно допустимой.

Экология...

Сначала построим математическую модель изучаемого явления. Специалистами-экологами установлена следующая приближенная закономерность: в каждом конкретном случае можно указать такое число К > 1, что концентрация примесей С уменьшается в К раз за сутки. При этом коэффициент К зависит от района, где протекает река, типа примесей и т. п. Значение К можно узнать из соответствующего справочника. Эту закономерность мы примем в качестве исходного предположения для нашей математической модели.

Исходными данными будут начальная концентрация С вредных веществ в реке, предельно допустимая концентрация D и коэффициент K. Результат - последовательность значений концентрации вредных веществ через сутки, двое суток и т. д. Связь между исходными данными и результатом дается следующими соотношениями:

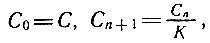
где С_n - концентрация вредных веществ через n суток после сброса.

Руководствуясь этой математической моделью, составим алгоритм решения задачи:

 Запросить начальное значение концентрации С, предельно допустимую концентрацию D и коэффициент 0. 
 Присвоить номеру суток п значение 0. Пока C>D, повторять: 
 Присвоить номеру суток п значение n + 1. 
 Присвоить концентрации С значение C/К 
 Сообщить "Номер суток; концентрация:" 
 Сообщить n, С. 
 Конец цикла.

Во время лабораторной работы 4 вы убедитесь, что первоначальное качество воды, как правило, восстанавливается годами.

Задания для самостоятельного выполнения

1. Что нарисует ЧЕРТЕЖНИК, выполнив следующий алгоритм из исходных положений, показанных на рисунке 20?

 Пока впереди край, повторять: 
 Повернуть налево. 
 Конец цикла. 
 Сделать шаг. 
 Пока впереди край, повторять: 
 Повернуть налево. 
 Конец цикла. 
 Сделать шаг.

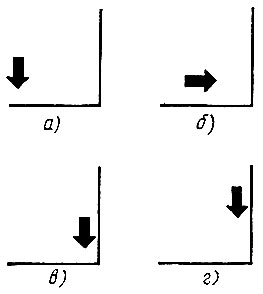
Рис. 20. Алгоритм исходных положений

Нарисуйте блок-схему этого алгоритма.

2. Сократите запись решений задач 3, б-3, д к § 8, используя циклы.

3°. Составьте алгоритм, выполнив который ЧЕРТЕЖНИК дойдет до угла листа, независимо от того, где он находился вначале.

4°. ЧЕРТЕЖНИК находится у края листа, но не в углу. Составьте алгоритм, выполнив который он нарисует прямоугольную рамку, отстоящую от края на расстоянии одного шага. (Указание: воспользуйтесь решением задачи 3.)

5. ЧЕРТЕЖНИК находится в углу листа. Составьте алгоритм, выполнив который он окажется в противоположном углу листа.

6°. ЧЕРТЕЖНИК находится в углу листа бумаги. Составьте алгоритм, выполнив который ЧЕРТЕЖНИК разлинует лист на полосы шириной 1 см.

7. Чему будут равны а и b после выполнения ВЫЧИСЛИТЕЛЕМ каждого из следующих - алгоритмов? Сколько раз будет выполняться тело цикла в каждом из них?

а)

 Присвоить а значение -5. 
 Присвоить b значение -2. 
 Пока a + b<ab, повторять: 
 Присвоить а значение 2а. 
 Присвоить b значение b + 1. 
 Конец цикла.

б)

 Присвоить а значение 25. 
 Присвоить b значение 1. 
 Пока а - b>а/b, повторять: 
 Присвоить а значение а +10. 
 Присвоить b значение -3b. 
 Конец цикла.

в)

 Присвоить а значение -3. 
 Присвоить b значение -1. 
 Пока а<b, повторять: 
 Если b<3, то: 
 Присвоить а значение а - b. 
 Присвоить b значение b + 2. 
 Иначе: 
 Присвоить а значение а + 2. 
 Присвоить b значение b - а. 
 Конец ветвления. 
 Конец цикла.

8. В алгоритме нахождения суммы квадратов первых ста чисел злоумышленник поменял местами несколько строк. Вот как выглядит его алгоритм:

 Присвоить S значение 0. 
 Пока I≤100, повторять: 
 Присвоить I значение 1. 
 Присвоить S значение S + I2. 
 Присвоить I значение I + 1. 
 Сообщить "Я нашел сумму. Вот она:". 
 Сообщить S. 
 Конец цикла.

Сколько раз будет ВЫЧИСЛИТЕЛЬ повторять тело цикла в этом алгоритме? Устраните путаницу в строках.

9°. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм нахождения суммы чисел, обратных квадратам первых 100 натуральных чисел.

10°. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм, пользуясь которым он запросит последовательно N чисел и сообщит их среднее арифметическое.

11°. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм нахождения остатка от деления одного натурального числа на другое.

12°. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм, пользуясь которым он запросит у нас последовательность из 10 чисел и определит, является ли она:

а) арифметической прогрессией;

б) геометрической прогрессией.

13°. Последовательность а_n строится так:

для каждого n>2. Составьте для ВЫЧИСЛИТЕЛЯ следующие алгоритмы:

а) алгоритм нахождения первого элемента последовательности, большего 1000;

б) алгоритм нахождения суммы первых 15 членов этой последовательности;

в) алгоритм нахождения первых десяти положительных членов этой последовательности;

г) алгоритм нахождения наибольшего из первых 20 членов последовательности.

14°. Леспромхоз ведет заготовку деловой древесины. Ее первоначальный объем на территории леспромхоза был равен 120000 м³. Ежегодный естественный прирост составляет 5,5%. Годовой план заготовки древесины - 9500 м³. Какой объем деловой древесины на данной территории будет через год, через два года и т. д.- до тех пор, пока этот объем не станет меньше минимально допустимого значения (23000 м³)? Составьте математическую модель для этой задачи и алгоритм ее решения.

15. а) В киоск "Мороженое" завезли неограниченное количество мороженого по 10 к. (молочное). Составьте математическую модель и алгоритм (для ВЫЧИСЛИТЕЛЯ) обслуживания очереди продавщицей мороженого.

б) На уроке математики учитель захотел проверить, хорошо ли ученики усвоили таблицу умножения. Составьте математическую модель и алгоритм (для ВЫЧИСЛИТЕЛЯ) опроса всех учеников класса. (Указание: воспользуйтесь решением задачи 7 к параграфу 9.)