§ 14. Вспомогательные алгоритмы и исполнители алгоритмов

Давайте составим для ЧЕРТЕЖНИКА алгоритм изображения знакомой нам фигуры - "креста" (см. задачу 2, § 6), используя вспомогательный алгоритм (начальное положение ЧЕРТЕЖНИКА обозначено на рис. 25). Очевидно, заданная фигура состоит из четырех элементов, изображенных на рисунке 26. Действия, которые должен выполнить ЧЕРТЕЖНИК, чтобы нарисовать этот элемент (начальное положение - как на рис. 26), запишем в виде вспомогательного алгоритма "Скобка":

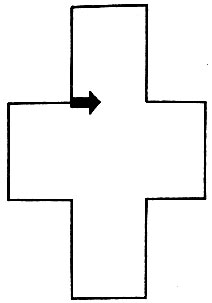
Рис. 25. Фигура креста

Рис. 26. Начало положения

 Алгоритм "Скобка". 
 Повернуть налево. 
 Повернуть налево. 
 Сделать шаг. 
 Повернуть налево. 
 Сделать шаг. 
 Повернуть налево. 
 Сделать шаг.

Теперь можно составить основной алгоритм:

 Выполнить алгоритм "Скобка". 
 Повернуть налево. 
 Выполнить алгоритм "Скобка". 
 Повернуть налево. 
 Выполнить алгоритм "Скобка". 
 Повернуть налево. 
 Выполнить алгоритм "Скобка".

Можно сказать, что мы "научили" ЧЕРТЕЖНИКА совершать овое для него действие: рисовать скобку "[". И теперь это ействие можно использовать для изображения не только данного, но и многих других рисунков.

Поработаем теперь с ВЫЧИСЛИТЕЛЕМ. Ранее мы составили для него алгоритм нахождения наибольшего из двух чисел. Давайте составим для ВЫЧИСЛИТЕЛЯ алгоритм нахождения наибольшего из трех чисел, скажем, а, b и с. План наших действий может быть, например, таким: сначала найдем наибольшее из чисел а и b, обозначив результат буквой z, а затем найдем наибольшее из чисел z и с. Мы видим, что здесь дважды выполняется алгоритм нахождения наибольшего из двух чисел, каждый раз различных, поэтому естественно записать вспомогательный алгоритм нахождения наибольшего из произвольных двух чисел, скажем, х и у, а затем его дважды использовать. Назовем этот алгоритм "Поиск максимума из двух чисел".

 Алгоритм "Поиск максимума из двух чисел". 
 Аргументы: числа х, у. 
 Результат: z (максимум из чисел х и у). 
 Если х>у, то: 
 Присвоить z значение х. 
 Иначе: 
 Присвоить z значение y. 
 Конец ветвления.

Алгоритм поиска наибольшего из трех чисел можно теперь записать так:

 Запросить а, b, с. 
 Выполнить алгоритм "Поиск максимума из двух чисел" при 
 х = а, у = b. 
 Выполнить алгоритм "Поиск максимума из двух чисел" при 
 x = z, у = с. 
 Сообщить z.

Как же ВЫЧИСЛИТЕЛЬ будет выполнять этот алгоритм? Сначала он запросит у нас три числа и обозначит их буквами а, b, с. После этого он выполнит вспомогательный алгоритм "Поиск...", взяв в качестве х число а, а в качестве у число b. Найдя максимум z, он еще раз выполнит вспомогательный алгоритм "Поиск...", взяв на этот раз в качестве х число г, в качестве у число с и обозначив результат буквой z. Это число z ВЫЧИСЛИТЕЛЬ сообщит нам.

Чтобы подготовиться к лабораторной работе 6, разберем следующую задачу.

Задача. Две моторные лодки равномерно двигались по реке в направлении к озеру, в которое река впадает. Поравнявшись, они начали двигаться равноускоренно. Какая из лодок раньше дойдет до озера?

Моторные лодки

Построение модели, как обычно, начнем с предположений, поскольку вряд ли нам удастся получить очень точные сведения о лодках (их исходных положениях, скоростях, ускорениях...), модель построим попроще. Лодки будем считать точками, реку и движение лодок - прямолинейными. Исходными данными являются начальные скорости лодок (обозначим их р и q), ускорения лодок (d u e), расстояние до озера (S). Результатом является сообщение, какая лодка раньше дойдет до озера или что лодки придут одновременно. Для определения этого надо найти, за какое время каждая лодка дойдет до озера, и сравнить получившиеся значения.

Время t находится из квадратного уравнения

где v - начальная скорость, а - ускорение, S - пройденный путь. По условию задачи скорости и ускорения обеих лодок положительны.

Для нахождения корней этого квадратного уравнения воспользуемся вспомогательным алгоритмом "РЕКВУР". Правда, он был предназначен для человека и в нем использованы обозначения x₁ и х₂. ВЫЧИСЛИТЕЛЬ таких обозначений "не понимает". Поэтому заменим их на х и у.

Поскольку скорости и ускорения положительны, лодки обязательно доплывут до озера. Поэтому наше квадратное уравнение имеет два корня (кстати, и дискриминант у него положителен; проверьте!). Какой же из корней выбрать?

Давайте рассуждать. Произведение корней отрицательно (проверьте, воспользовавшись теоремой Виета). Поэтому один из корней положительный, а другой - отрицательный. Отрицательный корень никакого физического смысла не имеет - ведь время движения лодок до озера не может быть меньше нуля. Значит, в качестве t надо взять положительный корень.

Вот теперь, когда мы окончательно разобрались (как нам кажется) в модели, напишем алгоритм решения задачи. В нем через Т обозначено время движения первой лодки, а через Z - второй.

 Сообщить "Введите расстояние до озера". 
 Запросить расстояние до озера S. 
 Сообщить "Введите начальные скорости лодок". 
 Запросить скорости лодок р и q. 
 Сообщить "Введите ускорения лодок". 
 Запросить ускорения лодок d u e. 
 Выполнить алгоритм "РЕКВУР", взяв в качестве аргументов d/2, р и -S. 
 Если корень х>0, то: 
 Присвоить времени Т движения первой лодки значение х. 
 Иначе: 
 Присвоить времени Т движения первой лодки значение у. 
 Конец ветвления. 
 Выполнить алгоритм "РЕКВУР", взяв в качестве аргументов е/2, q и -S. 
 Если корень х>0, то: 
 Присвоить времени Z движения второй лодки значение х. 
 Иначе: 
 Присвоить времени Z движения второй лодки значение у. 
 Конец ветвления. 
 Если T<Z, то: 
 Сообщить "Первой пришла лодка номер 1". 
 Конец ветвления. 
 Если T>Z, то: 
 Сообщить "Первой пришла лодка номер 2". 
 Конец ветвления. 
 Если T = Z, то: 
 Сообщить "Лодки пришли одновременно". 
 Конец ветвления.

В этом алгоритме мы не стали учитывать естественные ограничения на скорости, ускорения и расстояние до озера. Подумайте, каковы эти ограничения, и добавьте соответствующую проверку в алгоритм.

В языке Бейсик вспомогательные алгоритмы оформляются следующим образом. Перед заголовком ставится слово REM (от английского remark - пояснение). Например,

После заголовка записывается сам вспомогательный алгоритм. В конце обязательно пишется слово RETURN (возвратиться).

Вспомогательные алгоритмы лучше размещать после основного алгоритма. Это означает, что номера строк вспомогательного алгоритма должны быть больше номеров строк основного алгоритма.

Прежде чем обратиться к вспомогательному алгоритму, надо присвоить аргументам этого алгоритма нужные значения, а затем написать команду GOSUB..., где вместо многоточия пишется номер первой строки вспомогательного алгоритма.

Например, алгоритм нахождения максимума из трех чисел на языке Бейсик выглядит так:

 10 INPUT А,В,С 
 20 LET X = A 
 30 LET Y = B 
 40 SOSUB 200 
 50 LET X = Z 
 60 LET Y = C 
 70 GOSUB 200 
 80 PRINT Z 
 90 STOP 
 200 REM Поиск максимума из двук чисел. Аргументы X,Y. Результат Z. 
 210 IF X>Y THEN LET Z = X ELSE LET Z = Y 
 220 RETURN

К сожалению, в языке Бейсик не предусмотрено "замораживание" значений переменных. Поэтому в нем нельзя использовать для обозначения переменных в тексте основной программы те буквы, которыми обозначены переменные в подпрограммах.

Задания для самостоятельного выполнения

1. Что нарисует ЧЕРТЕЖНИК на бесконечном листе бумаги, выполняя следующий алгоритм?

а)

 Выполнить алгоритм "Скобка". 
 Выполнить алгоритм "Скобка". 
 Выполнить алгоритм "Скобка".

б)

 Выполнить алгоритм "Скобка". 
 Повернуть налево. 
 Выполнить алгоритм "Скобка".

2. Во вспомогательном алгоритме "Скобка" злоумышленник стер две команды. В результате, выполнив приведенный

данном параграфе алгоритм рисования "креста", ЧЕРТЕЖНИК вместо рисунка 25 изобразил рисунок 27. Какие команды стер злоумышленник? 3°. Составьте для ЧЕРТЕЖНИКА вспомогательный алгоритм поворота направо. Используя этот вспомогательный алгоритм, составьте алгоритм рисования скобки, начиная с нижнего правого конца (рис. 28).

4. Пользуясь решением задачи 6 из §11, составьте для ЧЕРТЕЖНИКА алгоритм изображения на листе бумаги сетки из квадратов со стороной 1 см.

5. Составьте для ЧЕРТЕЖНИКА алгоритмы рисования фигур, изображенных на рисунке 29. Какой общий вспомогательный алгоритм естественно составить для рисования этих фигур?

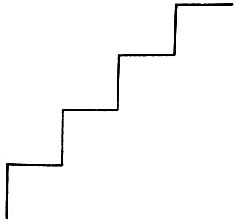
Рис. 27. Алгоритм рисования креста

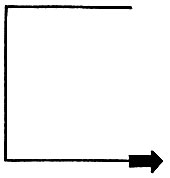
Рис. 28. Алгоритм рисования скобки

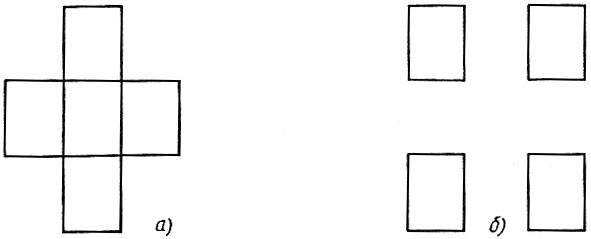
Рис. 29. Алгоритм рисования фигур

6. Чему будут равны переменные х, у, z после выполнения ВЫЧИСЛИТЕЛЕМ следующего алгоритма:

 Присвоить х значение 1. 
 Присвоить у значение 3. 
 Присвоить z значение 3. 
 Выполнить алгоритм "Поиск максимума из двух чисел" при х = ху, у = ух. 
 Выполнить алгоритм "Поиск максимума из двух чисел" при x = xz, y = zx. 
 Выполнить алгоритм "Поиск максимума из двух чисел" при х = уz, y = zy.

7 Пользуясь вспомогательным алгоритмом "Поиск максимума из двух чисел", составьте для ВЫЧИСЛИТЕЛЯ алгоритм нахождения максимального из четырех чисел.

8. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм решения уравнений вида

используя вспомогательный алгоритм решения квадратных уравнений.

9. В алгоритме решения задачи о двух лодках имеются два почти одинаковых блока действий. Найдите эти блоки и составьте соответствующий вспомогательный алгоритм.