§ 15. Задача о выборе места строительства железнодорожной станции

Помните, в поэме Н. А. Некрасова описано, как собрались мужики окрестных деревень обсудить, кому на Руси жить хорошо? В те бесправные времена они ничего не могли сделать, чтобы облегчить свою жизнь: все социальные вопросы за них решали хозяева. Теперь все иначе. Ни один социальный вопрос не может быть решен без широкого обсуждения. Вот одна из задач, с которыми часто приходится сталкиваться планирующим органам.

Выборе места

Задача. В одном районе расположены четыре населенных пункта. По территории района проходит железная дорога. По просьбе жителей района планируется построить железнодорожную станцию и проложить дороги от нее до каждого населенного пункта. Требуется определить наиболее удобное расположение железнодорожной станции.

Как всегда, начнем с построения математической модели. Прежде всего допустим, что участок дороги, проходящий по территории района, прямолинеен и в любом месте участка можно построить станцию и соединить ее прямолинейными дорогами с каждым населенным пунктом (рис. 30). Нарисуем оси координат а карте района так, чтобы ось абсцисс проходила по интересующему нас участку железной дороги, а начало координат совпадало с его левым концом.

Населенные пункты будем изображать кружочками, а названия позаимствуем у Некрасова (хотя, конечно, эти деревни давно переименованы).

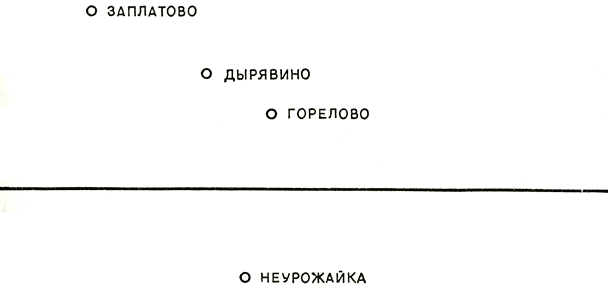
Рис. 30. Математическая модель

Теперь надо уяснить смысл слов "наиболее удобное расположение станции". Это можно понимать по-разному. Если стремиться к экономии средств на строительство дорог, то станцию надо расположить так, чтобы сумма длин дорог, соединяющих станцию с населенными пунктами, была наименьшей. Если же стремиться к максимальной справедливости, то место для станции надо выбрать так, чтобы наибольшее из расстояний от нее до населенных пунктов было как можно меньше. Например, если в самом дальнем от станции населенном пункте заболеет человек, то его надо доставить на станцию за самое короткое время.

На рисунке 31 кружочками обозначены два населенных пункта, буквами А и Б обозначены места, где надо строить станцию, руководствуясь соответственно первым и вторым толкованием слов "наибольшее удобство". Как видите, точки А и Б достаточно далеки друг от друга. Мы за справедливость (как и поэт-демократ Н. А. Некрасов). Поэтому изберем второй принцип.

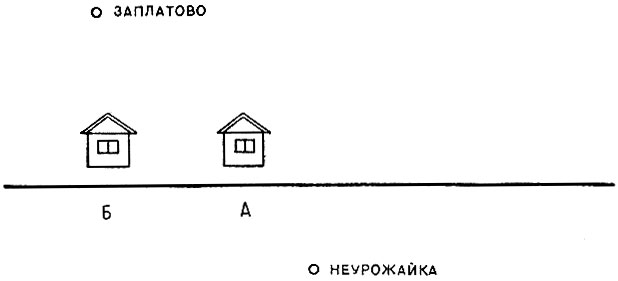
Рис. 31. Населенный пункт схематично

Определим исходные данные и результат для нашей математической модели. Исходными данными, конечно, являются координаты населенных пунктов и длина S отрезка, изображающего на карте участок железной дороги, пролегающий по району. Результат - абсцисса точки, где будет строиться станция.

Остается найти соотношения между результатом и исходными данными. Координаты наших четырех населенных пунктов обозначим (а, b), (с, d) (e, f) (g, h).

Возьмем любую точку на отрезке, изображающем железную дорогу. Пусть t - ее абсцисса. Через z обозначим максимальное из расстояний между этой точкой и каждым из населенных пунктов. Иначе говоря,

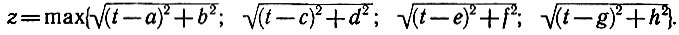
Чтобы определить, где построить станцию, надо узнать, при каком t из отрезка [0; S] переменная г принимает наименьшее значение. Как же найти это t? Ведь мы не можем перебрать все числа от 0 до S: их бесконечно много. Выход один - искать приближенное значение t. Для этого разобьем отрезок [0; S] на равные части, длину каждой из них обозначим буквой r. Затем найдем значения z при t = 0, r, 2r и так далее, пока t≤S. Выберем из этих значений наименьшее и определим, при каком t оно достигается. Это значение t будет отличаться от искомого результата не больше, чем на r. Поэтому мы возьмем его в качестве результата.

Вообще говоря, не для каждой функции полученное таким методом значение t действительно будет отстоять от точки минимума менее, чем на r (попробуйте привести пример такой функции). Однако можно строго доказать, что в данном случае то верно.

Итак, для решения задачи нам потребуется из достаточно большого количества чисел найти минимальное. Чтобы лучше понять, как это делать, представьте себе, что ваш класс в алфавитном порядке вызывают на медосмотр, а любознательный врач задался целью выявить самого легкого ученика. Скорее сего врач поступит так. Вызвав первого ученика, он запишет го вес и фамилию. Пригласив следующего, он сравнит его вес с записанным числом. Если этот ученик оказался легче, врач зачеркнет предыдущую запись и запишет сведения о новом ученике, в противном случае сохранится прежняя запись. Затем он вызовет следующего ученика, и так далее. Когда пройдет весь класс, на листке у врача останется фамилия и вес самого легкого ученика.

При решении нашей задачи мы будем поступать точно так же. роли учеников будут выступать значения t (то есть числа 0, r, 2r и т. д.), а взвешивание заменим вычислением числа z. Остается понять, что будет играть роль листка, на который врач записывал фамилию и вес ученика. Ведь ВЫЧИСЛИТЕЛЬ не умеет" пользоваться бумагой и ручкой. ВЫЧИСЛИТЕЛЬ моет "записать" (запомнить) число единственным способом - присвоить его какой-нибудь переменной. В нашем случае потребуются две переменные: придется запоминать числа t и z. Для запоминания t приспособим переменную V, а для запоминания z - временную М. По окончании выполнения алгоритма значение переменной V будет указывать искомое место расположения станции, а М - расстояние от этого места до самого удаленного из населенных пунктов.

Теперь мы можем полностью представить себе, что должен делать ВЫЧИСЛИТЕЛЬ, решая эту задачу. Сначала он положит t равным 0 и подсчитает r; это z он примет за начальное значение М, а 0 - за начальное значение V. Затем ВЫЧИСЛИТЕЛЬ подсчитает z при t = r и сравнит его с М. Если z окажется меньше М, он присвоит М это значение z, а V - значение t, в противном случае оставит М и V неизменными и т. д., пока не дойдет до значения t = S.

Ясно, что поиск z при данном t лучше всего оформить в виде вспомогательного алгоритма. Запишем этот алгоритм.

 Алгоритм "Нахождение максимального из расстояний до населенных пунктов". 
 Аргументы: а, b, с, d, е, f, g, h (координаты населенных пунктов) и t (координата точки на отрезке [0;S]). 
 Результат: z (максимальное из расстояний до населенных пунктов). 
 Выполнить алгоритм "Поиск максимума из двух чисел" при . 
 Выполнить алгоритм "Поиск максимума из двух чисел" при . 
 Выполнить алгоритм "Поиск максимума из двух чисел" при 

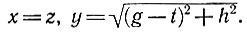
Основной алгоритм запишется так:

 Запросить координаты населенных пунктов а,b, c,d, е,f, g, h 
 Запросить длину S участка железнодорожного пути и длину r отрезка разбиения. 
 Присвоить координате t значение 0. 
 Выполнить алгоритм "Нахождение максимального из расстояний до населенных пунктов", взяв в качестве аргументов а,b, сd e,f, g,h и t. 
 Присвоить М начальное значение, равное z. 
 Присвоить координате V искомой точки начальное значение, равное t. 
 Пока t<S, повторять: 
 Присвоить t значение t + r. 
 Выполнить алгоритм "Нахождение максимального из расстояний до населенных пунктов", взяв в качестве аргументов а,b, c,d, e,f, g,h и t. Если z<M, то: 
 Присвоить М очередное значение, равное z. Присвоить V очередное значение, равное t. Конец ветвления. Конец цикла. 
 Сообщить "Координата искомой точки и максимальное расстояние от нее до населенных пунктов". Сообщить V, М.

Этот алгоритм позволяет найти решение задачи приближенно. Однако можно отыскать и точное решение этой задачи. Найдите его самостоятельно!

Задания для самостоятельного выполнения

1°. ЧЕРТЕЖНИК находится в углу квадратного листа бумаги. Составьте алгоритм рисования "лесенки", соединяющей начальное положение ЧЕРТЕЖНИКА с противоположным углом листа.

2°. ЧЕРТЕЖНИК находится в некоторой точке квадратного листа бумаги. Используя алгоритмы решений задачи 3 из § 11 и задачи 1 данного параграфа как вспомогательные, составьте алгоритм изображения лесенки на рисунке 32.

3. Чему будут равны переменные х, у после выполнения ВЫЧИСЛИТЕЛЕМ следующих алгоритмов:

а)

 Присвоить х значение 2. 
 Присвоить у значение 1. 
 Пока х>у, повторять: 
 Выполнить алгоритм "РЕКВУР" 
 при а = 1, b = х + у, с = ху. 
 Если k = 0, то: 
 Сообщить "Что-то не то! 
 Прекращаю работу". 
 Стоп. 
 Конец ветвления. 
 Присвоить х значение - х. 
 Конец цикла.

б)

 Присвоить и значение 2. 
 Присвоить v значение 1. 
 Пока u>v, повторять: 
 Выполнить алгоритм "РЕКВУР" 
 при а = 1, b = uv, c = u + v. 
 Если k = 0, то: 
 Присвоить и значение и+1. 
 Присвоить v значение v+1. 
 Иначе: 
 Присвоить и значение х. 
 Присвоить v значение у. 
 Конец ветвления. 
 Конец цикла.

в)

 Присвоить и значение 3. 
 Присвоить v значение 1. 
 Пока u>v, повторять: 
 Выполнить алгоритм "РЕКВУР" при a = 1, b = uv, c = u + v. 
 Выполнить алгоритм "Поиск максимума из двух чисел" 
 при x = k, у = 0,5. 
 Присвоить v значение v+z. 
 Конец цикла.

4°. Пользуясь алгоритмом для нахождения остатка от деления одного числа на другое (см. задачу 11 из § 11) как вспомогательным, составьте для ВЫЧИСЛИТЕЛЯ следующие алгоритмы:

а) алгоритм, позволяющий определить, делится ли одно число на другое;

б) алгоритм, позволяющий определить, является ли число степенью двойки;

в) алгоритм, позволяющий найти наименьший делитель данного числа (отличный от 1);

г) алгоритм, позволяющий определить, является ли число простым (число называется простым, если оно отлично от единицы и делится только на себя и на единицу);

д) алгоритм, позволяющий определить, является ли число совершенным (число называется совершенным, если оно равно сумме всех его делителей, отличных от него самого).

5. Составьте алгоритм нахождения площадей фигур методом Монте-Карло (см. § 12), в котором проверка того, что точка попала внутрь фигуры, была бы вспомогательным алгоритмом.

6°. Составьте математическую модель и алгоритм решения задачи о железнодорожной станции:

а) руководствуясь первым принципом выбора наиболее удобного расположения станции (минимум суммы расстояний);

б) руководствуясь компромиссным принципом: если z - расстояние от станции до наиболее удаленного пункта, a ω - сумма расстояний до всех пунктов, то требуется сделать как можно меньшим среднее арифметическое из z и ω.