§ 19. Задачи планирования

Представьте, что вас выбрали директором завода и вы, изучив спрос, решили организовать участок для производства двух видов товаров широкого потребления - мясорубки и скороварки. Для краткости обозначим эти товары буквами А и Б. Допустим, что вам удалось заключить договор со смежниками на поставку ресурсов (металла, электроэнергии и т. п.) и выделить определенное число рабочих. Чтобы обеспечить рентабельность участка, совет трудового коллектива установил план по реализации, указывающий минимальные объемы производства для каждого изделия. Всякий хороший директор стремится к тому, чтобы прибыль была наибольшей. Будем считать это и вашей задачей.

Прибыль

Задача. На участке работает 20 человек; каждый из них в среднем за год работает 1800 ч. Выделенные ресурсы: 32 т металла, 54 тыс. квт·ч электроэнергии. План по реализации: не менее 2 тыс. изделий А и не менее 3 тыс. изделий Б. На выпуск 1 тыс. изделий А затрачивается 3 т металла, 3 тыс. квт·ч электроэнергии и 3 тыс. ч рабочего времени. На выпуск 1 тыс. изделий Б затрачивается 1 т металла, 6 тыс. кВт·ч электроэнергии и 3 тыс. ч рабочего времени. От реализации 1 тыс. изделий А завод получает прибыль 5 тыс. р., от реализации 1 тыс. изделий В - 7 тыс. р. Выпуск какого количества изделий А и Б (в тыс. штук) надо запланировать, чтобы прибыль от их реализации была наибольшей?

Как вы помните, начать нужно с математической модели. Сделаем упрощающие предположения. Часть из них мы высказали уже при формулировке задачи: мы опустили целый ряд ограничений на ресурсы, необходимые для производства (кроме людских ресурсов, расхода металла и электроэнергии), а также взяли усредненное значение затрат рабочего времени.

Далее, пусть х - планируемое количество изделий А, а у - планируемое количество изделий Б (в тыс. штук). Для простоты будем считать числа х и у натуральными.

Все исходные данные указаны в условии задачи. Результатом, очевидно, являются максимальная возможная прибыль от реализации и соответствующие ей оптимальные значения х и у.

Запишем теперь математические соотношения, связывающие исходные данные и результаты.

План по реализации запишется следующими неравенствами:

Поскольку на изготовление изделия А расходуется 3 т металла, а на изготовление изделия Б - 1 т металла, общий расход металла составит 3x + y т. По условию, он не должен превышать 32 т, то есть должно быть справедливо неравенство:

Аналогично записываются остальные ограничения. Ограничение на расход электроэнергии:

Ограничение на ресурсы рабочего времени:

Прибыль от реализации х тыс. изделий А и у тыс. изделий Б равна

Теперь наша задача может быть сформулирована так: найти наибольшее значение выражения 5x + 7y (x, у - натуральные числа), где х и у должны удовлетворять неравенствам (1) - (5).

Приступим к составлению алгоритма.

Требуемые значения х и у мы будем искать, перебирая все значения, которые они могут принимать. Поскольку перебрать можно лишь конечное число значений, нужно, пользуясь неравенствами (1) - (5), найти наибольшие допустимые значения х и у. Из неравенств (3) - (5) получаем (вспомните правила действий с неравенствами):

Далее, поскольку х≥2, получаем:

Отсюда: у≤8. Рассуждая аналогично, из условия у≥3 получаем: x≤29/3, откуда х≤9 (мы рассматриваем только целые значения х и у!). Таким образом, для любых значений х от 1 до 9 и у от 1 до 8 можно подсчитать значение прибыли по формуле 5х + 7у, если, конечно, х и у удовлетворяют неравенствам (1) - (5). Если же х и у не удовлетворяют неравенствам (1) - (5), то значение прибыли будем считать равным нулю, поскольку в этом случае участок просто не в состоянии выпустить х тысяч изделий А и у тысяч изделий Б.

Полученные 72 значения прибыли удобно расположить в форме таблицы, состоящей из 9 строк и 8 столбцов. На пересечении строки с номером х и столбца с номером у записывается прибыль, полученная от реализации х тыс. изделий А и у тыс. изделий Б. Обозначим эту таблицу буквой V.

Итак, элементы таблицы V будем определять по формуле:

(6)

Таким образом, задача свелась к нахождению максимального элемента в таблице V. Подобную задачу мы разбирали на лабораторной работе 9. Единственное существенное отличие состоит в том, что таблица результатов наблюдений нам была дана заранее, а элементы таблицы V нужно предварительно сосчитать по приведенному выше правилу (6).

Проведем пошаговую детализацию алгоритма. Он будет состоять из следующих двух крупных блоков:

Пошаговая детализация алгоритма

В лабораторной работе 9 вы, по сути дела, составили программу нахождения максимального элемента в таблице. Вы можете пользоваться своим алгоритмом или, если хотите, приведенным ниже.

Сначала напишем вспомогательный алгоритм поиска максимума в строке (его аргументом является номер строки I, а результатом максимальное число R в строке таблицы и его номер Q в строке):

 Алгоритм "Максимальный элемент в строке". 
 Аргумент: I (номер строки). 
 Результаты: максимальное число R и его номер Q в строке. 
 Присвоить R начальное значение 0. 
 Для каждого J от 1 до 8: 
 Если V (I, J)>R, то: 
 Присвоить R очередное значение V (I, J). 
 Присвоить Q очередное значение J. 
 Конец ветвления. 
 Конец цикла по J.

Алгоритм поиска максимума в таблице выглядит так:

 Присвоить М начальное значение 0. 
 Для каждого Р от 1 до 9: 
 Выполнить алгоритм "Максимальный элемент в строке", взяв I равным Р. 
 Если R>M, то: 
 Присвоить М очередное значение, равное R. 
 Присвоить X очередное значение, равное Р. 
 Присвоить У очередное значение, равное Q. 
 Конец ветвления. 
 Конец цикла по Р. 
 Сообщить "Максимум прибыли, количество изделий А, количество изделий Б (тыс. штук)". 
 Сообщить М, X, У.

Теперь составим алгоритм, реализующий первый блок. Ясно, что этот алгоритм состоит в вычислении для всех х от 1 до 9 и всех у от 1 до 8 значения V (х, у). Вычисление V (х, у) можно изобразить блок-схемой (рис. 40).

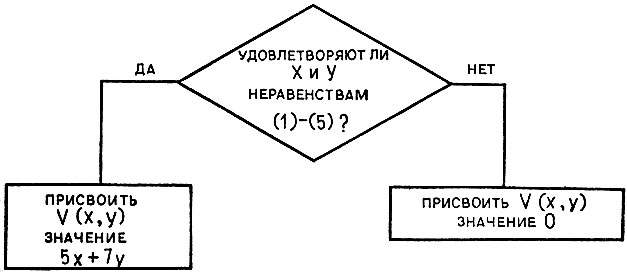
Рис. 40. Блок-схема

В дальнейшей детализации нуждается лишь проверка условия. Соответствующий вспомогательный алгоритм назовем "Условие"; его аргументы - х и у, а результат - сигнальная переменная С: она равна 0, если условие выполняется, и равна 1 в противном случае. Этот алгоритм выполняется так: сначала С присваивается значение 0; затем если хотя бы одно из пяти неравенств (1) - (5) нарушается, то С становится равным 1, в противном случае - остается равным 0.

 Алгоритм "Условие". 
 Аргументы: X, У (количество изделий А и Б). 
 Результат: С (сигнальная переменная, равная 0, если X и У удовлетворяют неравенствам (1) - (5), и равная 1 в противном случае). 
 Присвоить С начальное значение 0. 
 Если Х<2, то: 
 Присвоить С значение 1. 
 Конец ветвления. 
 Если Y<3, то: 
 Присвоить С значение 1. 
 Конец ветвления. 
 Если 3Х + Y>32, то: 
 Присвоить С значение 1. 
 Конец ветвления. 
 Если 3Х + 6Y>54, то: 
 Присвоить С значение 1. 
 Конец ветвления. 
 Если 3Х + 3Y>36, то: 
 Присвоить С значение 1. 
 Конец ветвления.

Как видите, алгоритм получился довольно длинный и однообразный. У каждого уважающего себя программиста должно возникнуть желание сделать его покороче. Да и нет никакой гарантии, что плановый отдел не предъявит завтра еще какие-нибудь новые условия. Что же тогда, весь алгоритм переписывать? Разумеется, надо всегда стремиться к тому, чтобы текст вспомогательного алгоритма не зависел от данных, которые требуются в основном алгоритме. Решить обе поставленные задачи нам снова поможет табличная организация данных. Только сначала превратим неравенства (1) - (5) в неравенства одного смысла. Для этого достаточно заменить неравенства x≥2 И y≥3 на неравенства -х≤-2и -у≤-3. Составим из коэффициентов при х и у и правых частей неравенств таблицу Т:

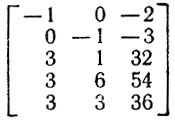
Теперь вспомогательный алгоритм "Условие" можно записать так:

 Алгоритм "Условие". 
 Аргументы: X, Y. 
 Результат: С. 
 Присвоить С значение 0. 
 Для каждого I от 1 до 5: 
 Если T (I, 1) x X + T(I,2) x Y>T(I,3), то: 
 Присвоить С значение 1. 
 Конец ветвления. 
 Конец цикла по I.

Как видите, алгоритм получился гораздо короче и универсальнее: при изменении исходных данных не надо переписывать весь алгоритм, а достаточно поменять таблицу Т и, если число условий изменится, поменять число 5 в цикле "Для каждого". Теперь мы можем записать основной алгоритм решения задачи:

 Для каждого I от 1 до 9: 
 Для каждого J от 1 до 8: 
 Выполнить алгоритм "Условие" при Х = J, Y = J. 
 Если С = 0, то: 
 Присвоить V(I, J) значение прибыли 5I + 7J. 
 Иначе: 
 Присвоить V (I, J) значение 0. 
 Конец ветвления. 
 Конец цикла по J. 
 Конец цикла по I. 
 Присвоить М начальное значение 0. 
 Для каждого Р от 1 до 9: 
 Выполнить алгоритм "Максимальный элемент в строке", взяв I равным Р. 
 Если R>M, то: 
 Присвоить М очередное значение, равное R. 
 Присвоить X очередное значение, равное Р. 
 Присвоить Y очередное значение, равное Q. 
 Конец ветвления. Конец цикла по Р. 
 Сообщить "Максимум прибыли, количество изделий А, количество изделий Б (тыс. штук)". 
 Сообщить М, X, У.

Соответствующая программа на языке Бейсик:

 1 DIH V(9,8) 
 2 FOR I = l TO 9 
 3 FOR J = 1 TO 8 
 4 LET X = I: LET Y =J: GQSUB 22 
 3 IF C = 0 THEN LET V(I,J) = 5*I + 7*J ELSE LET V(I,J) = 0 
 6 NEXT J 
 7 NEXT I 
 8 LET H = 0 
 9 FOR P = l TO 9 
 10 LET I = P : GQSUB 16 
 11 IF R>M THEN LET M = R1 LET X = P1 LET Y = 0 
 12 NEXT P 
 13 PRINT "Максимум прибыли, планируемый выпуск изделий А и Б (тыс. штук)" 
 14 PRINT M,X,Y 
 15 STOP 
 16 REM Максимальный элемент в строке 
 17 LET R = Q 
 18 FOR J = 1 TO 8 
 19 IF V(I,J)>R THEN LET R=V(I,J) : LET Q = J 
 20 NEXT J 
 21 RETURN 
 22 REM Условие 
 23 LET С = 0 
 24 IF X<2 THEN LET C = l 
 25 IF Y<3 THEN LET C = l 
 26 IF 3∗X + Y>32 THEN LET C = l 
 27 IF 3∗X + 6∗Y>54 THEN LET C = l 
 28 IF 3∗X + 3∗Y>36 THEN LET C = l 
 29 RETURN

Задания для самостоятельного выполнения

1°. Составьте алгоритм нахождения максимального значения выражения 5x² - 6у², если натуральные числа х, у удовлетворяют неравенствам: х - 2у<4, 2ху>7, x + y<100.

2°. Кооператив из 20 человек выпускает изделия А и Б, те же, что и участок завода, о котором рассказано в этом параграфе. Кооператив намерен получить прибыль не менее 65 тыс. р. в год. Ему выделены 54 тыс. кВт"ч электроэнергии. Какое минимальное количество металла потребуется кооперативу, чтобы обеспечить нужную прибыль? Составьте математическую модель и алгоритм решения этой задачи.

3°. Для полива трех полей колхоз использует насосную станцию. На первое поле требуется подать не менее 200 кубометров воды в сутки, на второе - не менее 300, на третье - не менее 350. В распоряжении колхоза 1200 кубометров воды в сутки. Стоимость подачи q кубометров воды на первое поле 15q^1/8 р., на второе поле 17,2q^1/8 р., на третье 19q^1/8 р. Сколько кубометров воды надо подать на каждое поле, чтобы затраты были наименьшими? Составьте математическую модель и алгоритм решения этой задачи.