§ 22. Циклы в языке Бейсик

Цикл "Пока" мы записывали в следующем виде:

 Пока Q, повторять: 
 Р 
 Конец цикла.

Здесь Q - условие, Р - последовательность действий, которую надо выполнять, пока истинно условие Q.

В языке Бейсик цикл "Пока" в зависимости от реализации на ЭВМ оформляется одним из двух способов:

 10 WHILE <условие> 
 20 Р 
 30 WEND 
 40 ...

 10 IF NOT <условие> THEN 40 
 20 Р 
 30 GOTO 10 
 40 ...

В первом варианте слово "пока" заменяется на WHILE, слово "повторять" опускается, слова "конец цикла" заменяются на WEND. Нетрудно проверить, что, выполняя последовательность команд из второго варианта, ЭВМ будет повторять действия из последовательности Р до тех пор, пока условие Q истинно.

Посмотрите на следующем примере, как выглядит такой перевод:

Алгоритм

 Запросить a, b. 
 Присвоить n значение 0. 
 Пока а < b, повторять: 
 Присвоить п значение n + 1. 
 Сообщить "Значения а, n". 
 Сообщить а, n. 
 Конец цикла.

Программа на Бейсике

 10 INPUT А, В 
 20 N"0 
 30 IF A> = B THEM 90 
 40 A = 10*A 
 50 N = N + 1 
 60 PRINT "Значении A, N" 
 70 PRINT A,N 
 80 GOTO 30 
 90 END

Подумайте: для решения какой задачи предназначен этот алгоритм?

Теперь - о цикле "Для каждого". Вот его запись:

 Для каждого I от L до R: 
 Р 
 Конец цикла по I

(Напомним: I - "счетчик" цикла, L - начальное значение "счетчика", R - конечное значение "счетчика", Р - тело цикла.) В языке Бейсик цикл "Для каждого" оформляется так:

 10 FOR I = L TO R 
 20 Р 
 30 NEXT I

(т. е. слова "Для каждого" заменяются на FOR, "от" - на знак равенства, "до" - на ТО, "конец цикла по" на NEXT).

Составим программу, выполняя которую ЭВМ напечатает кубы целых чисел от 10 до 100.

 10 FOR Х = 10 ТО 100 
 20 PRINT Х^3 
 30 NEXT X 
 40 END

Как обычно, завершим параграф подготовкой к лабораторной работе: решим задачу на закон Архимеда.

Задача. В ванне на поверхности воды плавает деревянный шар. Какова высота части шара, находящейся под водой?

В ванне

Как всегда, начнем с упрощающих предположений. Будем считать, что шар однороден и имеет идеально сферическую форму, поверхность воды - плоскость, плотность воды равна 1 г/см³ . Исходные данные - радиус шара R и масса М. Результат - высота h подводной части шара. Соотношение между исходными данными и результатами дает нам закон Архимеда. Поскольку тело спокойно плавает, действующая на него сила тяжести уравновешена выталкивающей силой. Значит, масса шара равна массе воды, вытесненной им. Масса вытесненной воды равна объему подводной части шара, умноженному на плотность воды. Осталось подсчитать объем подводной части шара. Высота ее равна Л. Заглянув в справочник, вы без труда найдете нужную формулу (в конце одиннадцатого класса вам придется ее выучить наизусть, так что начинайте учить заранее): объем шарового сегмента высоты h равен 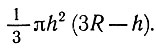. Вот мы и получили искомое соотношение:

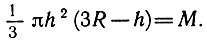(1)

Раскрыв скобки и перенеся все в правую часть, получим:

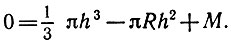
Как видите, наша физическая задача свелась к решению кубического уравнения относительно h. Ваших знаний по математике, наверно, недостаточно, чтобы найти h с приемлемой точностью. А с помощью ЭВМ вы легко сможете это сделать.

Нам будет удобнее решать уравнение (1), поскольку ясен его физический смысл: справа - масса шара, слева - масса вытесненной воды. Прежде всего заметим, что h>0 и h<2R. Если в левую часть уравнения (1) подставить h = 0, то она станет равна 0, т. е. меньше М. А что если подставить h = 2R? Слева получится 4/3 πR³. Как это число соотносится с М? Математика здесь ничего нам подсказать не может, поэтому обратимся к физическим соображениям. Высота h станет равной 2R, если шар целиком погрузить под воду. Но в этом случае выталкивающая сила больше силы тяжести шара! Значит, и масса вытесненной воды больше массы шара. Итак, если h = 2R, то М должно быть меньше

.

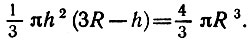
Поиск h можно уподобить стрельбе по цели. Ведь мы хотим найти такое h, чтобы "попасть" в число М. При h = 0 получился "недолет"; при h = 2R - "перелет". Видите, мы взяли число М в "вилку"! Что делать дальше - вы уже знаете по лабораторной работе 11. Надо брать середину отрезка [0; 2R], вычислять значение левой части, смотреть, получился "перелет" или "недолет", определять новую "вилку" и т. д., пока h не будет найдено с требуемой точностью, скажем, до тысячных. Но на лабораторной работе 11 вы делали это вручную (машина только вела "стрельбу"), а теперь мы этот процесс автоматизируем.

Для этого обозначим через А и В концы "вилки": сначала они равны соответственно 0 и 2R, а потом будут меняться. Серединой отрезка [А; В] служит число (А + В)/2. Если, взяв это число в качестве h, мы получим "недолет", сдвинем левую границу "вилки", положив А равным h, в противном случае сдвинем правую границу "вилки", положив В равным h. Будем продолжать действовать таким образом, пока границы "вилки" не будут отстоять друг от друга меньше чем на 0,001. Запишем алгоритм:

 Сообщить "Введите радиус и массу шара". 
 Запросить R, М. 
 Присвоить А значение 0. 
 Присвоить В значение 2R. 
 Пока В - А > 0,001, повторять: 
 Присвоить h значение (A+В)/2. 
 Если  то: 
 Присвоить А значение h. 
 Иначе: 
 Присвоить В значение h. 
 Конец ветвления. 
 Конец цикла. 
 Сообщить "Величина h равна". 
 Сообщить h.

А его перевод на язык Бейсик сделайте, пожалуйста, сами.

Вопросы

1. Как оформляется на Бейсике цикл "Пока"?

2. Как оформляется на Бейсике цикл "Для каждого"?

3. Какую роль играет команда NEXT?

4. В чем состоит метод деления пополам?

Задания для самостоятельного выполнения

1. Переведите на язык Бейсик алгоритмы решения задач 9-15 из § 11 и 1-7 из § 12. (Указание: в языке Бейсик действию ВЫЧИСЛИТЕЛЯ "Присвоить Z значение RND (А)" соответствует команда Z = 2*A*RND (1)-A.)

2. Найдите и исправьте ошибки в следующих программах.

а) Программа определения первого отрицательного члена последовательности а_n = sin (n/100) (n - натуральное число):

 10 IF BIN(N/100)<0 THEN 40 
 20 N = N + 1 
 30 GOTO 20 
 40 PRINT "ЗНАЧЕНИЯ N, SIN(N/100)" N, SIN(N/100)

б) Программы определения суммы первых десяти положительных членов последовательности a_n = cos (n), где n - натуральное число. В этих программах К обозначает количество найденных положительных членов последовательности, а S - сумму этих членов.

 10 К = 0 
 20 N = 1 
 30 WHILE К < = 10 
 40 IF C0S(N)>0 THEN 
    K = K + 1 : S = S + C0S(N) 
 50 N = N + 1 
 60 WEND

 10 К = 0 
 20 N = 1 
 30 IF K > 10 THEN 70 
 40 IF COB (N) > 0 
    THEN K = K + 1 : S = S + COS (N) 
 50 N = N + 1 
 60 GOTO 30

в) Программа нахождения значений In (n²- n) для целых п от - 5 до 5.

 10 FOR N = -5 TO 5 : IF N^2 - N< = 0 THEN 40 
 20 PRINT "ПРИ N = "N" ЗНАЧЕНИЕ ФУНКЦИИ НЕ ОПРЕДЕЛЕНО" 
 30 ELSE PRINT "ПРИ N = "N" ЗНАЧЕНИЕ ФУНКЦИИ РАВНО "LOG (N^2-N) 
 40 NEXT I

3. Многочлен х³ + 3х - 1 на отрезке [0; 1] имеет корень (почему?). Для его вычисления с точностью 0,1 была написана следующая программа:

 10 Х = 0 
 20 IF Х^3 + 3∗Х - 1> = 0 THEN 50 
 30 X = X + 0.1 
 40 GOTO 20 
 50 PRINT "КОРЕНЬ РАВЕН" Х

Злоумышленник поменял в ней две команды местами. Тем не менее ЭВМ и по испорченной программе все-таки нашла корень. Какие две команды переставил злоумышленник?

4°. Составьте программу нахождения корней уравнений с точностью 0,01 методом деления пополам, предварительно определив два числа, образующие "вилку":

5°. Составьте алгоритм нахождения знаменателя геометрической прогрессии, о которой известно, что сумма первых трех ее членов равна S₁, а сумма первых восьми ее членов равна S₂. Обеспечьте точность 0,01.

6°. Составьте математическую модель, алгоритм и программу для решения следующей задачи.

К одной точке на нитях одинаковой длины подвешены два шарика, одинаковых по массе и одинаково заряженных. Каков угол между нитями подвеса?

7°. Составьте математическую модель, алгоритм и программу для решения следующей задачи.

Два шарика соединены пружиной. Им сообщается одинаковый заряд. На сколько удлинится пружина?