§ 33. Системы счисления

Система счисления - способ записи чисел с помощью заданного набора специальных знаков (цифр). Еще в четвертом классе вы узнали, что привычная нам система счисления - позиционная и десятичная. Для записи любых чисел в ней используется десять всем хорошо известных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а значение каждой цифры (ее "вес") определяется той позицией, которую цифра занимает в записи числа. Так, запись 23 означает, что это число можно составить из 3 единиц и 2 десятков. Если мы поменяем позиции цифр, то получим совсем другое число - 32. Это число содержит 3 десятка и 2 единицы. "Вес" двойки уменьшился в десять раз, а "вес" тройки в десять раз возрос. Цифры десятичной записи числа - это просто коэффициенты его представления в виде суммы степеней числа 10-основания системы счисления:

(Запишите сами аналогичное представление для числа 341,89.) На самом деле числа можно записывать как сумму степеней не только числа 10, но и любого другого натурального числа, большего 1. Например, в Древнем Вавилоне использовалась система счисления с основанием 60. Делением часа на 60 минут, а минуты на 60 секунд мы обязаны именно этой системе счисления.

Тот факт, что основанием используемой нами системы счисления является число 10, объясняется, вероятно, тем, что природа наделила нас десятью пальцами на руках и десятью пальцами на ногах.

В вычислительных машинах обычно используется двоичная система счисления (ее основание - число 2). Для записи чисел в этой системе используются только две цифры - 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строились и строятся ЭВМ, могут находиться только в двух хорошо различимых устойчивых рабочих состояниях. По существу, эти элементы представляют собой обычные выключатели. Как известно, выключатель может быть либо включен, либо выключен. Третьего не дано. Отличие электронного выключателя от выключателя настольной лампы состоит в том, что в электронном выключателе нет механических движущихся частей и переключается он не рукой, а электрическим сигналом от другого выключателя. Время, переключения поэтому оказывается очень малым, порядка 10^-9 с. Одно из состояний выключателя обозначают цифрой 1, другое - цифрой 0.

Как же получить запись числа в двоичной системе счисления? Вы уже догадались: нужно представить число как сумму степеней двойки и выписать коэффициенты такого представления. При записи числа в различных системах счисления договоримся указывать основание используемой системы, например, справа внизу после самого числа:

(Приведите сами несколько примеров перехода от десятичной записи числа к двоичной и наоборот.)

Для представления информации вне ЭВМ применять двоичную систему с ее громоздкой записью неудобно. Здесь часто используются восьмеричная и шестнадцатеричная системы. В восьмеричной системе счисления числа записываются с помощью восьми цифр: 0, 1,2, 3, 4, 5, 6, 7. Сама восьмерка (как и основание любой системы счисления) записывается двумя цифрами: 10 (почему?). Для записи чисел в шестнадцатеричной системе необходимо располагать уже шестнадцатью различными символами, используемыми как цифры. В качестве первых десяти шестнадцатеричных цифр используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной системе они соответствуют числам 10, 11, 12, 13, 14, 15) используют буквы латинского алфавита - А, В, С, D, E, F.

Особая привязанность программистов к восьмеричной и шестнадцатеричной системам объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. При переводе в восьмеричную систему двоичное число из трех или менее цифр записывается одной цифрой:

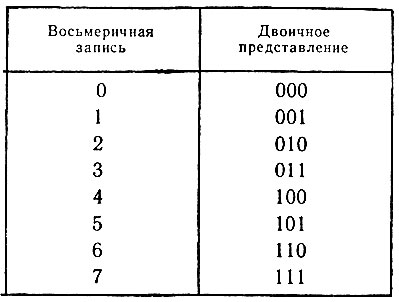
Пусть теперь нам нужно представить двоичное число, например 10101101011 112, в восьмеричной форме. Для этого двоичную запись числа разбивают на группы по три цифры справа налево, начиная с младшего разряда:

Затем каждую тройку цифр заменяют соответствующей цифрой восьмеричной системы счисления:

Еще несколько примеров:

Обратный переход - от восьмеричной системы к двоичной - осуществляется заменой каждой восьмеричной цифры соответствующей тройкой двоичных цифр. Переход от двоичной системы к шестнадцатеричной и обратно осуществляется аналогично. Только шестнадцатеричная цифра заменяется не на три, а на четыре двоичных цифры. Например:

Вопросы

1. Что такое система счисления?

2. Как переходить от записи числа в восьмеричной системе счисления к записи в двоичной и обратно?

3. Сколько цифр используется:

а) в двоичной системе;

б) в восьмеричной системе;

в) в десятичной системе;

г) в шестнадцатеричной системе;

д) в сташестидесятипятеричной системе?

Задания для самостоятельного выполнения

1. а) Переведите в десятичную систему двоичные числа 1000011110101, 1010010111011, 1110011001100110101.

б) Переведите в двоичную систему десятичные числа 123, 456, 1024, 4095.

в) Какое максимальное число можно записать в двоичной системе счисления двенадцатью цифрами?

2. а) Переведите в восьмеричную систему двоичные числа 11101110101001101001100110101, 110110110000110001011010101, 111011101010011.

б) Переведите в двоичную систему восьмеричные числа 54321, 545253, 777, 1010001.

3. а) Переведите в шестнадцатеричную систему двоичные числа 1110111010100110100110011, 110110110110001011010101, 111011100001010011.

б) Переведите в двоичную систему шестнадцатеричные числа 1АВ, A IB, E2E4, Е7Е5.