Случай - это...

В предисловии был задан вопрос "Что такое случай?", на который автор толком так и не ответил. Этому были две причины.

Во-первых, таков стиль научно-популярного изложения, от которого автор не собирается отказываться. Этот стиль требует задать с виду элементарный вопрос, напустить побольше туману и показать, что-де все не так просто, а совсем наоборот, то есть очень сложно и неэлементарно. После этого полагается солидно и с большим числом занятных, но доступных примеров открыть глаза изумленному читателю на его неосведомленность в этом вопросе и изложить современное состояние науки в выбранной области.

Другая причина была куда более важная. Дело в том, что у исследователей и ученых пока нет единого мнения о том, что называть случайностью. И поэтому автор, отвечая на поставленный вопрос, рискует вызвать в свой адрес нелестные замечания коллег. В этой истории занимает самую неудобную позицию - ему нужно высказать свое мнение. И поэтому, собрав все свое мужество, попробуем все же ответить на вопрос: что такое случайность?

Так вот, случайность - это прежде всего... непредсказуемость, которая является результатом нашего невежества, результатом нашего незнания, нашей слабой осведомленности, результатом отсутствия необходимой информации.

Такой случай является, по сути дела, мерой невежества! Чем меньше сведений мы имеем о предмете, тем случайнее для нас его поведение; и наоборот, чем больше мы знаем о предмете, тем менее случайно ведет себя и тем более определенно мы можем высказаться о его дальнейшем поведении.

С этой точки зрения К. А. Тимирязев совершенно прав. Ссылка на случайность какого-либо факта или процесса (в таком понимании) является подтверждением неосведомленности, некомпетентности исследователя в этом деле.

Построим модель такого случая. Будем причинно-следственную связь явлений выражать графически в виде круга и двух стрелок (рис. 1). Пусть стрелка, входящая слева в круг, символизирует причину явления, тогда стрелка, выходящая из круга справа, будет условным выражением следствия, вызванного этой причиной. Явление здесь представляется в виде преобразователя причины в следствие.

Рис. 1

Нам приходится на каждом шагу встречаться с подобными преобразователями. Нажимая кнопку на двери, мы создаем причину, которая вызывает следствие - звон колокольчика в квартире (рис. 2). Чтобы зажечь горелку газовой плиты, нужно возбудить две причины: поворотом краника пустить газ и поднести к горелке зажженную спичку. Эти две причины вызовут следствие - работу горелки (рис. 3).

Рис. 2

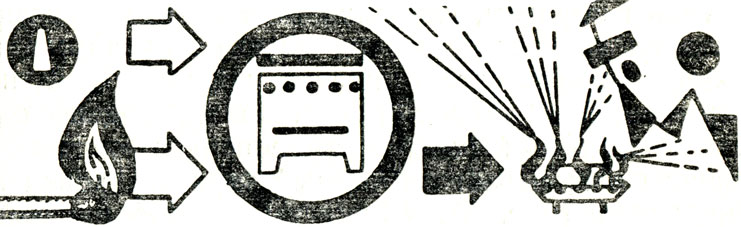
Рис. 3

Такое представление причинно-следственных связей очень удобно и широко распространено в кибернетике (рис. 4). Здесь сигнал А является причиной возникновения сигнала В. Связь между сигналами А и В осуществляется преобразователем, который выдает на выход сигнал В, как только на входе появится сигнал А, то есть

Рис. 4

Вернемся к примеру со звонком. Можно ли быть твердо уверенным, что при нажатии кнопки всегда зазвонит звонок? Конечно, нет! Прежде чем утверждать, что вас услышат, нужно знать, есть ли напряжение в цепи звонка.

Значит, чтобы зазвонил звонок, необходимы два условия: наличие напряжения в сети и нажатие кнопки. Только в этом случае звон колокольчика будет строго предопределен.

Но, подходя к двери, мы не знаем, есть ли напряжение в цепи звонка. Именно поэтому для нас звон колокольчика или его отсутствие является случайным событием. Эта случайность есть следствие нашей неосведомленности. Если бы предварительно мы спросили по телефону, работает ли звонок, то есть получили бы необходимую информацию, то для нас события "нажатие кнопки" и "звон звонка" уже были бы связаны строго необходимой связью и никакой случайности здесь не было.

Таким образом, случайность в данном примере возникла за счет того, что из двух необходимых причин звона колокольчика (нажатия кнопки А₁ и наличия напряжения в цепи А₂) обычно наблюдается только одна (нажатие кнопки), а неопределенность второй причины и вызывает случайный характер поведения колокольчика (рис. 5). (Здесь молчаливо предполагается, что звонок исправен, иначе был бы еще один источник случайности.)

Рис. 5

Аналогичная картина наблюдается при зажигании горелки газовой плиты (рис. 6). Кроме двух известных причин А₁ и А₂ (поворот краника и горение спички), необходимо знать состояние третьей причины - А₃ - наличия газа в сети (или баллоне). Если прежде чем зажечь газ, мы позвоним в управление газовой сетью и убедимся в ее исправности (или измерим давление в баллоне), то загорание горелки не будет случайным событием. Если же мы пренебрежем этой информацией, то должны смириться с тем, что горелка не всегда зажжется, и это событие станет случайным, то есть предсказуемым не на все 100 процентов.

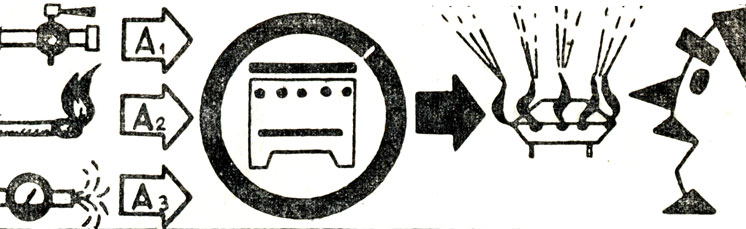
Рис. 6

Случайность, следовательно, по сути дела, зависит от уровня нашего незнания. Чем более невежествен человек, тем более для него случаен окружающий мир. И наоборот, ученому мир представляется не столь удручающе случайным.

Как видно, случайность - понятие субъективное, зависящее от запаса информации субъекта. Если бы бог существовал и если бы был действительно "всеведущим", то наш мир для него, по-видимому, не был бы случайным. Но, к сожалению, "вездесущими" способностями легенда наделила только бога. Даже его ближайшие архангелы при всей своей внеземной святости были обделены столь сильной способностью к получению необходимой информации. О грешных людях и говорить не приходится. Где им тягаться со сверхтелепатическими возможностями всевышнего! По пяти узким каналам сбора информации (зрение, слух, обоняние, осязание и вкус) человек получает скудную информацию об окружающем мире, и только за изворотливость ума его назвали "царем природы". Эта изворотливость и позволяет человеку объяснить механизм случайности примерно следующим образом.

Всякое событие (Б) является следствием малого или большого ряда причин. (См. стрелки А₁, А₂, А₃ ... на рис. 7, где точками символически обозначены другие стрелки - причины А₄, А₅, А₆..., которых может быть сколь угодно много.) Чтобы предсказать интересующее его событие, человеку необходимо точно узнать все причины, вызывающие появление этого события.

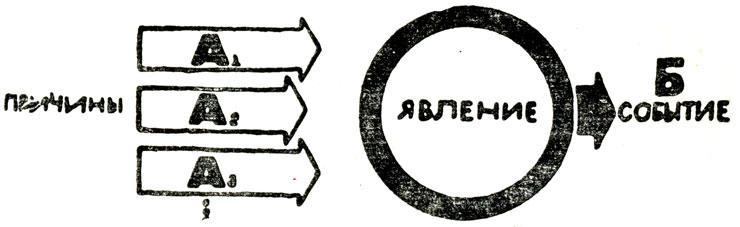
Рис. 7

В первом случае, когда этих причин немного и все их можно наблюдать, событие считается не случайным (его часто называют регулярным или детерминированным). Например, бросая камень, можно точно предсказать, что упадет на Землю, а не на Луну, Здесь знание закона тяготения или опыт, заменяющий это знание, несут исчерпывающую информацию о событии - месте падения камня.

Если же ряд причин слишком велик (например, если событие Б вызывается миллионом причин) и ввиду этого попросту не может быть охвачен одновременно, то интересующее нас событие уже нельзя предсказать точно, о станет случайным, непредсказуемым. Здесь случайность образуется за счет недостаточного знания, за счет некомпетентности, за счет слабой осведомленности.

Означает ли это, что в одно прекрасное время, когда мы станем уж очень умными, случайность исчезнет с нашей планеты?

Вовсе нет! Этому будут препятствовать по крайней мере три обстоятельства, которые надежно защищают случайность.

Прежде всего надо упомянуть бесконечную сложность мира.

Нам никогда не удастся исчерпать все многообразие мира и полностью познать его. Расчет на подобное божественное "всеведение" - более чем вера в бога. Это претензия на то, чтобы самому стать богом - вездесущим и всезнающим.

Проще говоря, существует известный запрет на исчерпание окружающего нас мира: сколько бы мы его ни исследовали, всегда останется "недочерпанное", ибо мир неисчерпаем. Афоризм Козьмы Пруткова "Нельзя объять необъятное" как нельзя лучше передает суть этого запрета.

Так, по-видимому, никогда не удастся определить, какой стороной ляжет на пол подбрасываемая монета, поскольку ее судьба определяется по крайней мере четырьмя факторами: человеком, который ее подбрасывает; средой, в которой монета летит; поверхностью, на которую а упадет, и особенностями самой монеты. Каждый из этих факторов играет существенную роль и, в свою очередь, определяется огромным числом причин. Причем количество этих причин практически бесконечно и, вероятно, не сможет быть охвачено одновременно при определении результата хотя бы одного эксперимента с монетой.

Далее, надежная зашита случайности и непредсказуемости нашего мира гарантируется ограниченной точностью измерений.

Известно, что точность предсказания какого-либо события часто зависит от точности измерения его причин (возмущающих факторов).

А точность всякого измерения ограниченна. С развитием науки и техники эта точность возрастает, но всегда остается (и будет оставаться) конечной, то есть никакие измерения нигде и никогда не станут абсолютно точными (хотя бы в силу атомного строения вещества). Это ограничивает возможности предсказания и приводит к появлению неопределенности, случайности.

Например, для определения точки попадания баллистической ракеты необходимо знать с огромной точностью состояние всех факторов, влияющих на ее траекторию. Это прежде всего состояние слоев атмосферы, через которую проходит ракета. Однако точное измерение движения масс воздуха в атмосфере, да еще в районе цели, представляет всегда огромные трудности и практически невозможно. Приходится ограничиваться приближенными оценками указанных факторов, что и определяет случайный, точно не предсказуемый характер попадания ракеты в цель.

И выходит, что невозможность наверняка поразить цель вызвана вовсе не слабостью управления, а является результатом отсутствия точной информации, которая в данном случае связана прежде всего с приближенностью измерений.

И последнее. Случайность является результатом не только нашего незнания, бесконечной сложности мира и ограниченной точности измерения причин, но и знаменитого соотношения неопределенностей.

Дело вот в чем. Все события, исход которых определяется взаимодействием отдельных атомов, случайны по своей природе. Это положение опирается на уже названный принцип (соотношение) неопределенности, который впервые сформулировал известный немецкий физик В. Гейзенберг. Смысл этого принципа сводится к следующему.

Как известно, для определения любого будущего состояния какой-либо частицы в пространстве достаточно точно узнать ее исходное положение и скорость. Принцип неопределенности заключается в том, что как бы накладывает ограничение на эту точность, если объектом исследования является микрочастица. А именно: точность определения одного из указанных параметров микрочастицы (например, положения) зависит от точности определения другого параметра - скорости, вернее - импульса. Это означает, что чем точнее будет определен один параметр, тем больше неточность в определении другого параметра; оба же параметра с необходимой высокой точностью одновременно определить нельзя. В этом состоит природа микромира. И никакое развитие техники измерения не позволит увеличить эту точность, так же как никакое развитие науки никогда не позволит нам активно вмешиваться в прошлое. (Заметим, что интерпретировать прошлое можно и мы часто пользуемся этим, однако изменить его нам не удастся.)

Действие принципа неопределенности хорошо иллюстрирует следующий простой опыт. Возьмем обычную телевизионную трубку - кинескоп. Внутри этой трубки имеется источник электронов - так называемая электронная пушка. Говоря проще, это обычная раскаленная спираль, какую мы видим в электролампочке, горящей вполнакала. Эта спираль и является источником электронов. Их можно ускорить в электрическом поле, а затем, пропуская через два следующих друг за другом маленьких отверстия в стволе пушки, получить тот самый пучок электронов, которым а "стреляет". Электроны, вылетающие из ствола "пушки" двигаются узким пучком в направлении к экрану, покрытому специальным слоем, чувствительным к ударам электронов.

Попадая на экран, разогнанный электрон дает видимую глазом вспышку-точку, а пучок электронов - светящееся пятно. Управляя движением электронного пучка (это легко осуществляется электрическим или магнитным полем), можно изменять положение пятна на экране, что и лежит в основе телевидения.

Однако сейчас нас интересует не это. Зададимся целью сделать пятно на экране кинескопа как можно меньше. Для этого следует утоньшать электронный пучок, вылетающий из жерла электронной пушки. Как добиться такого? Кажется, нет ничего проще: достаточно уменьшать жерло пушки. Представим, что нам удалось создать пушку с изменяющимся отверстием от большого до самого малого - диаметром в электрон (меньше делать не надо, так как электрон попросту "застрянет" в стволе). Вероятно, это будет нечто вроде диафрагмы фотоаппарата. "Диафрагмируя" электронную пушку, мы сможем воздействовать на толщину электронного пучка.

Теперь начнем эксперимент. Уменьшая диафрагму, первое время мы действительно будем уменьшать размер пятна на экране трубки. Но затем оно перестанет уменьшаться, и вокруг него образуются слабо светящиеся кольца, которые по мере дальнейшего уменьшения диафрагмы станут расширяться. А при самом маленьком диаметре жерла пушки, равном диаметру электрона, пятно исчезнет вовсе и по всему экрану равномерно будут вспыхивать то там, то здесь точки, фиксирующие положения отдельных электронов.

Как объяснить такое поведение частиц-электронов? Ведь на первый взгляд кажется, что при самом узком отверстии пучок должен стать самым тонким и все электроны должны были бить в одну и ту же точку экрана, и, следовательно, световое пятно должно быть равным диаметру электрона. В эксперименте же ничего подобного не наблюдалось. В чем дело?

А дело в том, что предполагаемый результат эксперимента противоречит изложенному выше принципу неопределенности. Действительно, по мере сужения отверстия ошибка в определении положения пролетающих электронов становилась все меньше и меньше (эта ошибка равна разности диаметров отверстия и электрона, и а по мере уменьшения диаметра отверстия стремится к нулю). При совпадении этих диаметров положение электрона определяется точно: в момент пролета отверстия находится внутри отверстия, и его координаты в точности совпадают с положением центра отверстия. В соответствии с принципом неопределенности такая точность в определении положения должна лечь тяжелым грузом на возможность определения дальнейшей судьбы электрона, то есть на его последующее движение (скорость). Это и наблюдалось в эксперименте, когда электрон можно было встретить с равной вероятностью в любой точке экрана. Напомним, что скорость определяется не только величиной, но и направлением, которое в данном случае становилось неопределенным, то есть случайным.

Следовательно, фиксируя положение электрона, мы никак не можем (не в состоянии и никогда не будем в состоянии) определить направление его дальнейшего движения, то есть его скорость, с точностью большей, чем позволяет это принцип неопределенности Гейзенберга.

Случайность здесь имеет принципиальный характер, и она не снимается никакими мерами по повышению точности измерения.

Таков наш мир, таковы его объективные закономерности! Надежда, что в будущем удастся избавиться от этой случайности, бесперспективна и беспочвенна.

Таким образом, микрооснова нашего мира случайна, и опирается а на соотношение неопределенностей.

Из этого следует весьма важный и поучительный вывод об уникальности каждого конкретного эксперимента, вывод о строгой неповторимости результатов, который идет вразрез с классической наукой.

Действительно, старая добропорядочная наука прошлого века утверждала, что совершенно необходимо, чтобы в одних и тех же условиях всегда получались бы одни и те же результаты. Именно этого и не получается! Если даже и удается вполне точно вторично воспроизвести все условия эксперимента, то и в этом гипотетическом случае мы получим иной результат. Что же это? Крах науки? Нет! Это новый шаг в познании. Вероятностный характер нашего мира в принципе накладывает запрет на точное предсказание. Всякая экстраполяция (предсказание) будущего имеет всегда принципиально случайный характер. "Тем не менее, - по остроумному замечанию известного американского физика Р. Файнемана, - несмотря на это, наука жива".

Как же жить в таком мире, где ничего нельзя точно предвидеть? Оказывается, ничего страшного в этом нет.

Во-первых, предел точности, допускаемый принципом неопределенности, очень мал (порядка размеров атомного ядра). И сказывается этот принцип лишь в измерениях на атомном уровне. А во-вторых, от наличия непредсказуемости наш мир не становится менее уютным.

В самом деле, эту непредсказуемость можно рассматривать как помеху, мешающую точным измерениям. Но современная наука выработала мощные средства борьбы с погрешностями в измерении (о них мы будем говорить позже) и позволяет снимать (точнее, делать безболезненными) неприятности, связанные с непредсказуемостью.

Но вернемся к макромиру.

В микромире мы, грубо говоря, никогда не сможем точно предсказать будущее положение микрочастицы. Но всякое макровзаимодействие, то есть взаимодействие крупных тел, складывается из большого числа микровзаимодействий, результат которых в соответствии с принципом неопределенности точно предсказать нельзя. Следовательно, будущее поведение тел мы можем определить не точно, а лишь приближенно, с некоторой неабсолютной достоверностью.

Проиллюстрируем сказанное на простом примере. Рассмотрим опыт с обычной игральной рулеткой, которая представляет собой мелкую тарелку с сотней лунок на дне. В эту тарелку с определенной скоростью выпускается маленький легкий шарик, который, многократно ударяясь о края тарелки, постепенно теряет свою скорость и попадает в одну из лунок, определяя тем самым выигрыш. Пусть шарик и рулетка выполнены идеально гладко, гладко даже на атомном уровне (предположим на минутку, что это удалось сделать). Представим также, что шарик выпускается некоторым гипотетическим идеально точным механизмом из одного и того же положения в строго определенном направлении со строго одинаковой скоростью. Означает ли это, что в конечном счете будет попадать в одну и ту же лунку?

Нет, не означает! После каждого соприкосновения со стенкой рулетки шарик ввиду рассмотренного принципа неопределенности будет отскакивать в направлении, которое можно предугадать лишь вероятностным образом. Каждую же конкретную траекторию предугадать будет нельзя, ибо она определяется на атомном уровне (здесь имеются в виду атомы стенки и шарика в точке их соприкосновения). А так как скорость шарика по условию нам известна с достаточной точностью, то его конечное положение будет несколько неопределенно.

Очевидно, что с каждым отскоком неопределенность в положении шарика возрастает (она как бы складывается) и к моменту его остановки становится максимальной. Это обстоятельство и делает игральную рулетку принципиально случайной машиной, результат работы которой можно предугадывать лишь приближенно. И никакие новые, самые точные методы измерения не помогут нам предугадать положение шарика в момент остановки более точно, чем это допускает принцип неопределенности.

Заметим еще раз, что речь шла об идеальной рулетке, которая, несмотря на свою "идеальность", все же является случайной машиной. Реальная же рулетка имеет значительно большую непредсказуемость, вытекающую из естественной шероховатости и неоднородности поверхности реального шарика и корытца рулетки. Значит, неопределенность реальной рулетки складывается из неопределенности, вызванной принципом Гейзенберга, и неопределенности, порожденной шероховатостью соприкасающихся поверхностей. При этом доля второй неопределенности значительно превышает первую, то есть реальная рулетка - это случайная машина, где основной источник случайности находится не на атомном уровне, а получен за счет неидеальности соприкасающихся поверхностей, за счет плохой обработки этих поверхностей. Однако и поведение "идеальной" рулетки также непредсказуемо.

Любопытно, что хозяин рулетки всегда заинтересован в ее максимальной непредсказуемости. В самом деле, если бы в рулетке наблюдалось предпочтение каких-либо лунок и шарик попадал бы в них чаще, чем в другие, то игроки, заметив это, начали бы делать ставки именно на эти лунки и разорили бы хозяина. И чтобы этого избежать, стремится свою рулетку делать максимально случайной машиной с максимальной непредсказуемостью результата.

По упомянутым причинам окружающий нас мир является миром случайным, вероятностным. Его случайный характер образуется как за счет свойств самого мира, так и из-за ограниченных возможностей людей, для которых часто не очень важно, где именно сидит случайность - в существе ли явления или появляется в результате взаимодействия человека с окружающим его миром.

Резюмируя, можно сказать, что случайность нашего мира держится на следующих трех китах:

1) на принципе неопределенности;

2) на неисчерпаемости вселенной;

3) на ограниченности человеческих возможностей (на данный момент времени, разумеется).

Взаимодействие этих трех факторов и формирует неопределенность в нашем трижды случайном мире.

Как же действовать в такой обстановке?

Прежде всего следует расстаться с иллюзией, что от случайности можно избавиться насовсем. Для этого придется придумать новый мир, отличный от того, в котором мы живем.

Такой мир, например, придумал когда-то ученый Лаплас. Он говорил, что все явления в мире строго предопределены предыдущим его состоянием. Вот его слова, в которых формулируется эта точка зрения.

"Мы должны рассматривать настоящее состояние вселенной как следствие ее предыдущего состояния.

Ум, которому были известны для какого-либо данного момента времени все силы, одушевляющие природу, и относительное положение всех ее составных частей, если бы вдобавок оказался достаточно обширным, чтобы подчинить эти данные анализу, обнял бы в одной формуле движения величайших тел вселенной наравне с движениями легчайших атомов; не осталось бы ничего, что было бы для него недостоверно: и будущее, так же как и прошедшее, предстало бы перед его взором".

Как видно, мир Лапласа не что иное, как фильм, записанный на бесконечной ленте, который так же бесконечно развертывается перед нами. Мы являемся участниками этого фильма и действуем в строгом соответствии со сценарием, написанным бог знает кем.

Несостоятельность подобного мира очевидна. Это не наш мир!

Кроме простой обидности - действительно, очень обидно быть марионеткой в чьих-либо руках, - Лапласова вселенная вызывает более серьезные возражения.

Мир Лапласа предопределен, а следовательно, фаталистичен. Будет так, как написано в сценарии, и все тут! Как ни бейся - ничего нового не добьешься. А то, что ты бьешься, - это тоже записано в сценарии!

Таков мир по Лапласу.

А как же быть с нашей трижды случайной вселенной? Как поступать в той или иной случайной ситуации, которую нельзя предвидеть? Можно ли разумно действовать в случайной обстановке? Как "утилизировать" случайность?

На все эти вопросы попробуем ответить в следующих разделах книги, посвященных несчастному и счастливому случаям. В первом разделе рассмотрены меры борьбы со случайностью; во втором обсуждаются способы использования случая во благо человека.