На вход приемника поступает сообщение, посланное в виде посылок А и В. Помехи их сильно исказили. Как приемник распознает, когда послано А, а когда В?

Теперь заглянем на "кухню" создания идеального приемника Простые и наглядные рассуждения В. Котельникова хорошо раскры вают интересующий нас механизм взаимодействия сигнала и помехи в приемнике.

Пусть передается уже известный нам простейший но универсальный двоичный сигнал. Он, естественно, может быть лишь одним из двух дискретных значений: А или В.

Так как систем связи без помех принципиально не существует, тр и на входе нашего приемника действует некая помеха. Она есть напряжение того эквивалентною генератора помех, о котором мы говорили раньше. Будем считать, что генератор создает наиболее "зловредную" и наиболее "вездесущую" помеху в виде непрерывного, хаотически меняющегося напряжения или силы тока ("белый, шум").

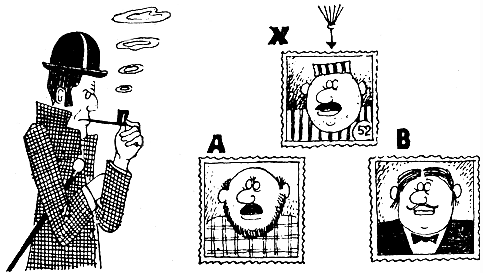
Сигнал и помеха, складываясь на входе приемника, образуют суммарное напряжение X. Для приемника это действительно некий таинственный "икс", так как неизвестно, произошел ли он от сложения помехи с сигналом А или с сигналом В. Вот эту альтернативу и должен решить, да еще наилучшим из возможных способом, приемник.

Но как он ее решит, если, во-первых, на приеме неизвестно, какой из двух сигналов пошлет в данный отрезок времени передатчик (если это известно, то тогда нечего и передавать, никакая информация не передается). А во-вторых, как мы уже говорили, принципиально неизвестно, какой выброс в это время даст помеха: большой или маленький, взлет или падение, острый или плавный...

Можно ли узнать, из чего "сделан" наш конкретный "ИКС"поступивший в данный отрезок времени на вход приемника? Нет, и еще раз нет! А как же быть?

Очень просто: игнорировать конкретные значения сигнала и помехи в конкретные моменты времени и рассматривать и сигнал и помеху как два независимых случайных процесса, каждый из которых подчинен своим закономерностям.

И тут мы должны просить его величество Случай помочь нам. Ведь он владеет целой империей, именуемой "теория вероятностей", где есть такие области, как "случайные события", "случайные процессы", "теория игр", "теория операций" и т. д.

Сначала скажем, что приемник при поступлении на его вход этого таинственного X регистрирует на выходе при одних его значениях сигнал А, а при других - сигнал В.

Следовательно, по окончании сеанса связи приемник запишет, скажем, на ленте длинную последовательность знаков А и В, часть из которых будет истинной (совпадающая с переданными), а часть ложной (под действием помех А превратилась в В или В в А).

Принципиально невозможно указать, где на этой ленте ложь, а где правда. Но Случай подсказывает, что, используя специальную теорему, называемую теоремой Бейса, можно подсчитать, какое будет среднее число ошибок во всей принятой последовательности. А это не так уж мало. По этим данным можно сравнивать между собой и приемники, и методы передачи и принимать решение, верить ленте или не верить.

Расчет по Бейсу тоже, конечно, требует некоторых знаний о сигнале и помехе, но уже не конкретных, а "в среднем": как часто передается А и как часто В, а также как часто помеха принимает то или иное значение.

Первое определяется характером передаваемого текста: в большинстве случаев А и В идут одинаково часто и вероятность их появления равна 0,5. Второе зависит от характера помех и определяется так называемой "плотностью вероятности распределения ее амплитуд". В. Котельников взял наиболее характерный случай: помехи типа тепловых шумов (белый шум), распределенные по так называемому нормальному закону.

Опуская подстановку этих закономерностей в формулу Бейса, выведенную еще до появления радиотехники, сразу приведем результат, полученный В. Котельниковым. Вот, как он выглядит: 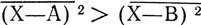. Приведенная запись означает следующее: из поступившего на вход таинственного X в приемнике надо образовать две разности путем вычитания из него сигнала А и сигнала В. (Значит, на приеме должны быть точно известны два возможных образца сигнала.) Эти разности возводятся в квадрат и усредняются. Потом проводится последняя операция - разности сравниваются по величине. Если левая скобка, где фигурирует А, больше правой, то идеальный приемник регистрирует на выходе сигнал В (этот случай записан в нашем неравенстве). Если имеет место обратное неравенство, то приемник выдает сигнал А.

Читатель, наверное, уже догадался, почему именно так должно быть. Ведь если X и В очень похожи друг на друга, а X и А не очень похожи, то скорей всего X образовался из В путем добавления к нему небольшой помехи. В этом случае правая часть неравенства будет меньше и приемник зарегистрирует сигнал В.

Правда, могло случиться, что X образовался в данном случае и из А путем добавления большой помехи. Тогда даже идеальный приемник сделает ошибку. А так как чем больше помеха, тем меньше ее вероятность, то эти ошибки будут редким явлением. Такую же закономерность мы наблюдаем на бушующем море: гигантские волны, гребни которых вздымаются на многие метры, редки, средних значительно больше, а небольших волн очень много.

Вычисляя разности (X-А) и (X-В), мы, по существу, устанавливаем похожесть (корреляцию) принятого сигнала на один из двух истинных. Пусть у нас в приемнике хранятся "портреты" сигналов А и В и из антенны в приемник поступил некий сигнал X. Если мы установим, на кого он больше похож - на А или на В, то тем самым решим нашу задачу.

Метод сличения портретов, впервые открытый В. Котельниковым, оказался лучшим из возможных способов приема сигналов, пораженных помехами. Он получил название корреляционного, или оптимального, метода приема и в настоящее время широко используется.

Этот метод реализует все, что может предоставить нам случай. Лучшего пути для раскрытия нашего таинственного "икса", объединившего в себе и случайность сигнала, и случайность помехи, нет и не может быть. Это строго показано В. Котельниковым.