В. Котельников показал, что из-за помех даже идеальный приемник дает ошибки. К. Шеннон же установил, что определенное число битов в секунду можно передать без единой ошибки даже при действии помех. Как примирить эти два вывода?

В. Котельников поставил и решал задачу: какое число битов информации будет "в среднем" обязательно искажено помехами даже при приеме на идеальный приемник. К. Шеннон позже нашел решение более общей задачи: какое число битов можно передать без единой ошибки по каналу связи за одну секунду, невзирая на наличие помех. Но ведь даже идеальный приемник дает ошибки. Как же примирить эти два подхода?

Для ответа на этот вопрос вначале обратимся к принятой К. Шенноном универсальной модели систем связи, ставшей классической. До этого любую систему связи рассматривали в отрыве от "источника информации" и "адресата". К. Шеннон смело ввел их в модель и показал, что полноценное изучение систем связи без них невозможно.

Источником информации и адресатом могут быть, естественно, и живые существа (люди, дельфины, пчелы, бабочки) и различные автоматы (реле, самописец, телеграфный аппарат, магнитофон).

Источник информации вырабатывает сообщение, которое поступает на передатчик. Последний выполняет весьма ответственную роль: преобразовывает сообщение в сигнал, посылаемый на прием, и усиливает его. Это преобразование может быть и очень простым, и очень сложным. Например, вы подходите к дверям гостиницы. и они сами распахиваются перед вами. Ваше тело, нарушив прохождение инфракрасного луча, тем самым подало сигнал на автомат, открывающий дверь. Следовательно, сообщение о вашем приближении преобразовано в прерывание луча.

Идет разговор по телефону. Передатчиком является микрофон, на выходе которого напряжение меняется пропорционально силе голоса говорящего. (Я, как и многие другие, часто забываю, что разговор "во весь голос" для лучшей слышимости нарушает эту пропорциональность и приводит к обратному эффекту.)

Миссию, выполняемую передатчиком, называют кодированием. Выше мы разбирали методы погрузки информации на бегунов-носителей. Это частные случаи кодирования. Еще не зная этого термина, мы уже им занимались. Вспомните, как для противодействия помехам мы пять раз повторяли команды, посылаемые на зенитную ракету. Это есть один из методов кодирования.

Из передатчика сигнал поступает в среду распространения, общую для передатчика и приемника. Здесь и находится беговая дорожка наших бегунов, бережно несущих заданную информацию.

В некоторых искусственных средах они мчатся как по рельсам: по проводам, по кабелям, по волноводам и световодам. Такие рельсы иногда создает природа: например, паук, придя в гости к соседке, передает информацию о своем прибытии, закодировав ее в виде серии импульсов и передавая их путем подергивания одной из периферийных паутинок тенеты. Здесь механические колебания распространяются по паутинкам-рельсам.

Другой вид беговых дорожек - это свободное пространство. Если передатчик излучает радиоволны во все стороны, то бегуны тоже несутся во все стороны; они заполняют все окружающее пространство и, конечно, быстро "выдыхаются". Такие всенаправленные сигналы излучают, в частности, аварийные передатчики пароходов, самолетов, парашютистов.

Если нацелить всех наших бегунов точно в направлении на корреспондента (если его положение известно), то передача информации будет значительно экономичнее. Эту задачу решают антенны, входящие в состав передатчика. Так, чтобы сигнал-марафонец добежал до финиша у планеты Венера, когда там находился наш корабль "Венера-8", потребовалась антенна гигантских размеров, создающая очень узкую беговую дорожку в пространстве.

Но не только радиоволны распространяются в свободном пространстве, хотя и там разрешены не все пути-дорожки. Звуковые волны в воде хорошо переносят информацию между подводными лодками. Для них тоже стараются по возможности сузить беговую дорожку, чтобы увеличить дальность и, главное, не обнаруживать себя.

В среде распространения и происходят самые большие неприятности с передачей информации. Дикая орда чертей-помех набрасывается на сигналы и старается превратить их в хаос, лишенный информации. Если бы не они, то все было бы. просто. Не нужно было бы специальной науки, которую называют "Теория информации" или "Теория передачи сигналов". Не нужно было бы студентам учить лишний курс. Не надо было бы писать эту книжку...

Но, как мы установили, они в "грубом", реальном мире неизбежны. И, каким бы ни был могущественным на выходе передатчика сигнал, всегда найдется участок пути, где биты и черти оказываются приблизительно в одинаковой весовой категории и где начинаются кровавые баталии меж ними.

Да и сама среда часто ведет себя коварно. Она меняет степень затухания сигнала, отчего он то царит над шумами, то падает ниже их. Кроме того, среда влияет на изменение времени прохождения сигнала от передатчика к приемнику. Это особенно опасно в фазовом приемнике, так как нарушает шкалу времени и тем самым фазу сигнала (надеюсь, читатель еще не забыл это!).

Наконец, самый коварный трюк, выкидываемый средой, состоит в том, что иногда вместо одного посланного сигнала в приемник приходит несколько, и со сдвигами во времени. Эти запаздывающие копии сигнала накладываются на следующий посланный сигнал и т. д. Образуется невероятная каша из сигналов, да еще приправленная гарниром из помех. Многие десятилетия казалось, что разобраться в этой каше невозможно. Однако человеческий гений преодолел и это.

Пройдя через ту или иную среду, смесь сигнала и помех поступает на вход приемника. Здесь на подмогу внешним чертям спешат внутренние, засевшие в приемнике. Как мы уже знаем, их можно объединить с внешними и вынести из приемника. Это и сделано на нашей схеме. Так как обычно сигнал довольно слаб, то его усиливают в приемнике, а затем производят операцию, обратную кодированию: декодируют, то есть преобразуют электрический сигнал в исходное сообщение.

Выше мы разбирали некоторые способы снятия информации с наших бегунов. Способы эти и являются частными случаями декодирования. Так, в результате декодирования входных сигналов телеграфный аппарат печатает текст, а телевизионный приемник воспроизводит изображение.

Наконец, принятое сообщение поступает к адресату, к потребителю информации. На этом и заканчивается путешествие сигнала по шенноновской универсальной схеме канала связи.

Легко видеть, что в нее можно вписать самые различные системы. Например, локатор следит за движущимся самолетом. Источником информации будет здесь, конечно, не наземный передатчик, облучающий самолет периодически следующими импульсами, а сам самолет: меняя положение, он будет то раньше, то позже отражать импульсы. Но самолет не только источник формации, но и передатчик ее. Он как бы переизлучает импульсы, посланные с земли. А приемник сравнивает посланные и отраженные импульсы и по величине запаздывания определяет расстояние до самолета. Оператор или автомат, получив эти данные, принимает решение.

Аналогичным образом в схему можно вписать дельфина с его биологическим -локатором, определяющим расстояние до стайки рыб, до собратьев и т. д. Теперь вернемся к вопросу, поставленному в начале новеллы. Мы видели, что даже идеальный приемник не может гарантировать правильный прием всех посланных битов. Некая часть их неизбежно искажается. К. Шеннон показал, как, невзирая на искажение некоторых битов, можно обеспечить неискаженную передачу всей информации, переносимой ими. Иначе говоря, он показал, что даже из ненадежных элементов связи можно создать нечто вполне надежное. Каким образом? Да путем соответствующего кодирования сообщений.

Идея, грубо говоря, сводится к следующему. Если иметь в виду дискретные сигналы, то надо отказаться от переноса информации одиночной посылкой и заменить ее группой посылок, построенной так, что искажение одной или нескольких посылок в этой группе не исказит сообщения, передаваемого всей группой.

Подробнее мы это разберем дальше, а сейчас важно другое. Методов кодирования можно придумать очень много. Уже сейчас их столько, что даже специалистам трудно их все помнить, К. Шеннон перешагнул через все конкретные методы кодирования и поставил перед собой такую задачу: определить, какое предельное количество неискаженных битов можно передать по системе связи при самом совершенном методе кодирования.

Это предельное число он назвал емкостью, или пропускной способностью, системы связи и обозначил буквой С. Как нельзя в ведро емкостью в 10 литров влить воды больше, чем 10 литров, так нельзя по системе связи передать в одну секунду большее число неискаженных битов, чем С, при любом методе кодирования.

Оказалось, что С зависит только от двух величин: от полосы пропускания системы связи F и от отношения мощности сигнала Рс к мощности шума Рш на входе приемника. А сама знаменитая формула К. Шеннона, заслуженно называемого отцом теории информации, выглядит так:

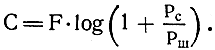
Из формулы сразу видна коварная зависимость емкости С от мощности сигнала: увеличив мощность передатчика, скажем, в 1000 раз, мы повысим емкость его всего в три раза. И все это делает логарифм. Вот, наверное, почему я его с детства не любил. Он не позволяет нам "перекричать" помехи.

Непрерывное нарастание темпа жизни требует непрерывного повышения скорости передачи информации и ее достоверности. Поэтому сопоставление реально передаваемого числа битов с предельными возможностями вскрывает те резервы, которые человек еще не исчерпал. А резервы эти огромны. Расчеты показывают, что достигнутые скорости в десятки и сотни раз ниже предельных.

А можно ли практически полностью реализовать величину С? Методика вывода формулы К. Шеннона показывает, что для приближения к этому пределу надо применять все более и более сложные методы кодирования. И все больше и больше увеличивать длительность кодирующих последовательностей, или тех групп, о которых мы говорили. А это требует все большей памяти в приемном устройстве и приводит к все возрастающему запаздыванию в приеме сообщения. В пределе, при передаче со скоростью, равной пропускной способности канала связи С, это запаздывание беспредельно возрастает.

Ситуация перекликается с известным анекдотом. Вы получаете телеграмму "Сидоров выиграл автомобиль Волгу ждите коррекций". На следующий день приходит коррекция: "Не Сидоров, а Иванов ждите коррекций". Еще через день: "Не Волгу а швейную машину ждите коррекций". На третий день: "Не выиграл а проиграл ждите коррекций"...

Но это не значит, что нельзя, совершенствуя методы кодирования, заметно приблизиться к пределу и тем самым увеличить скорость передачи в реальных системах связи в десятки и сотни раз.