В бюраканских дискуссиях фигурировала одна формула, которую почти все участники писали мелом на доске или ссылались на нее. Кому принадлежит эта популярная формула?

Время от времени участники дискуссии для большей убедительности приводили те или иные формулы. Но была одна формула, которую почти все участники писали на доске мелом или ссылались а нее. На вид она очень проста: некая величина N равна простому роизведению семи коэффициентов. Эта "некая величина" есть не то иное, как самая сверхсекретная величина для землян, в том исле и для участников симпозиума, - число внеземных цивилизаций в нашей Галактике, способное по своему уровню развития науки и техники вступить с нами в контакт! Раз есть формула, да еще такая простая, значит, можно вычислить N и тут же узнать, сколько у нас братьев по разуму? Можно было бы! Но эти семь коэффициентов как раз и образуют тот гордиев узел, который землянам предстоит развязать или разрубить. Обратимся к самой формуле.

Вот она:

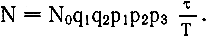
Сомножители, вокруг которых и шли горячие споры, имеют следующие значения:

N_o - число звезд с очень длительным устойчивым состоянием, необходимым для зарождения и эволюции жизни от простейших форм до разумных и далее.

q₁ - доля звезд, удовлетворяющих первому условию, но обязательно имеющих планетные системы.

q₂ - доля звезд, удовлетворяющих первому и второму условию, но планеты которых находятся в "зоне жизни" (на них не слишком жарко, но и не слишком холодно, и жизнь возможна).

p₁ - вероятность зарождения жизни на планетах, находящихся в зоне жизни.

p₂ - вероятность того, что зародившаяся жизнь успешно эволюционирует в разумную.

р₃ - вероятность того, что развитие разума идет по технологическому пути (создание и непрерывное совершенствование орудия труда), а не по пути приспособления к окружающей среде (путь, начатый у нас дельфинами).

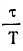
отношение времени существования цивилизаций от периода достижения высокого технологического уровня (например, от освоения радиосвязи) до своей гибели, к полному времени существования биологического вида (от его зарождения до гибели). Эта формула была выведена несколько лет назад участником симпозиума Ф. Дрейком и известна как "формула Дрейка". Для ее полного освоения давайте сделаем сообща расчет по ней. При этом, задаваясь теми или иными значениями сомножителей, мы, по существу, будем моделировать некую вселенную, которая им удовлетворяет и, возможно, очень непохожа на ту, в которой мы с вами, читатель, фактически обитаем. Вот куда завлекла нас эта простая с виду формула.

Будем считать, что, например, из 100 звезд нашей Галактики только на одной из них длительное время существуют стабильные температурные, радиационные и другие условия, необходимые для зарождения и развития жизни хотя бы на одной из ее планет (на Земле. этот процесс занял три миллиарда лет с гаком). Общее число звезд в Галактике равно 10 11. Следовательно, первый коэффициент равен

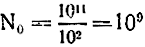
Далее будем считать, что, допустим, половина из этих звезд совершает свой путь в просторах холодного космоса не в скучном одиночестве, а со свитою планет (минисвита - одна планета). Прямых методов наблюдения планет у звезд; исключая, естественно, Солнце, пока нет. Они слишком бледны на фоне пылающих звезд. Однако различными косвенными методами установлено, что звезды с планетной свитой весьма распространенное явление. В частности, профессор Стенфордского университета Боб Оливер рассказал на симпозиуме об изучении пульсаций в движении "летящей звезды Бернарда" (она совсем "рядом" - 6 световых лет от Земли). Анализ пульсаций показал, что вокруг этой звезды вращаются, как минимум, три планеты с массами всего лишь в 200, 300 и 400 раз большими, чем масса нашей планеты. Итак, полагаем

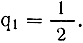
Планеты, очень близкие к своей звезде и очень далекие от светила, находятся вне "зоны жизни" (если жизнь вне Земли мыслить в какой-то мере похожей на нашу). Если обозначить эту зону для солнечной системы, то в нее попадают Венера, Земля и Марс. В отношении Земли сомнений в существовании жизни и даже разумной (во всяком случае, по нашим земным критериям, которые другим цивилизациям могут показаться очень "частными и узковедомственными") как будто нет. Великую же тайну Марса и Венеры скоро нам раскроют автоматы или космонавты, которые уже нацеливают туда свои траектории.

Пусть из каждых четырех звезд с длительным устойчивым режимом и имеющих планеты окажется одна счастливая, у которой есть планета в зоне жизни. Тогда коэффициент

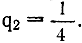
Переходим, к тайне зарождения жизни. Здесь земная наука пока только разводит руками или сваливает все на этот "случайный, случайный, случайный мир". В "густом соленом бульоне", который заполнял впадины нашей планеты в глубокой древности, случайно образовалась (и возможно, только одна-единственная) сложная Молекула, способная к размножению, к повторению себя. Вот она и заварила кашу, которую мы теперь гордо называем земной цивилизацией.

Как-то в докладе я имел неосторожность сказать приблизительно то же, и меня стал буквально преследовать один из слушавших. Он никак не мог согласиться с тем, что все живое на нашей планете: и разум, и наша пышная цивилизация, и, наконец, он сам - есть чисто случайное явление (по простому и ясному определению, случайное явление - это явление, которое может либо произойти, либо нет). В конце концов его удалось несколько успокоить тем, что, невзирая на случайность зарождения жизни на Земле или на конкретной планете любой другой звезды, общее число возникающих цивилизаций в Галактике подчиняется определенным, пока нам неизвестным закономерностям.

Вместе с тем профессор Ф. Крик подверг резкой критике идею чисто случайного зарождения жизни. Если подсчитать вероятность возникновения сложной молекулы, способной размножаться от простого "перетряхивания" молекул в бульоне, то она оказывается невероятно малой, сверхуникальной. И это ставит всю проблему CETI под великое сомнение. Ф. Крик считает, что, возможно, при определенных физических условиях возникают какие-то силы, которые способствуют образованию больших и сложных молекулярных структур типа белков.

В связи с этим чрезвычайно важно для всей проблемы установить, есть ли жизнь в любой форме на других планетах нашей звезды.

Возвращаясь к нашему коэффициенту, примем "среднепотолочное" его значение p₁ = 1/10. То есть из десяти звезд с планетами, находящимися в зоне жизни, только у одной происходит это таинственное явление - зарождение жизни.

Какие шансы у зародившейся жизни достичь в процессе длиннющей, отнюдь не прямолинейной эволюции, разумного рубежа, рубежа самопознания материи? Примем для нашего примера этот шанс также равным одному из десяти, то есть р₂ - 1/10.

Возможен ли нетехнологический путь развития цивилизации? Мне кажется это невероятным. Ведь только труд, создание и совершенствование орудий труда формирует сознание. Но имеется и другая точка зрения. Поэтому примем коэффициент р₃ - 0,8 (из десяти только две цивилизации приходят к разуму, не намозолив рук или щупалец).

Наконец, последний коэффициент. Не останавливаясь здесь на возможных путях развития цивилизации (гибель ее в результате, например, атомной войны; потеря интepeca к технике и отказ от технологического пути развития; физическое и духовное вырождение и т. д.), примем для нашего примера время существования вида равным одному миллиарду лет, а время технологической эры равным одному миллиону лет. Следовательно,

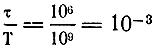
Теперь, подставляя все величины в формулу Дрейка, получаем:

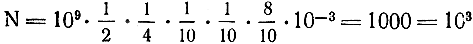
Таким образом, из наших расчетов следует, что при сделанных допущениях в нашем Млечном Пути число созревших для контакта с нами цивилизаций составляет одну тысячу, то есть в среднем каждые сто миллионов звезд имеют только одну цивилизацию!

Но мы просто упражнялись, чтобы выявить пружины этого таинственного числа N. А что говорят ученые? Расчеты по формуле Дрейка и другими методами делали ученые разных стран, в том числе и трое из участников симпозиума: К. Саган, И. Шкловский, фон Хорнер. Наибольший оптимизм в выборе исходных данных проявил К. Биле, его результат N_Б = 10¹⁰. Это значит, что в среднем на десять звезд приходится одна "цивилизованная". На полюсе пессимизма оказался фон Хорнер. По его расчетам, N_x = 10⁴. Или одна "цивилизованная" звезда приходится только на десять миллионов звезд!! (Число, близкое к полученному нами в примере.) Тут невольно вспоминаешь несколько вольное определение, кто такой пессимист: оказывается, это есть не что иное, как хорошо проинформированный оптимист. Тем не менее различие приведенных оценок на шесть порядков, или в миллион раз, говорит о слишком больном "коэффициенте незнания" данного вопроса. Но нам сейчас даже не так важно знать, сколько их, а есть они или их нет. Если нет, то и нечего копья ломать: искать их, пытаться наладить контакт, приглашать их в гости или напрашиваться к ним. А на этот фундаментальный вопрос мы получаем из всех расчетов, даже при самых пессимистических допущениях, положительный ответ: да, они есть! Мы не одиноки! Мы не уникальны!

Это мнение, этот оптимистический взгляд на жизнь и разум вселенной красной нитью проходил во всех бюраканских дискуссиях, и он нашел отражение в решении, о котором речь впереди.