Почти все основные показатели нашей цивилизации растут по так называемому экспоненциальному закону. Что это за закон?

Для разговора о будущем нам необходимо, хотя бы кратко, познакомиться с основными тенденциями в развитии нашей земной цивилизации. Для этого стоит познакомиться с так называемым экспоненциальным законом, по которому сейчас растут почти все основные показатели нашего сообщества; познакомиться тем более, что этой экспонентой то и дело пугают землян западные футурологи.

Темп развития земной цивилизации, и, наверное, не только земной, можно в целом оценивать по темпу роста таких основных показателей, как потребляемые энергия и вещество, народонаселение, количество научной и технической информации и т. д.

Анализ роста этих показателей за ряд последних столетий убеждает, что он происходит очень быстро, по так называемой экспоненте. Й этот закон, эта экспонента стали неким жупелом. "...Как услышу я слово жупел, так руки-ноги затрясутся", - писал А. Н. Островский).

Давайте обследуем этот закон.

Выглянуло весеннее солнце. Снег подтаивает. Вы слепили снежок, пустили его вниз по крутому склону и наблюдаете, как он катится. Снежок облипает снегом и быстро растет, как на дрожжах: чем больше его масса, тем больше на него налипает снега, и тем быстрее он разрастается. В этом и есть вся премудрость экспоненты, ее грозный закон. Но откуда это замысловатое слово?

Оно введено в математику более двухсот лет назад Леонардом Эйлером. Сам закон получается вот откуда. Обозначим нарастающую массу нашего снежного кома через у; тогда скорость ее нарастания есть производная массы по времени, то есть

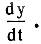
Если обходиться без высшей математики, то можно эту же скорость вычислить, деля прирост массы кома Δy на время Δt, за которое он произошел,

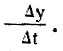
Экспоненциальная зависимость требует прямой пропорциональности в каждый момент между растущей массой кома у и скоростью налипания на ком снега

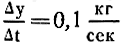
точнее,

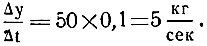
Пусть начальный снежок, который вы слепили, имел массу, равную 1 килограмму (у = 1); пустив его по склону, вы предоставили возможность ему набрать скорость. Через секунду у него возникла скорость налипания в

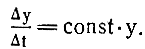
(сто граммов в секунду). В средней части склона его масса возросла в 50 раз (у = 50 кг). Если есть прямая пропорциональность между у и

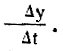
то скорость налипания снега на ком тоже должна возрасти в 50 раз и стать

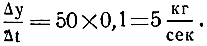
следовательно, общее условие прямой пропорциональности запишется так

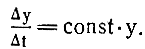
Если такая зависимость справедлива, например, для народонаселения планеты, то с увеличением его, скажем, в три раза скорость его прироста тоже должна возрасти в три раза. Это, в свою очередь, ускорит дальнейшее нарастание численности населения и, соответственно, такое же нарастание скорости его прироста и т. д.

Если ничто не нарушит прогресса с такой прямой пропорциональностью, то у может достичь сколь угодно больших величин.

В примере со снежным комом естественным ограничением явится длина снежного склона.

Если склон очень длинен, например, вы бросили свой снежок с вершины Эльбруса, то при больших значениях у сильно возрастет сопротивление воздуха, это замедлит его движение, скорость налипания

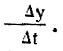
- упадет, нарастание кома замедлится, прямая пропорциональность нарушится.

Теперь естественно спросить: по какому же закону должна нарастать во времени масса нашего снежного кома у, чтобы была прямая пропорциональность между у и

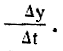
Оказывается, есть только одна удивительная функция, которая при всех значениях пропорциональна своей производной (и своему интегралу), удовлетворяющая нашему уравнению. Вот она y = y₀ · e^at,

где у_о - начальная масса нашего кома (снежок) в момент t = 0, а α - постоянный коэффициент, зависящий в нашем примере от крутизны склона и состояния снега.

Графическое изображение этой зависимости называется экспонентой. А нарастание какой-либо величины по такому закону получило название экспоненциального.

Кривая эта спокойно занимала свое скромное место в гигантском арсенале математических функций и не подозревала, что ей уготована такая великая честь - определять развитие основных показателей земной цивилизации (в том числе и самой математики).

Теперь эта роль вскрыта, и ее загадочное имя - экспонента - замелькало в книгах, журналах, докладах.

Количество вырабатываемой на земном шаре энергии растет по экспоненте. Так как вся энергия в конечном счете переходит в тепловую, то это может привести к изменению климата планеты. В самом деле, Земля ежесекундно поглощает, а следовательно, и излучает обратно около 5 · 10²³ эрг солнечной радиации. Для того чтобы климат Земли заметно не изменился, надо ограничить вырабатываемую энергию приблизительно одним процентом от этой величины. Можно принять, что современная энергетика вырабатывает 4 · 10¹⁹ эрг в секунду. Подсчитаем и увидим, как скоро начнем портить природный климат.

Мировая статистика показывает, что период удвоения количества вырабатываемой на Земле энергии составляет всего 25 лет. Подставив эти данные в уравнение экспоненты, находим, что через время t = 125 годам энергетика землян достигнет этого рубежа в 1 процент от получаемой от Солнца энергии. Значит, если, как говорят математики, экспонента будет продолжать все эти 125 лет работать, то нашим внукам и правнукам грозит изменение климата Земли, к которому человек так привык и приспособился за последние сотни тысяч лет.

Где выход? Можно предложить "заморозить" нашу энергетику на уровне одного процента или вблизи него. Но это значило бы "заморозить" и цивилизацию. А цивилизация, как мы уже говорили, или может успешно развиваться, или "катиться дальше вниз". Среднего устойчивого состояния у этой сложнейшей системы нет! Тем более что народонаселение планеты также растет по экспоненте, и жизнеобеспечение требует обязательного роста энергетики.

Но ведь нас окружают необъятные просторы космоса. Для вселенной, как это ни парадоксально звучит, характерны не сгустки материи в виде звезд и их скоплений, а бескрайние просторы, космические пустыни, почти лишенные материи. Значит, можно энергодобывающие и энергопоглощающие предприятия размещать в окружающем космосе и не калечить колыбель человечества - дорогую старушку Землю.

Весь "ужас" экспоненты проявляется в полную меру, если продолжить наши расчеты дальше, на дальнейшее существование человечества.

Так, сохраняя тот же период удвоения в 25 лет, что составляет 4 процента годового прироста, в течение 240 лет добыча энергии должна превзойти всю энергию, посылаемую Солнцем Земле; через 800 лет превысит всю энергию, излучаемую Солнцем; а через 1500 лет - даже превзойти излучение Галактики!

Аналогичные парадоксальные цифры можно получить и для других показателей, определяющих развитие нашей цивилизации.

Теперь нам ясны корни "экспоненциального жупела". Они проистекают от формального распространения законов истекшего периода на ближайшее и более далекое будущее.

Но ниоткуда не следует, что, во-первых, эти законы именно такими должны быть и дальше (ведь "система" умная, с регулированием и обратной связью) и, во-вторых, что не будут найдены принципиально новые решения (как, например, с энергетическими трудностями).