Мера определенности - энтропия

Наибольшая степень неопределенности соответствует тому случаю, когда все исходы опыта или ожидаемого события одинаково вероятны, - например, 50 шансов за выздоровление и 50 против. Прогноз "70 шансов за и 30 против" уже определеннее, а ответ врача "99 за и один против" предсказывает ход событий почти с полной уверенностью.

Как видим, степень неопределенности зависит от распределения вероятностей. Она максимальна, если все исходы события представляются одинаково вероятными. Наоборот, при резко неравномерном распределении вероятностей (одни исходы весьма вероятны, другие почти совсем невероятны) степень неопределенности мала: мы почти наверняка знаем, что именно произойдет. Как показал Шеннон, количественно степень неопределенности Н может быть выражена довольно простой математической формулой

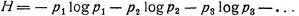
В этой формуле р₁ означает вероятность первого исхода, р₂- вероятность второго исхода и т. д., а все логарифмы берутся при основании 2. Если вероятность выздоровления 50% (пятьдесят шансов из ста) - неопределенность Н=1; если же вероятность выздоровления 95%-неопределенность Н = 0,33, то есть в три раза меньше.

Введенная Шенноном мера неопределенности Н получила название энтропия¹.

¹ (Слово "энтропия" употреблялось в физике и раньше. Оно обозначало степень неопределенности микроскопического состояния системы, макроскопическое состояние которой задано (температура и давление газа в сосуде полностью характеризует его макроскопическое состояние, однако микроскопические детали этого состояния - расположение, скорость и направление движения каждой молекулы в отдельности - остаются еще в значительной степени неопределенными).)

Теперь мы можем сказать, что количество информации в статистическом сообщении q_ст равно количеству информации в категорическом сообщении q_кат минус степень неопределенности (энтропия) Н, остающаяся после получения статистического сообщения:

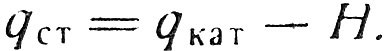
Очень часто случается, что еще до получения сообщения мы можем заранее оценить вероятности его вариантов. Например, ожидая известие о результатах шахматного турнира, мы уже знаем шансы его участников. В этом случае окончательное сообщение должно только ликвидировать ту неопределенность, ту неполную уверенность в исходе турнира, которая у нас имелась. Чем больше была неопределенность, тем больше информации принесло ликвидировавшее ее сообщение.

Это соображение является весьма общим. Количество информации в сообщении лучше всего измерять энтропией-степенью той неопределенности, которую оно "снимает". Можно показать математически, что все предыдущие определения получаются из данного как его частные случаи. Вот почему понятия "энтропия" и "количество информации" так тесно связаны между собой.