Переадресация команд

Сущность "переадресации" может быть пояснена на примере вычисления значений площади круга для некоторых заранее указанных (или ранее вычисленных) значений его радиуса, разделенных неодинаковыми интервалами.

В 20-ю ячейку памяти (рис. 27) помещаем число π, в 21-ю, 22-ю, 23-ю и следующие ячейки (например, до 80-й) - различные значения радиуса, для которых должны вычисляться площади. 19-я ячейка будет использоваться для помещения в нее промежуточных результатов, а в ячейках № 81 и 82 хранятся специальные числа, необходимые для переадресации (значение их выяснится в дальнейшем). Вычисления производятся по следующей программе:

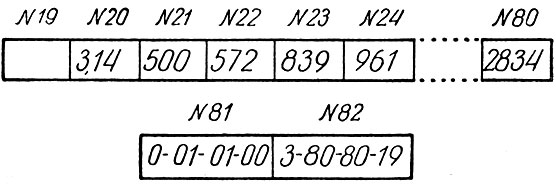
Рис. 27. Исходные данные в запоминающем устройстве

По первой команде вычисляется квадрат первого значения, радиуса (из ячейки № 21), который затем по второй команде умножается на тс. По третьей команде вычисленное значение площади круга заносится в таблицу окончательных результатов.

Теперь нужно повторить те же самые операции, но уже над новым значением радиуса, хранящимся не в 21-й, а в 22-й ячейке. Для этого можно было бы включить в программу в качестве четвертой команды "3-22-22-19" (возвести новое значение радиуса в квадрат) с последующим повторением второй и третьей команд без изменения. Затем должна следовать команда "3-23-23-19" (возвести в квадрат значение радиуса из ячейки № 23) и т. д. При большом количестве различных значений радиуса программа получалась бы громоздкой.

Легко сообразить, что вводимые вновь команды 3-22--22-19, 3-23-23-19 и т. д. могут быть получены из первой команды 3-21-21-19 путем последовательного прибавления к ней числа 0-01-01-00, хранящегося в ячейке № 81:

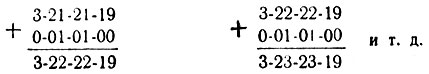
Таким образом, посредством арифметических действий над числом, изображающим команду, может быть осуществлено систематическое изменение ее адресов (в данном случае первого и второго), а если потребуется, то и кода действия.

Такая операция, называемая "переадресацией", как раз и осуществляется по четвертой команде рассматриваемой программы. При этом число, изображающее новую ("переадресованную") команду, направляется в ту же ячейку № 1, где хранилась исходная команда (в случае надобности переадресованную команду можно было бы поместить и в другую ячейку памяти).

По пятой команде выполняется сравнение переадресованной команды (числа) из ячейки № 1 с командой 3-80-80-19, специально введенной для этого в ячейку № 82. Пока первый и второй адреса переадресованной команды не больше 80 (использованы еще не все значения радиуса, хранящегося в ячейках № 21 ÷ 80) согласно команде сравнения осуществляется возврат к началу программы - исполнению переадресованной первой команды. Когда же все значения радиуса будут исчерпаны, команда примет вид 3-81-81-19, то есть превзойдет число в ячейке № 82, и по команде сравнения машина перейдет к выполнению следующей (шестой) команды, означающей остановку.

Как было уже сказано, переадресация команд наряду с периодическим их повторением и другими приемами, разрабатываемыми в теории программирования, неизмеримо расширяет возможности счетной машины и позволяет решать на ней сложнейшие задачи высшей математики, хотя арифметическое устройство машины "умеет" выполнять только четыре простейших арифметических действия. Возможность многократного повторения этих действий в сложнейших комбинациях, меняющихся в зависимости от ранее полученных результатов, с успехом заменяет другие, более, сложные средства математического анализа и открывает перед быстродействующей электронной машиной широчайшие перспективы практического использования. Быстрота выполнения операций позволяет решать многие задачи даже простейшим методом планомерных и притом очень многочисленных проб, то есть фактически методом подбора. Таким образом, ограниченность математических средств машины в большинстве случаев искупается быстротой и гибкостью ее работы.