4.8. Правила де Моргана
В задачах, решаемых с помощью алгебры логики, часто используются два правила, известных под названием правил де Моргана. Приведем формулировку этих правил:
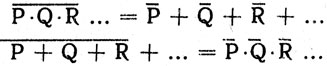
Многоточия, использованные в приведенных формулах, означают, что в выражении может содержаться произвольное число переменных. Вот несколько примеров использования данных правил:
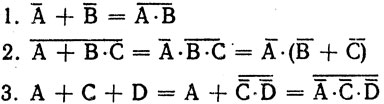
Первый пример достаточно прост. Во втором примере сначала выражение 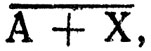 где X = В*С, преобразуется к виду
где X = В*С, преобразуется к виду 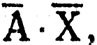 а затем
а затем 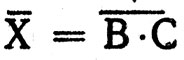 приводится к виду
приводится к виду 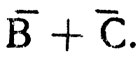 В третьем примере с помощью первого правила из С + D получаем
В третьем примере с помощью первого правила из С + D получаем 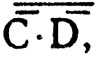 а затем выводим окончательный ответ.
а затем выводим окончательный ответ.
Применение правил де Моргана обычно сводится к последовательному выполнению следующих трех шагов:
а) отрицание всех отдельных термов выражения;
б) замена операций AND на OR и наоборот;
в) отрицание всего выражения.
На практике правила де Моргана используются для представления произвольных логических функций в виде, удобном для реализации их с помощью электронных логических элементов одного типа.
В частности, все функции из табл. 4.8 можно представить с помощью суперпозиции функций И-НЕ (NAND) или ИЛИ-НЕ (NOR). Например, функция h = p*q (AND) может быть выражена с помощью NAND в виде 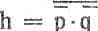 или с помощью NOR в виде
или с помощью NOR в виде 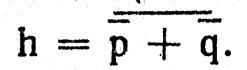 Функция отрицания реализуется в данном случае с помощью свойства поглощения, например, следующим образом:
Функция отрицания реализуется в данном случае с помощью свойства поглощения, например, следующим образом: 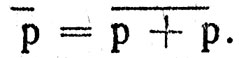 Эти преобразования применяются на практике при проектировании аппаратуры вычислительных устройств, что позволяет рационально использовать элементную базу. В заключение добавим, что любые логические функции могут быть представлены также с помощью функций IMPLIES и NOT.
Эти преобразования применяются на практике при проектировании аппаратуры вычислительных устройств, что позволяет рационально использовать элементную базу. В заключение добавим, что любые логические функции могут быть представлены также с помощью функций IMPLIES и NOT.
Упражнение 4.6
Запишите следующие выражения в двух вариантах с помощью NAND (а) и NOR (б):
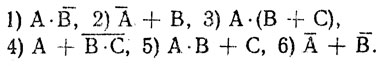
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'