3. Код Фано - экономный код
Алфавита из двух (а подавно - из большего числа) символов, как мы убедились в § 1, достаточно для кодирования любого множества сообщений. Устанавливая этот факт, мы кодировали все сообщения словами одинаковой длины, что, однако, далеко не всегда бывает выгодно.
Представим себе, что одни сообщения приходится передавать довольно часто, другие - редко, третьи - совсем в исключительных случаях. Понятно, что первые лучше закодировать тогда короткими словами, оставив более длинные слова для кодирования сообщений, появляющихся реже. В результате кодовый текст станет в среднем короче, и на его передачу потребуется меньше времени.
Впервые эта простая идея была реализована упоминавшимся нами американским инженером Морзе в предложенном им коде. Рассказывают, что создавая свой код, Морзе отправился в ближайшую типографию и подсчитал число литер в наборных кассах. Буквам и знакам, для которых литер в этих кассах было припасено больше, он сопоставил более короткие кодовые обозначения (ведь эти буквы встречаются чаще). Так, например, в русском варианте азбуки Морзе буква "е" передается одной точкой, а редко встречающаяся буква "ц" - набором из четырех символов.
В математике мерой частоты появления того или иного события является его вероятность. Вероятность события А обозначают обычно символом Р(А) или просто буквой Р. Не останавливаясь на определении вероятности, заметим только, что вероятность некоторого события (сообщения) можно представлять себе как долю тех случаев, в которых оно появляется, от общего числа появившихся событий (сообщение).
Так, если заданы четыре сообщения А1, А2, А3, А4 с вероятностями P(A1) = 1/2, Р(А2) = 1/4, Р(А3) = Р(А4) = 1/8, то это означает, что среди, например, 1000 переданных сообщений около 500 раз появляется сообщение А1, около 250 - сообщение А2 и примерно по 125 раз - каждое из сообщений А3 и А4.
Эти сообщения нетрудно закодировать двоичными словами длины 2, например так, как показано в следующей таблице:
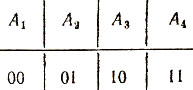
Таблица 7
Однако при таком кодировании вероятность появления сообщений никак не учитывается. Поступим теперь иначе. Разобьем сообщения на две равновероятные группы: в первую попадает сообщение А1, во вторую - сообщения A2, А3, А4. Сопоставим первой группе символ 0, второй - символ 1 (см. таблицу 8; во второй графе таблицы указаны вероятности сообщений).
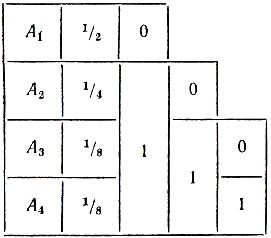
Таблица 8
Это вполне в духе принципа, применявшегося в задаче с угадыванием. Действительно, символ 0 соответствует ответу "да" на вопрос "принадлежит ли сообщение первой группе?", а 1 - ответу "нет". Разница лишь в том, что раньше все множество разбивалось на две группы с одинаковым числом элементов, теперь же в первой группе один, а во второй - три элемента. Но, как и раньше, разбиение это таково, что оба ответа "да" и "нет" равновозможны. Продолжая в том же духе, разобьем множество сообщений А2, А3, A4 снова на две равновероятные группы. Первой, состоящей из одного сообщения А2, сопоставим символ 0, а второй, в которую входят сообщения А3 и А4, - символ 1. Наконец оставшуюся группу из двух сообщений разобьем на две группы, содержащие соответственно сообщения А3 и A4, сопоставив первой из них 0, а второй - символ 1. Сообщение А1 образовало "самостоятельную" группу на первом шаге, ему был сопоставлен символ 0, слово 0 и будем считать кодом этого сообщения. Сообщение А2 образовало самостоятельную группу за два шага, на первом шаге ему сопоставлялся символ 1, на втором - 0; поэтому будем кодировать сообщение А2 словом 10. Аналогично, для А3 и А4 выбираем соответственно коды 110 и 111. В итоге получается следующая кодовая таблица:
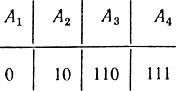
Таблица 9
Указанный здесь способ кодирования был предложен американским математиком Фано. Оценим тот выигрыш, который дает в нашем случае код Фано по сравнению с равномерным кодом, когда все сообщения кодируются словами длины 2. Представим себе, что нужно передать в общей сложности 1000 сообщений. При использовании равномерного кода на их передачу потребуется 2000 двоичных символов.
Пусть теперь используется код Фано. Вспомним, что из 1000 сообщений примерно 500 раз появляется сообщение Ль которое кодируется всего одним символом (на это уйдет 500 символов), 250 раз - сообщение А2, кодируемое двумя символами (еще 500 символов), примерно по 125 раз - сообщения А3 и А4 с кодами длины 3 (еще 3 × 125 + 3 × 125 = 750 символов). Всего придется передать примерно 1750 символов. В итоге мы экономим восьмую часть того времени, которое требуется для передачи сообщений равномерным кодом. В других случаях экономия от применения кода Фано может оказаться еще значительнее.
Уже этот пример показывает, что показателем экономности или эффективности неравномерного кода являются не длины отдельных кодовых слов, а "средняя" их длина l‾, определяемая равенством:
l‾ = ∑Ni=1 li P(Ai),
где li - длина кодового обозначения для сообщения Ai, P(Ai) - вероятность сообщения Ai, N - общее число сообщений.
Наиболее экономным оказывается код с наименьшей средней длиной l‾. В примере для кода Фано
l‾ = 1 × 0,5+2 × 0,25 + 3 × 2 × 0,125 = 1,75,
в то время как для равномерного кода средняя длина l‾ = 2 (она совпадает с общей длиной кодовых слов).
Нетрудно описать общую схему метода Фано. Располагаем N сообщений в порядке убывания их вероятностей: P(A1) ≥ P(A2) ≥ ... ≥ P(AN). Далее разбиваем множество сообщений на две группы так, чтобы суммарные вероятности сообщений каждой из групп были как можно более близки друг к другу. Сообщениям из одной группы в качестве первого символа кодового слова приписывается символ 0, сообщениям из другой - символ 1. По тому же принципу каждая из полученных групп снова разбивается на две части, и это разбиение определяет значение второго символа кодового слова. Процедура продолжается до тех пор, пока все множество не будет разбито на отдельные сообщения. В результате каждому из сообщений будет сопоставлено кодовое слово из нулей и единиц.
Понятно, что чем более вероятно сообщение, тем быстрее оно образует "самостоятельную" группу и тем более коротким словом оно будет закодировано. Это обстоятельство обеспечивает высокую экономность кода Фано.
Описанный метод кодирования можно применять и в случае произвольного алфавита из d символов с той лишь разницей, что на каждом шаге следует производить разбиение на d равновероятных групп.
Алгоритм кодирования Фано имеет очень простую графическую иллюстрацию в виде множества точек (вершин) на плоскости, соединенных отрезками (ребрами) по определенному правилу (такие фигуры в математике называют графами). Граф для кода Фано строится следующим образом (см. рис. 3). Из нижней (корневой) вершины графа исходят два ребра, одно из которых помечено символом 0, другое -символом 1. Эти два ребра соответствуют разбиению множества сообщений на две равновероятные группы, одной из которых сопоставляется символ 0, а другой - символ 1. Ребра, исходящие из вершин следующего "этажа", соответствуют разбиению получившихся групп снова на равновероятные подгруппы и т. д. Построение графа заканчивается, когда множество сообщений будет разбито на одноэлементные подмножества. Каждая концевая вершина графа, т. е. вершина, из которой уже не исходят ребра, соответствует некоторому кодовому слову. Чтобы указать это слово, надо пройти путь от корневой вершины до соответствующей концевой, выписывая в порядке следования по этому пути символы проходимых ребер. Например, вершине а3 на рис. 3 соответствует слово 100, а вершине а6 - слово 1110 (вершины, соответствующие кодовым словам, помечены на рисунке кружками).
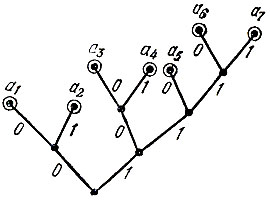
Рис. 3
Граф для рассмотренного выше примера представлен на рис. 4.
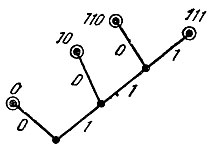
Рис. 4
Получающиеся для кодов Фано графы всегда обладают тем свойством, что они не содержат замкнутых контуров. Такие графы называют деревьями (мы будем называть их, учитывая происхождение, кодовыми деревьями). Кодовые деревья можно строить не только для кодов Фано, но и для других кодов. Независимо от алгоритма кодирования каждому дереву соответствует определенное множество кодовых слов. Например, для кодового дерева, изображенного на рис. 3, имеем:
a1 = 00, а2 = 01, а3 = 100, а4 = 101, а5 = 110, а6 = 1110, а7 = 1111.
Кодовое дерево может быть построено для кода с произвольным основанием d. Каждое его ребро помечается тогда одним из d символов алфавита и из каждой вершины такого дерева исходит самое большее d различных ребер. Например, на рис. 5 представлено кодовое дерево для троичного кода со следующим множеством кодовых слов: 0, 10, 11, 120, 121, 20, 21, 220, 221, 222. Кодовые деревья дают удобное геометрическое представление для многих важных понятий и облегчают, как мы увидим, решение различных задач, возникающих при построении экономных кодов.
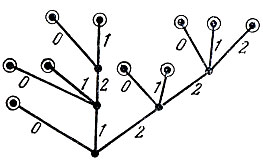
Рис. 5
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'