6. Оптимальный код

Как уже говорилось, общее правило при построении экономного кода следующее: чаще встречающиеся сообщения нужно кодировать более короткими кодовыми словами, а более длинные слова использовать для кодирования редких сообщений. Это правило и было реализовано в рассмотренном выше методе кодирования Фано. Но всегда ли метод Фано приводит к наиболее экономному коду? Оказывается, нет. Способ построения оптимального кода, который мы здесь изложим, потребует от нас более тонких рассуждений.

Пусть сообщения A₁, А₂, ..., A_N имеют вероятности р₁, р₂, ..., p_N (р₁ ≥ р₂ ≥ ... ≥ p_N) и кодируются двоичными словами a₁, a₂, ..., a_N, имеющими длины l₁, l₂, ..., l_N. Постараемся выяснить, какими свойствами должен обладать двоичный код, если он оптимален.

1. В оптимальном коде менее вероятное сообщение не может кодироваться более коротким словом, т. е. если p_i < р_j, то l_i ≥ l_j.

Действительно, в противном случае поменяем ролями I кодовые обозначения для A_i и А_j. При этом средняя длина кодовых слов изменится на величину

т. е. уменьшится, что противоречит определению оптимального кода.

2. Если код оптимален, то всегда можно так перенумеровать сообщения и соответствующие им кодовые слова, что

р₁ ≥ р₂ ≥ ... ≥ p_N и при этом

l₁ ≤ l₂ ≤ ... ≤ l_N. (1)

В самом деле, если р_i > р_i+1, то из свойства 1 следует, что l_i ≤ l_i+1. Если же p_i = p_i+1, но l_i > l_i+1, то переставим сообщения А_i и A_i+1 и соответствующие им кодовые слова. Повторяя эту процедуру нужное число раз, мы и получим требуемую нумерацию.

Из неравенств (1) следует, что сообщение A_N кодируется ловом a_N наибольшей длины l_N.

3. В оптимальном двоичном коде всегда найдется, по крайней мере, два слева наибольшей длины, равной l_N, и таких, что они отличаются друг от друга лишь в последнем символе.

Действительно, если бы это было не так, то можно было бы просто откинуть последний символ кодового слова a_N, не нарушая свойства префиксности кода. При этом мы, очевидно, уменьшили бы среднюю длину кодового слова.

Пусть слово a_t имеет ту же длину, что и a_N и отличается от него лишь в последнем знаке. Согласно свойствам 1 и 2 можно считать, что l_t = l_t+1 = ... = l_N. Если t ≠ N-1, то можно поменять ролями кодовые обозначения a_t и a_N-1, не нарушая при этом неравенств (1).

Итак, всегда существует такой оптимальный код, в котором кодовые обозначения двух (наименее вероятных) сообщений A_N-1 и A_N отличаются лишь в последнем символе.

Отмеченное обстоятельство позволяет для решения задачи рассматривать только такие двоичные коды, у которых кодовые обозначения a_N-1 и a_N для двух наименее вероятных сообщений A_N-1 и A_N имеют наибольшую длину, отличаясь лишь в последнем символе. Это значит, что концевые вершины a_N-1 и a_N кодового дерева искомого кода должны быть соединены с одной и той же вершиной а предыдущего "этажа" (см. рис. 12).

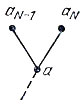
Рис. 12

Рассмотрим новое множество сообщений A⁽¹⁾ = {A₁, А₂, ..., A_N-2, А} с вероятностями p₁, p₂, ..., p_N-2, p = p_N-1 + p_N. Оно получается из множества {A₁, А₂, ..., A_N-2, A_N-1, A_N} объединением двух наименее вероятных сообщений A_N-1, A_N в одно сообщение A. Будем говорить, что A⁽¹⁾ получается сжатием из {А₁, А₂, ..., A_N-2, A_N-1, A_N}.

Пусть для A⁽¹⁾ построена некоторая система кодовых обозначений K⁽¹⁾ = {a₁, a₂, ..., a_N-2, a}, иными словами, указано некоторое кодовое дерево с концевыми вершинами a₁, a₂, ..., a_N-2, a. Этой системе можно сопоставить код К = {a₁, a₂, ..., a_N-2, a_N-1, a} для исходного множества сообщений, в котором слова a_N-1 и a_N получаются из слова а добавлением соответственно 0 и 1. Процедуру перехода от К⁽¹⁾ к К назовем расщеплением.

Справедливо следующее утверждение, открывающее путь для построения оптимального кода:

Если код К⁽¹⁾ для множества сообщений A⁽¹⁾ является оптимальным, то оптимален также и код К для исходного множества сообщений.

Для доказательства установим связь между средними длинами l‾ и l'‾ слов кодов K и K⁽¹⁾. Она, очевидно, такова:

Предположим, что код K не является оптимальным, т. е. существует код К₁ со средней длиной l₁‾ < l‾. Как отмечалось, можно считать, что концевые вершины a˜_N-1 и a˜_N его кодового дерева (см. рис. 13) соответствуют кодовым обозначениям для наименее вероятных сообщений A_N-1 и A_N. Тогда эти обозначения отличаются лишь в последнем символе. Рассмотрим код K⁽¹⁾₁ = {a˜₁, ..., a˜_N-2, а˜}, в котором слово а˜ получается из a˜_N-1 отбрасыванием последнего символа. Средние длины l‾₁ и l'‾₁ связаны соотношением, аналогичным (2):

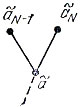
Рис. 13

Из неравенства l₁‾ < l‾ следует l'‾₁ < l'‾, что противоречит оптимальности кода K⁽¹⁾. Утверждение доказано.

Теперь ясно, что для построения оптимального кода южно использовать последовательные сжатия исходного множества сообщений.

Проиллюстрируем процесс последовательных сжатий и расщеплений на примере множества из пяти сообщений с вероятностями p₁ = 0,4; р₂ = р₃ = р₄ = р₅ = 0,15. Процесс этот отражен в следующей таблице:

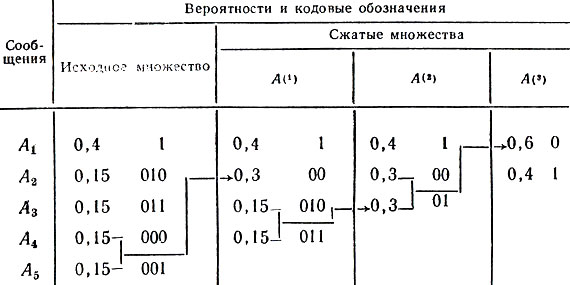
Таблица 12

Каждое из множеств А⁽¹⁾, А⁽²⁾, А⁽³⁾ получается сжатием предыдущего множества. Множество А⁽³⁾ состоит из двух сообщений, поэтому оптимальный код K⁽³⁾ содержит два кодовых обозначения - 0 и 1. Последовательное расщепление K⁽³⁾ дает оптимальный код для исходной системы сообщений.

Средняя длина l‾ кодовых слов, равная 0,4 + 4 × 3 × 0,15 = 2,2, является, как это следует из предыдущего, минимально возможной для данного множества сообщений.

Описанный метод кодирования был предложен в 1952 г. американским математиком Д. А. Хаффменом и называется его именем. Сравним теперь оптимальный код из таблицы 12 с кодом Фано для того же множества сообщений, который строится ниже.

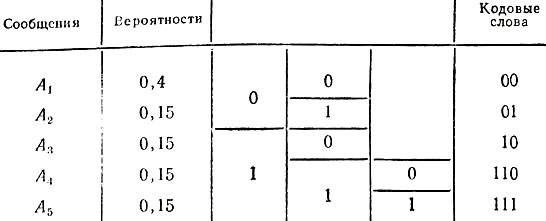
Таблица 13

Подсчитаем среднюю длину l‾_F кодовых слов в этом случае:

Следовательно, метод кодирования Фано не всегда приводит к оптимальному коду.

Как и метод Фано, метод кодирования Хаффмена может быть распространен на случай кодового алфавита, состоящего из произвольного числа символов. Этот вопрос рассмотрен в книге [2].