Задачи и дополнения
1. Укажем наиболее простой способ построения матриц Адамара сколь угодно больших порядков. Пусть Нn - матрица Адамара порядка n и -Нn - матрица с противоположными элементами. Составим из них матрицу порядка 2n следующим образом:
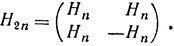
Именно таким образом получались одна из другой матрицы порядков 1, 2, 4, 8, приведенные в начале этого параграфа.
Доказать, что матрица Н2n является матрицей Адамара.
2. Следующие две операции преобразуют матрицу Адамара снова в матрицу Адамара:
1) перестановка строк (или столбцов);
2) умножение строки (или столбца) на -1.
С помощью этих операций любую матрицу Адамара можно преобразовать в так называемую нормализованную матрицу Адамара, у которой первая строка и первый столбец состоят из одних единиц.
3. Докажем, что если H - матрица Адамара порядка n > 2, то n кратно 4.
Действительно, можно считать матрицу Н нормализованной матрицей Адамара. Переставляя ее столбцы, всегда можно добиться, чтобы первые три строки матрицы имели вид:
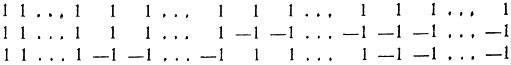
Получается четыре типа столбцов. Пусть i, j, k, l означают соответственно число столбцов первого, второго, третьего и четвертого типов. Свойство ортогональности строк влечет тогда также равенства:
i + j - k - l = 0,
i - j + k - l = 0,
i - j - k + l = 0.
Кроме того,
i + j + k + l = n.
Из этих равенств получаем i = j = k = l = n/4, откуда и следует наше утверждение.
4. Изложим еще один метод построения матрицы Адамара - метод Пэли. Рассмотрим поле Zр вычетов по модулю р, где р - простое число. Всякий элемент Zp, являющийся квадратом какого-либо элемента того же поля, называется квадратичным вычетом, всякий другой - квадратичным невычетом. Определим на Zp следующую функцию χ‾(i), называемую символом Лежандра *):
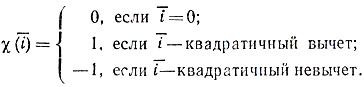
*) (Адриен Мари Лежандр (1752-1833) - французский математик, плодотворно работавший в теории чисел и в ряде разделов математического анализа и механики.)
Исходя из этого определения, можно доказать, что для всякого с ≠ 0 выполняется равенство
χ(1‾) χ(‾1 + ‾c) + χ(2‾) χ(‾2 + ‾c) + ... + χ(p-1)‾ χ (p-1‾ + c‾) = -1. (3)
Рассмотрим теперь квадратную матрицу Q порядка р, элементы которой qij (i, j = 1, 2, ..., р) определяются следующим образом:
qij = χ(j‾ - i‾).
Пусть Е - единичная матрица порядка р, a J - квадратная матрица того же порядка, все элементы которой равны 1. Тогда, пользуясь (3), можно доказать равенства
QQT = pE - J, QJ = JQ = 0. (4)
Пусть теперь p = 4k - 1. В этом случае матрица
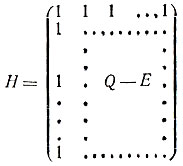
является матрицей Адамара порядка p + 1. Действительно, вычисляя произведение ННТ, получаем:
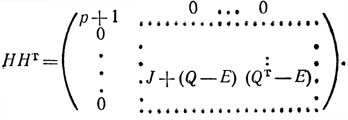
Далее, как нетрудно проверить, матрица Q порядка р = 4k - 1 совпадает с матрицей -QT. Отсюда с учетом (4) имеем:
J + (Q - E) (QT - E) = J + QQT - Q - QT + E = J + pE - J - Q + Q + E = (p + 1)E.
Таким образом, HHT = (р + 1)E.
5. В качестве примера построим матрицу Адамара порядка 8. При этом р = 7. Функция χ(i) задается следующей таблицей:
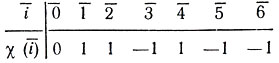
Матрицы Q и Н имеют тогда вид:

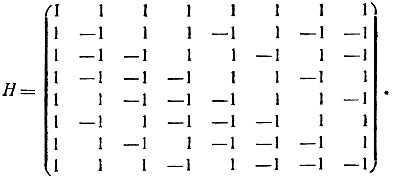
6. Построить методом Пэли матрицу Адамара порядка 12 и найти соответствующие коды Адамара.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'