6. Задачи и дополнения
1. Покажите, что преобразование, обратное параллельному перенесу в направлении вектора а, есть параллельный перенос в противоположном направлении (на вектор -а),
2. Пусть f - симметрия плоскости относительно оси Ox, g - поворот плоскости на π/2 против часовой стрелки. Проверьте, что преобразование fg есть симметрия относительно биссектрисы 1-го и 3-го координатных углов. Найдите также преобразование gf и убедитесь, что fg ≠ gf.
3. Операция произведения преобразований обладает свойством ассоциативности, это значит, что для любой тройки преобразований f1, f2, f3 выполняется равенство
(f1f2)f3 = f1(f2f3).
Справедливость соотношения вытекает из того, что обе его части есть результат последовательного выполнения трех преобразований сначала f1, затем f2, затем f3.
4. Какие из следующих множеств образуют группу преобразований плоскости:
а) множество всех параллельных переносов;
б) множество всех вращений относительно фиксированного центра;
в) множество всех вращений плоскости;
г) множество всевозможных осевых симметрии.
5. Напомним, что совокупность всех подстановок n-элементного множества образует группу. Она называется симметрической группой степени n и обозначается Sn. Найдите все подстановки из S3, не меняющие значения функций
а) φ1 = x1x2 + x2x3 + x1x3;
б) φ2 = (x1 - x2) (x1 - x3) (x2 - x3).
Проверьте прямым вычислением, что найденные в каждом из случаев подстановки образуют группы.
6. Транспозицией называется подстановка, переставляющая какие-либо два символа, а все прочие оставляющая на месте. Например, из двух подстановок


первая является транспозицией, вторая - нет, но она может быть представлена в виде произведения транспозиций следующим образом:
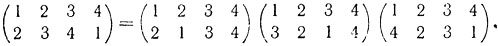
Справедлив общий факт: всякая подстановка разлагается в произведение транспозиций.
Это разложение неоднозначно, например, вместо (1) мы могли бы написать
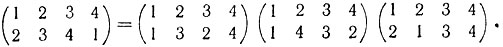
Однако можно доказать, что при всех представлениях подстановки в виде произведения транспозиций число сомножителей имеет одинаковую четность.
Подстановка называется четной, если число транспозиций и в разложении четно, в противном случае подстановка называется нечетной.
7. Покажите, что множество всех четных подстановок образует группу, она обозначается Аn и называется знакопеременной группой.
8. Убедитесь, что множество подстановок из задачи 5 (б) совпадает со знакопеременной группой A3.
Вообще рассмотрим функцию
F(х1, х2, ..., xn) = ∏i<j (xi + xj), i, j, = 1, 2, ..., n. (2)
Тогда множество всех подстановок переменных, не меняющих значения этой функции, совпадает со знакопеременной группой Аn. Это вытекает из того, что при любой транспозиции значение функции (2) меняется на противоположное, например,
F(х1, х2, ..., xn) = -F(х1, х2, ..., xn).
Сказанное объясняет и происхождение термина "знакопеременная группа".
9. Для числовых групп типичной является такая ситуация, когда все степени одного элемента g ≠ 1 различны *). Если же обратиться к группам преобразований, то в них зачастую бывает так, что две различные степени одного элемента (преобразования) совпадают. В качестве примера таких элементов рассмотрите преобразования: а) симметрию относительно оси; б) поворот плоскости на угол π/3 (вообще на угол 2π/k).
*) (В случае, если групповая операция - сложение, приходится говорить не о степенях, а о кратных элемента.)
Что касается конечных групп, то здесь для любого элемента g существуют такие натуральные k и m (k ≠ m), что
gk = gm. (3)
Если бы это было не так, то группа содержала бы бесконечно много элементов.
Пусть в равенстве (3) к > m. Умножим обе его части на элемент g-m, это даст следующее равенство gk-m = e, или gn = e, где n = k - m > 0.
В описанной ситуации обязательно найдется наименьшее натуральное n со свойством gn = e, которое называется порядком элемента g.
Если же все степени элемента g
g0 = e, g, g2, ..., gk
различны, то g называется элементом бесконечного порядка.
10. Найдите порядки следующих подстановок:
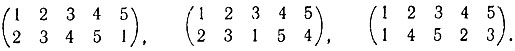
11. Пусть G = (g) - конечная циклическая группа, и ее образующий g имеет порядок n. Рассмотрим произвольную степень gm.
Если показатель кратен n(m = sn), то gm = gns = (gn)s = es = e. Если же показатель m произволен, то его всегда можно записать в виде: m = sn + r, 0 ≤ r ≤ n-1, где r - остаток от деления m на n. Но тогда gm = gsn+r = gsn · gr = e · gr = gr. Это значит, что все элементы группы G = (g) исчерпываются следующими n элементами:
е, g, g2, gn-1.
Мы доказали, что порядок конечной циклической группы совпадает с порядком ее образующего. Как, используя сказанное, вывести из теоремы Лагранжа следующие утверждения:
а) порядок любого элемента конечной группы является делителем порядка этой группы;
б) всякая группа простого порядка является циклической?
12. Найдите возможные порядки элементов в группах S3, S5, циклической группе порядка 12.
13. Проверьте, что всякая подгруппа Н циклической группы G = (g) сама является циклической.
Указание: рассмотрите наименьшую положительную степень gk ∈ H, покажите, что H = (gk).
14. Покажем, пользуясь законом дистрибутивности, что нулевой элемент аддитивной группы кольца играет роль нуля и при умножении.
Рассмотрим произведение любых двух элементов а и b и преобразуем его следующим образом:
ab = (a + 0) b = ab + 0b.
Второе слагаемое, как видно из равенства, играет роль нейтрального элемента при сложении. В силу его единственности 0b = 0 для всякого b ∈ K.
15. Какие из следующих числовых множеств являются кольцами относительно обычных операций сложения и умножения:
а) множество четных чисел;
б) множество чисел, кратных данному n;
в) множество многочленов степени ≤ n с действительными коэффициентами;
г) множество всех многочленов с целыми коэффициентами;
д) множество неотрицательных действительных чисел;
е) множество всех чисел вида а + b √2, где а и b - рациональные.
В каких случаях мы имеем дело с кольцом с единицей, в каких - с полем?
16. Покажем, что делитель нуля (левый или правый) не может быть обратим. В самом деле, пусть ха =1 и ab = 0. Тогда
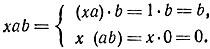
Следовательно, b = 0 и а не является делителем нуля.
Из сказанного непосредственно вытекает, что никакое поле не содержит делителей нуля.
17. Показать, что если n= n1 · n2 - число составное, то Zn не является полем.
18. Показать, что ненулевой элемент k‾ ∈ Zn обратим тогда и только тогда, когда числа k и n взаимно просты, и что в противном случае k‾ является делителем нуля.
19. Пользуясь предыдущим утверждением, найдите обратимые элементы и делители нуля в кольцах вычетов Z6, Z8, Z11, Z12. Для обратимых элементов найдите обратные. Для элементов k‾, являющихся делителями нуля, найдите m‾ ≠ 0 такой, что k‾ m‾ = 0‾. Является ли такой класс m единственным?
20. Уже самые простые сведения о кольцах и группах могут быть применены в различных математических вопросах. Прекрасной иллюстрацией этого является теория чисел. Рассмотрим, например, хорошо известную теорему (малую теорему Ферма):
Если р - простое, то для любого натурального а число ар - а делится на р.
Рассуждаем так:
ар - а = а (aр-1 - 1).
Если а делится на р, то утверждение очевидно.
Пусть а не делится на р и а = mр + r (0 < r ≤ р-1). Тогда в поле вычетов Zр а ∈ r‾ и r‾ ≠ 0. Делимость числа аp-1 - 1 на р равносильна тому, что в Zр справедливо равенство ‾rp-1 - 1‾ = 0 или равносильное ему
‾rp-1 = 1‾. (4)
Так как порядок мультипликативной группы поля Zp равен р-1, то из теоремы Лагранжа вытекает справедливость равенства (4), и это доказывает малую теорему Ферма.
21. Подумайте (это не простая задача), как с помощью указанных методов можно доказать утверждение: если р - простое, то (р-1)! + 1 делится на р. Это теорема Вильсона, одна из наиболее изящных теорем элементарной теории чисел.
22. Функция Эйлера φ(n) определяется в теории чисел как количество натуральных чисел, меньших п и взаимно простых с ним. Например, φ(4) = 2, φ(8) = 4 и т. д. Для всякого простого р очевидно φ(р) = р - 1. Обобщением малой теоремы Ферма является теорема Эйлера, которая формулируется так:
Для любого натурального а, взаимно простого с n, aφ(n) - 1 делится на n. Например, при n = 8, а = 5 имеем 54 - 1 = 624 = 8 × 78. Можно предложить следующий план доказательства теоремы Эйлера (детали - на усмотрение читателя):
а) показать, что множество обратимых элементов любого кольца образует группу относительно умножения;
б) рассмотреть кольцо вычетов Zn и убедиться, что группа его обратимых элементов имеет порядок φ(n) (вспомните утверждение пункта 18);
в) дальнейшие рассуждения таковы же, как и при доказательстве малой теоремы Ферма.
23. Найти все решения системы линейных уравнений
x + 2z = 1, y + 2z = 2, 2х + z = 1
в поле вычетов; а) по модулю 3; б) по модулю 5.
24. Многочлен р(X) ∈ F[X] называется неприводимым, если не существует разложения р(X) = f(X) g(X), в котором f(X), g(X) ∈ F[X] и степени сомножителей меньше, чем степень многочлена р(X).
Выяснить, являются ли следующие многочлены:
Х3 + Х2 + 1, Х4 + Х2 + 1, Х2 - 2
неприводимыми над полем: а) Z2; б) Z3; в) Q; г) R.
25. Разложить на неприводимые множители многочлен
Х4 + Х3 + Х + 1
над полем: a) Z2; б) Z3; в) Q.
26. Найти наибольший общий делитель многочленов
f(Х) = Х3 + Х2 + 2Х + 2; g(X) = X2 + X + 1;
над полем: а) Z3; б) Q.
27. Доказать что в конечном кольце с единицей любой ненулевой элемент либо обратим, либо является делителем нуля. Верно ли это утверждение без предположения конечности (вспомните кольцо Z)?
28. Используя предыдущее утверждение, докажите, что конечное коммутативное кольцо без делителей нуля, содержащее более одного элемента, является полем.
29. В вопросах, связанных с решением систем линейных уравнений, особую роль играет понятие определителя квадратной матрицы.
Введем здесь это понятие применительно к матрице 2-го порядка
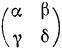
с элементами из произвольного поля F. Ее определителем называется величина
Δ = аδ - βγ. (6)
Доказать, что в кольце всех матриц 2-го порядка матрица (5) обратима тогда и только тогда, когда ее определитель отличен от нуля (указать способ отыскания обратной матрицы). В противнем случае матрица (5) является делителем нуля.
30. Какие из перечисленных ниже матриц обратимы или являются делителями нуля
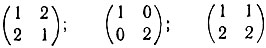
над полем: а) Z3; б) Q ?
В случае, если матрица обратима, найти обратную.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'