Автоматизация формальной логики

Хотя опыты по созданию машин, на которых можно было бы решать простейшие логические задачи, имели место начиная с конца XVIII века (напомним хотя бы известную машину С. Джевонса), широкое научное и, в достаточно близкой перспективе, практическое значение работы в этом направлении приобрели лишь в 50-х годах нашего столетия, - тогда, когда в распоряжении ученых оказался не только мощный аппарат современной логики, но и быстродействующие ЭВМ. С конца 50-х годов в разных странах мира начались работы по созданию алгоритмов (и соответствующих этим алгоритмам машинных программ), позволяющих автоматически находить логические выводы, ведущие к обоснованию некоторого предложения (данной теории) , - обнаруживать доказательства теорем логики и математики.

Известно, что открытие новых истин в процессе логического доказательства сводится к нахождению вывода гипотезы из ранее известных истин, т. е. к открытию отношения логического следования доказываемого предложения из положений, истинность которых принята либо доказана ранее. Первые значительные результаты по проблеме поиска логического вывода в нашей стране были получены в 60-х годах группой ленинградских ученых, возглавлявшейся Н. А. Шаниным.

Корректная постановка и решение проблемы поиска (дедуктивного) вывода возможна лишь для формализованных теорий. При построении такого рода теории используется: формализованный язык, аксиомы теории и аппарат правил логического вывода. Поэтому при решении проблемы поиска вывода надо прежде всего располагать точным языком выражения соответствующих задач. В качестве такого языка был выбран язык классического исчисления предикатов (узкого: без кванторов по предикатам), включающий в себя, как известно, язык классического исчисления высказываний. Задача поиска вывода ставилась применительно к теориям математики. Известно, что не все математические теории могут быть выражены на указанном языке; однако на нем может быть выражена всякая конечно-аксиоматизируемая теория (т. е. теория, которая может быть задана конечным списком аксиом) , - а большинство существующих математических теорий именно таковы. Поэтому, если список аксиом (схем аксиом) теории конечен, поиск вывода в ней может быть сведен к поиску вывода в узком исчислении предикатов.

В качестве аппарата логического вывода использовался аппарат формального вывода, разработанный в математической логике. Алгоритм поиска логического вывода - это регулярная процедура, которая осуществляет следующее: если формула выводима из данных посылок (или доказуема, т. е. выводима из пустого множества посылок), то алгоритм применим к ней и не просто выдает ответ "да", но и строит соответствующий вывод (алгоритм, который может выдавать только ответ "да" или "нет", но не строить вывод, был назван алгоритмом "оракула") ; если же формула не выводима (не доказуема) в исчислении, то алгоритм либо выдает отрицательный ответ, либо работает неограниченно долго.

Алгоритм, выдающий вывод, похожий на обычный содержательный, Н. А. Шанин назвал алгоритмом "интеллектуального партнера". Он должен был дополнить "оракул" построением естественных выводов. Это делается для того, чтобы человек мог общаться с машиной на понятном для него языке. Допустим, человек не может решить какой-либо задачи; если в его распоряжении есть "оракул", он сможет "запросить" его и узнать, скажем, что проблема решается положительно; однако в чем состоит само решение, останется для него неизвестным. "Интеллектуальный партнер" же не только выдает решение, но предъявляет его в форме, соответствующей ходу содержательного мышления человека. Машина, запрограммированная в соответствии с алгоритмом поиска естественного вывода, может помочь человеку разобраться, в чем состоит трудность, - обнаружить, что не додумал человек, когда решал задачу. Этим и объясняется название: "интеллектуальный партнер". Существенно, что, решая задачу, этот "партнер" не только выводит проверяемую формулу, но и строит ведущий к ней фрагмент формализованной теории - и среди этого фрагмента могут оказаться, в принципе, интересные новые теоремы.

Разумеется, при построении "интеллектуального партнера" мы связаны жестче, чем в случае просто поиска (какого-то) логического вывода. Но на уровне исчисления высказываний задача от этого не делается намного сложнее. Построение "интеллектуального партнера" группой Н. А. Шанина осуществлялось для классического исчисления высказываний. Это - необходимый шаг для подхода к построению алгоритма поиска естественного вывода для исчисления предикатов. Уже для классического узкого исчисления предикатов задача становится существенно более трудной; однако, смотря на проблему с современных позиций, мы сможем сказать, что эти трудности преодолимы, и алгоритм поиска естественного вывода в исчислении предикатов может быть сделан достаточно компактным и обозримым.

Машинная реализация алгоритма - это были 60-е годы - осуществлялось на ЭВМ типа "Урал-4". Вывод, который писала машина на бумажной ленте, представлял собой текст, составленный из некоторых фраз русского языка ("Задача: вывести из исходных формул ... формулу ...", "Допустим, что ..." и т. п.) и выражений символического языка исчисления высказываний. В работе [83] Н. А. Шаниным и его соавторами описывается решение на ЭВМ следующей проблемы: если задан какой-либо список формул исчисления высказываний Q₁, Q₂,..., Q_n и еще какая-либо формула исчисления высказываний R, то необходимо составить алгоритм, выясняющий, выводима ли формула R из Q₁, Q₂, ..., Q_n логическими средствами классического исчисления высказываний (т. е. выводима ли формула R в исчислении, получаемом в результате присоединения к классическому исчислению высказываний формул Q₁, Q₂,... , Q_n в качестве дополнительных исходных формул) , и при утвердительном ответе на этот вопрос искомый алгоритм должен строить (и это в проблеме главное) естественный вывод R из Q₁, Q₂,...

При построении алгоритмов логической дедукции можно пользоваться исчислениями различного типа: аксиоматическими (так называемыми исчислениями гильбертовского типа), натуральными (восходящими к работам Г. Генцена), секвенциальными (впервые построенными тем же Генценом). Алгоритмы, разрабатывавшиеся в группе Н. А. Шанина и доложенные в 1964 г. на I Всесоюзном симпозиуме по проблеме машинного поиска логического вывода в г. Тракай Литовской ССР, основывались на секвенциальных исчислениях. Но на том же симпозиуме С. А. Яновская показала, что для целей поиска вывода можно использовать иной логический аппарат, а именно аппарат так называемых таблиц Бета. Этому вопросу она посвятила два доклада. Первый назывался "Некоторое уточнение алгоритма перевода семантических таблиц Бета в дедуктивные и дедуктивных в натуральный вывод". Семантические таблицы, предложенные, голландским математиком и логиком Э. Бетом, представляют собой, по существу, определение понятия логического следования или секвенции, согласно которому заключение является логическим следствием из данных посылок, если нельзя сделать посылки истинными, а заключение ложным. В семантических таблицах Бета фактически заключен алгоритм "оракул", - как для исчисления высказываний, так и для узкого исчисления предикатов. В дополнении Бета в его книге "Формальные методы" содержится указание, что с помощью семантических таблиц можно получить вывод данной формулы в натуральном исчислении, но не дано необходимых указаний о том, как это можно сделать. Ответ на этот вопрос и дала С. А. Яновская. Она показала, как по семантическим таблицам, представляющим вывод некоторой формулы из данных посылок, можно, используя определенные правила, получить вывод в так называемых дедуктивных таблицах Бета, а на основании последних построить линейный вывод в натуральном исчислении. Так получается алгоритм "интеллектуальный партнер". В своем втором докладе С. А. Яновская рассказала о решении проблемы разрешения - о построении алгоритма, распознающего как выводимость, так и невыводимость формулы для конструктивного (без закона исключенного третьего) исчисления высказываний с помощью семантических таблиц Бета.

Аппарат таблиц Бета логически очень прозрачен и дает возможность проиллюстрировать механизм поиска логического вывода, не прибегая к выписыванию формул громоздкого формализма. Суть метода состоит в том, чтобы показать, что заключение R не может быть ложным при истинности посылок Q₁,..., Q_n Пусть знаки &, V, ⊃ и
означают, соответственно, логические союзы "и" (конъюнкция), "или" (неразделительная дизъюнкция), "если ... , то" (импликация) и "не" ("неверно, что"; отрицание). Приняв обычные для классической логики определения операций, представляемых этими знаками, а именно, считая: что формула (высказывание) Ф₁ & Ф₂ истинна тогда и только тогда, когда истинно как высказывание Ф₁ , так и высказывание Ф₂; что формула Ф₁ V Ф₂ ложна тогда и только тогда, когда и Ф₁, и Ф₂ ложны; что формула Ф₁ Э Ф₂ ложна тогда и только тогда, когда Ф₁ истинна, а Ф₂ ложна (что равносильно тому, что формула Ф₁ ⊃ Ф₂ истинна, когда Ф₁ ложна или Ф₂ истинна) ; и что формула
Фистинна, когда Ф ложна, и
Фложна, когда Фистинна, мы получаем следующий метод опровержения формул упомянутого вида (под опровержением формулы понимается обоснование ее ложности): для опровержения конъюнктивной формулы достаточно опровергнуть ее первый или ее второй член; для опровержения дизъюнктивной формулы требуется опровергнуть оба ее члена; для опровержения импликативной формулы надо, приняв Ф₁ (антецедент), опровергнуть Ф₂ (консеквент); для опровержения формулы
Ф₁ достаточно обосновать формулу Ф₁.

В "ложностной" ее части стоит формула
(А & В); значит, в "истинностной" части должна появиться формула А & В. Поскольку конъюнктивная формула верна лишь при условии верности обоих ее членов, мы в той же части должны записать формулы А и В. Теперь займемся формулой (2). Она стоит в колонке +1.1, т.е. признается истинной (это посылка). Но дизъюнктивная формула истинна, когда истинен по крайней мере один из ее членов. Значит, надо рассмотреть случай истинности как формулы
А, так и формулы
В. Это приводит к расщеплению табл. 1.1 на подтаблицы 1.1.1 и 1.1.2. Формула
А записывается в колонке +1.1.1, а формула
В - в колонке +1.1.2. Рассмотрим подтаблицу 1.1.1. В обеих ее частях - "истинностной" и "ложностной" - стоит формула А. Значит, эта подтаблица замыкается. Замыкается и таблица 1.1.2 (так как формула В оказывается и в колонке +1.1.2, и в колонке -1.1.2, что означает противоречие). Итак, во всех таблично представленных случаях мы приходим к абсурду. Значит, формулу С нельзя сделать истинной при истинности данных посылок, т. е. она из них логически следует.

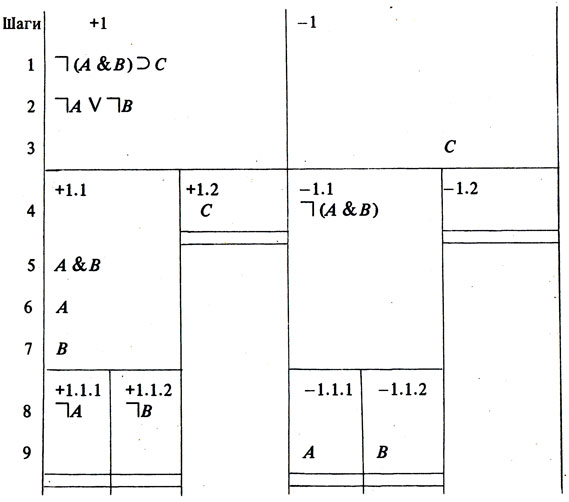
Таблица 1

Ясно, что описанный процесс рассуждения (построения таблицы Бета) носит совершенно регулярный (алгоритмический) характер. Как показала С. А. Яновская, на основе такой - семантической - таблицы регулярным же способом можно построить натуральный (естественный) логический вывод, ведущий от посылок к искомому заключению (более подробно связанные с этим вопросы рассмотрены в книге О. Серебрянникова [84]).

Уже сейчас некоторые аспекты задач поиска вывода имеют близкое отношение к практике. С автоматическим реферированием связана, например, разработка следующей проблемы: уметь узнать, содержит ли реферируемая статья нечто новое или она повторяет уже имевшиеся публикации. Для конечно-аксиоматизируемой теории имеет смысл требование определения того, можно ли построить в ней вывод, длина которого не больше установленного заранее числа шагов. Эта задача связана не только с моделированием элементов творчества (построение цепочки вывода), но и с модельным представлением более "рутинной" деятельности - восприятия и осмысления работы, выполненной другими: с автоматизацией составления реферативных "выжимок" научных, текстов, причем в применении не только к математическим, но и иным областям знания. Примером другой проблемы может служить задача вылавливания "дырок" в доказательствах; под дыркой при этом понимается ситуация, когда фигурирующее в доказательстве предложение не следует из других ранее полученных предложений того же доказательства менее чем за фиксированное число шагов.

Важной является проблема построения алгоритмов поиска вывода новых нетривиальных теорем, начиная с уровня логики высказываний и предикатов. Еще в 1960 г., до работ группы Н. А. Шанина, Хао Ван опубликовал статью [85], в которой описывался алгоритм порождения теорем исчисления высказываний, не известных ранее. Но предложенный им путь представляется мало интересным, так как в его алгоритме большую роль играл случай. Н. А. Шанин и его сотрудники в 60-х годах выдвинули идею другого пути; суть его, грубо говоря, можно описать так. Представим себе, что некоторая формула не выводима из данных посылок. Тогда ставится задача так "подправить" эту формулу, чтобы она из этих посылок стала выводимой; другая задача: в целях достижения выводимости данной формулы из данных посылок произвести соответствующее "подправление" посылок. Естественно возникает и такая задача. Пусть известно, что некоторое заключение следует из некоторых посылок; спрашивается, нельзя ли ослабить посылки, но сохранить указанную выводимость; и нельзя ли из данных посылок вывести формулу, более сильную, чем первоначальная.

В последние годы в Институте кибернетики АН УССР под руководством В. М. Глушкова шла разработка оригинальной методологии автоматизации дедукции [58]. Прежде всего решается задача построения практически-ориентированного языка математической логики, при помощи которого можно оперировать крупными "блоками" доказательств. Кроме того, в этом языке предусматривается введение средств определения новых понятий и порождения (конструирования) тех или иных общих соотношений.

Далее, от машины требуется, чтобы она не угадывала конструкции, а на основе применения логического аппарата, использующего крупные блоки дедуктивных выводов, которые заложены в ранее доказанные теоремы, по готовой конструкции проверяла, удовлетворяет ли она тем или иным свойствам (так называемый "алгоритм очевидности"). В перспективе реализация алгоритма очевидности на конкретной информационной базе, считают украинские кибернетики, откроет путь такой перестройки "здания" математики, что все оно со временем будет покоиться "на вполне понятном, объективированном, едином, универсальном понятии очевидности" [58, с. 307]. Это повлечет много практических применений. Среди них - объективный контроль за пониманием изучаемого материала учащимися-математиками, организация автоматической проверки правильности новых научных (в данной области математики) результатов; новая система организации справочно-информационной службы (например, возможен существенно содержательный ответ, состоящий в том, что, хотя запрашиваемый факт машине не известен, он является "очевидным" следствием из таких-то фактов).

Одним из наиболее интересных свойств подобной развитой системы должен явиться эффект целостности. В развитии системы могут участвовать десятки или сотни крупнейших специалистов в своей области; система накопит и разложит "по полкам" (используя алгоритм очевидности) все новое и рациональное, что внес каждый из них; в результате, накопится множество проблем, которые никто из людей в отдельности решить не может, а машина может. В этом и заключается "эффект целостности" информационнр-вычис-лительной системы, созданной на базе ЭВМ: каждый из тысячи специалистов, "начинявших" систему информацией, нечто не знает, а она "знает". В этом смысле подобный информационно-вычислительный комплекс явится неким "концентратом" коллективной мудрости.

Из зарубежных работ, относящихся к машинному логическому выводу, в свое время известность получили исследования А. Ньюэлла, Дж. Шоу и Г. А. Саймона [86] и упоминавшаяся выше работа Хао Вана. Ньюэлл с коллегами еще в 1957 г. при помощи разработанной им программы "Логик-теоретик" (сокращенно ЛТ) на ЭВМ ИВМ-704 получил доказательства 38 из первых 52 теорем известного труда А. Н. Уайтхеда и Б. Рассела Principia mathematica; блок-схемы и принципы построения ЛТ неоднократно рассматривались в специальной и популярной литературе (см., например, [40, 41, 87]). Хао Ван составил три программы для доказательства теорем математической логики (реализовавшиеся на ЭВМ того же типа). Первая из них позволила машине за 37 минут доказать более двухсот теорем из первых пяти глав упомянутого труда Уайтхеда и Рассела, причем непосредственно на счет ушло только три минуты машинного времени (остальное время было затрачено на ввод-вывод данных). По второй программе машина образовывала из исходных символов предложения исчисления высказываний и выбирала из них новые - "нетривиальные". По этой программе машиной было построено и проверено в течение часа около 14000 предложений, причем было выдано на печать около тысячи теорем. Наконец, по третьей программе было доказано более ста пятидесяти теорем следующих пяти глав Principia mathematica, относящихся к исчислению предикатов с равенством. В течение часа машина нашла доказательства для 85% этих теорем [85]. По крайней мере в одном случае машина выдала доказательство теоремы из второй главы, которое оказалось стройнее и короче, чем приведенное Уайтхедом и Расселом^*.

^* (Встречающиеся в популярной печати сообщения об имевшем якобы месте машинном доказательстве множества новых интересных теорем следует полагать вымышленными.)

В свое время авторы программы ЛТ высказали мнение, что машина, работающая по этой программе, может не только доказывать теоремы, но и выдвигать "новые задачи", что она может формулировать новые предложения соответствующего формального языка и "стремиться" к их доказательству [41]; аналогично этому, и Хао Ван показал, что ЭВМ в состоянии не только строить доказательства вводимых в нее теорем, но и формулировать сами теоремы, отбирая при этом их на "нетривиальность". Соответствующий путь в принципе прост: задать критерий нетривиальности, и тогда машина сможет выбирать и выдавать на печать теоремы, ему удовлетворяющие; на некотором этапе многократного построения этой процедуры можно будет, как считал Хао Ван, получить доказательства большого числа новых нетривиальных теорем [85, с. 127]. Исследования последующих десятилетий однако показали, сколь непросто сформулировать достаточно эффективный критерий нетривиальности. Подводя итог опыту работы в данном направлении, В. М. Глушков указал на принципы самоорганизации как на тот путь, который ведет к разработке машинных процедур отбора новых, подлинно нетривиальных теорем и их доказательств (см. [88, с. 57]).

Эксперименты по машинному выводу теорем не ограничиваются рамками математической логики. За рубежом одной из первых "нелогических" программ такого рода была программа доказательства теорем простейшего раздела геометрии [41]. В нашей стране, помимо достижений в разработке машинных программ дедуктивной логики, получены интересные результаты в автоматизации логико-вычислительных процессов алгебре (в частности, в теории групп), прикладной математике и др. Соответствующий обзор можно найти в брошюре [88]. В ней, в частности, отмечается значение работ по созданию теоретического аппарата, представляющего собой специальные логико-математические исчисления и процедуры поиска вывода в них. Наиболее крупными результатами здесь были: разработка С. Ю. Масловым так называемого "обратного метода" [89, 90] и создание Дж. Робинсоном "метода резолюций" (об этом методе см., например, [45]). "Большинство существующих сейчас программ поиска доказательств основывается на одном из этих методов... метод резолюций предназначен для установления выводимости теорем в исчислении предикатов. Обратный метод имеет более широкую область применения. Работы С. Ю. Маслова послужили теоретической основой для специальной программы, которая не только строит вывод формулы, если он может быть построен, но и в некоторых случаях дает ответ, что формула невыводима" [88, с. 58].

Все, сказанное нами, подтверждает вывод: "Формализация, по-видимому, обещает, что машины будут делать значительную часть работы, занимающей сейчас время математиков-исследователей" [41]. Не будем, тем не менее, забывать о том, что решаемые современными машинами дедуктивно-математические задачи еще достаточно просты; что осуществление машинного вывода нередко "наталкивается на совершенно непреодолимые размеры вывода (количества порождаемых резольвент в случае программ, например, основанных на методе резолюций). Это, в частности, связано с тем, что несмотря на все-таки очень большое быстродействие ЭВМ и достаточно большие объемы памяти, время решения задачи исчисляется десятками суток непрерывной работы машины; памяти также не хватает" [88, с. 55].

Но не будем забывать слова двух других крупных математиков: "Между работой ученика, решающего задачу по алгебре или геометрии, и изобретательской работой разница лишь в уровне" (Ж. Адамар, [91, с. 98]); "Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия" (Д. Пойа, [92, с. 5]). В другой работе [93] Пойа, пытаясь определить, что значит решить задачу, поясняет, почему он в решении каждой из них видит элемент открытия: "Задача предполагает необходимость сознательного поиска соответствующего средства для достижения ясно видной, но непосредственно не доступной цели. Решение задачи означает нахождение этого средства" (с. 143).

Автоматизация логического вывода не случайно явилась одним из первых направлений кибернетических исследований. Закономерность этого явления вытекает, по-видимому, из тезиса, сформулированного Б. Расселом в следующей форме: "всякое математическое мышление, в принципе, может быть механически истолковано как манипуляция символами согласно предписанным правилам, некое подобие шахматной игры" (цит. по [94, с. 14]) - с добавлением указания на необходимость плодотворных эвристик, позволяющих находить такое истолкование. Именно соединение дедукции с эвристически направляемым поиском (о котором речь пойдет ниже) делает убедительным рассуждение В. М. Глушкова, который в одном из своих докладов сказал, что ныне математик, кончая творческую жизнь, оставляет потомкам некоторое число доказанных им теорем; однако настает время, когда можно будет оставлять не отдельные теоремы, а программы, каждая из которых при помощи ЭВМ будет порождать классы новых "теорем.