Дедуктивная и недедуктивная эвристика

В связи с проведенными выше рассмотрениями возникает вопрос о различении ступеней "эвристического", "творческого", "сложного" и т. п. в применении к задачам кибернетического моделирования и ИИ. Один из возможных подходов уже излагался авторами этих строк [58]. Заключается он в следующем. Выделяются дедуктивная и недедуктивная эвристики (причем последняя рассматривается в качестве эвристики в собственном смысле). Отличительный признак первой - в том, что будучи эвристикой в том плане, что соответствующая программа приводит (или, лучше сказать, может приводить) к результатам, которые можно признать в определенном смысле "творческими", реализуется она с помощью "обычных" вычислительных алгоритмов или алгоритмов, им аналогичных. Примером осуществления такой эвристики могут служить упоминавшиеся выше программы Хао Вана, дающие ответ относительно доказуемости некоторой формулы. Формальные выражения, проверяемые этими программами на доказуемость (выводимость) могут быть очень сложными, никогда не выписывавшимися и не выводившимися человеком и, значит, новыми. Но сам процесс проверки (вывода) принципиально не отличается от решения обычной вычислительной задачи.

Дедуктивная эвристика может имитировать определенный круг рассуждений человека. Такой характер носили, например, программы, создававшиеся коллективом математиков, возглавлявшимся Н. А. Шаниным [83]; таковы же многие новейшие программы автоматизации дедуктивных методов, которые упоминались в предшествующем разделе. Эти программы не просто отвечают на вопрос о доказуемости поставленной на проверку формулы (или о ее выводимости из некоторых посылок), но и печатают - в случае положительного ответа на вопрос о доказуемости - ее вывод, причем последний может носить естественный, "человеческий" характер. В литературе можно найти много интересных соображений о характере тех принципов, которые должны быть заложены в алгоритм для придания выводу естественного характера. Некоторые из них выявлены в работах О. Ф. Серебрянникова [84] и С. Ю. Маслова (см. [90,95]). Для нас существенно, что такое выявление значимо для перехода уже к эвристике иного типа - к эвристике недедуктивной.

Недедуктивная эвристика отличается от дедуктивной тем, что эвристический алгоритм, в который стремятся заложить человеческие приемы открытия нового (типа тех приемов рассуждения, которые описаны в известных книгах Д. Пойа [92,93,96]), может не отражать всех свойств соответствующей массовой проблемы и потому выдавать решение не всех задач соответствующего класса (или выдавать плохое решение, или же давать ответ, который нельзя признать решением соответствующей задачи); иначе говоря, машины, реализующие такой алгоритм, могут "пасовать" перед задачей (даже если разрешить машине работать сколь угодно долго) или же "ошибаться". Таким образом, машинное "поведение" и в данном отношении напоминает человеческое, почему программу и можно назвать "собственно эвристической". Именно такой характер носили программы Ньюэлла, Шоу и Саймона - "Логик-теоретик", а потом "Решатель общих проблем". Например, ЛТ работала явно хуже, чем составленная после нее программа Хао Вана. Но, в отличие от хаовановской программы, ЛТ имитировала человеческий поиск решения.

Чего же стремятся достичь, вступая на путь создания программ "собственного эвристического" стиля? - Создания методов решения сложных задач - задач, исчерпывающее описание которых (т. е. точная постановка) затруднительно; иначе говоря, задач, для которых не все свойства охватывающей их массовой проблемы известны. Весь смысл эвристического программирования состоит в расчете: пусть простые задачи данным методом решаются хуже, чем это позволяет сделать путь дедуктивной эвристики, зато на сложных задачах, где "обычные" алгоритмы (программы) "захлебнутся" в переборе вариантов (даже при достаточно хорошо организованном движении по дереву альтернатив), программы эвристического типа, основанные на "подсмотренных" у человека приемах рассуждения, смогут (конечно, не всегда) дать приемлемое решение. Таким образом, можно сказать, что (собственно) эвристические программы полнее моделируют творческую компоненту мышления, чем методы "дедуктивной эвристики".

Таков один из способов различения разных уровней эвристичности и "творческости" применительно к системам моделирования мышления. Но возможен и другой подход, более глубоко проникающий в суть проблемы. Мы имеем в виду идеи группы специалистов и прежде всего Д. А. Поспелова, подвергших анализу соотношение эвристического программирования и эвристики как науки и предложивших классификацию задач (массовых проблем) по степени их трудности для представления в системах "искусственного интеллекта". Эта классификация основана на следующем.

Произведем, опираясь на идеи, изложенные в [61], детализацию структуры массовой проблемы (ср., например, как это понятие обычно раскрывается в монографиях по математической логике, например, в [97]) несколько иным способом. Выделим пространства исходных данных (ситуаций) U, промежуточных состояний - т. е. состояний, возникающих в ходе решения задач (его обозначим через П, - и состояний заключительных (результатов, Р). Не будем накладывать каких-либо ограничений на отношения между пространствами U, П и Р (это существенное обстоятельство!). Пусть задан некоторый набор Q элементарных операций, перерабатывающих одни состояния (из U и П) в другие. Тогда очевидно, что применение какой-то операции q ∈ Q к произвольному элементу и ∈ U породит некоторый элемент n ∈ П. Смысл массовой проблемы состоит в том, чтобы по произвольному элементу и ∈ U получить некоторый элемент р ∈ Р - результат. Такое получение может происходить с помощью лишь какого-то метода, который, коль скоро речь идет о системах, реализуемых на ЭВМ, должен носить алгоритмический характер, т. е. задаваться с помощью некоторого алгоритма α. По любой исходной ситуации и Е ∈ U алгоритм α строит последовательность операций, применение которых к соответствующим элементам из П порождает (в предположении абстракции потенциальной осуществимости) требуемый результат р ∈ Р (если алгоритм к данной исходной ситуации применим).

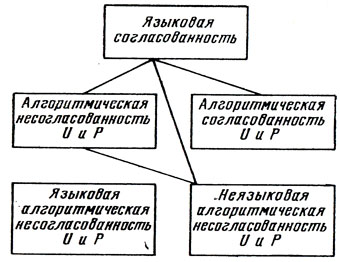
Рис. 7

Из описанной схемы нетрудно усмотреть основания для типологии задач, решаемых человеческим мышлением и моделируемых в "искусственном интеллекте", особенно если допустить операции и алгоритмы недетерминистского (вероятностного или расплывчатого в смысле 3аде) вида, ввести оценки близости состояний и достижимости заключительного состояния. Могут быть задачи, связанные с поиском необходимых операций Q, а также алгоритма α, с устранением языковой несогласованности и др. Мы не будем на этом останавливаться, а отошлем читателя к статье [61]. Задержимся только на одном пункте, со всей силой подчеркнутом Д. А. Поспеловым: на задаче перевода проблемы, для которой языковое согласование отсутствует, в проблему с требуемым языковым согласованием. Как справедливо отмечает упомянутый автор, проблемы, для которых имеется языковое согласование, могут рассматриваться как задачи поиска пути в лабиринте (быть может, бесконечном, каковым, например, является поиск доказательства произвольной формулы в узком исчислении предикатов), ведущем от некоторой начальной площадки к площадке конечной (свойства площадок описаны на общем "лабиринтном" языке). Смысл эвристического подхода в этом случае состоит в том, чтобы заменить полный перебор (обычно реально не осуществимый даже для конечных лабиринтов) усеченным перебором и целенаправленным движением по дереву альтернатив. Психологические опыты показали, что человек и животное в ряде случаев именно "лабиринтно" подходят к задачам, причем если задача - новая (свойства лабиринта, т. е. дерева альтернатив, не известны), то наблюдается некоторый период "проб и ошибок", случайный перебор и т. п. до тех пор, пока решающий не составит некоторые гипотезы о структуре дерева перебора и не выработает стратегию поиска.

Д. А. Поспелов высказал мысль, что задачи подобного рода носят нетворческий (или не очень творческий) характер и их не следует относить к "искусственному интеллекту". На этом основании он не причисляет к этому направлению, например, большинство работ по автоматизации поиска логического вывода и доказательству теорем логики и математики. С этим вряд ли можно согласиться. Ведь если следовать этому критерию, то по крайней мере часть математики выпадет из сферы творчества! Конечно, наличие языкового согласования в определенном смысле упрощает соответствующую задачу. Но ведь это не единственная характеристика трудности задач и, соответственно, не единственное их свойство, требующее от человека открытия чего-то нового. Разве доказательство трудной теоремы, уже ранее сформулированной в математике, не есть творческий акт? Можно ли было "нетворчески" построить доказательство теоремы, требующее индукции по десяткам параметров, - достижение, обычное для творчески работающих математиков?!

Но, конечно, вне математики и логики главным источником трудности задач является именно языковое рассогласование между тем, что дано, и тем, что требуется получить. Согласно идее, выдвинутой В. Н. Пушкиным и Д. А. Поспеловым, суть решения в этом случае состоит в том, что "проблемная среда", в которую погружены условия и цели, подвергается переосмыслению; если речь идет о человеке, то основным оказывается то, что он по-новому подходит к структуре среды, по-иному ее структурирует; "как только человек находит нужное структурирование, возникает "озарение" (инсайт) и проблема становится разрешимой" [61, с. 223]. В семиотико-кибернетических терминах это означает, что - коль скоро ставится задача построения модели соответствующего творческого процесса - необходимо построить новый язык, на котором описывались бы и исходные, и целевые ситуации. Создание такого языка обеспечивает необходимое языковое согласование и открывает возможность использования известных методов решения "лабиринтных" задач. "Таким образом, основным творческим актом при решении проблем при отсутствии языкового согласования является построение такой модели проблемной ситуации, в которой было бы достигнуто необходимое согласование. Такая модельная концепция значительно богаче лабиринтной и включает последнюю в качестве частного случая" [61, с. 213].

Задача моделирования проблемной ситуации для случая реализации на ЭВМ принимает вид задачи представления знаний в машинной памяти в форме большой базы данных, в которой информационные образования связаны между собой не столько за счет хорошо известных методов адресации информационных массивов и их элементов, сколько за счет отображения в структуре базы смысдовых (семантических) связей между содержащимися в ней сведениями. Соответствующие проблемы, как известно, решаются в теории информационно-поисковых систем, особенно систем, содержащих логические связи между элементами хранящейся в системах информации. Однако обеспечение языкового согласования применительно к сложным задачам, принимая форму семантического структурирования "внешней" (для машины) среды или создания внутримашинной модели "внешнего мира", приводит к серии проблем, выходящих за рамки обычной тематики информационного поиска, поскольку означает разработку формализованных аналогов человеческих познавательных процессов абстрагирования, обобщения, образования понятий и их систем, использования различных уровней абстракции и т. п.

В настоящее время в области моделирования процессов образования понятий, построения обобщенных описаний и структурирования внешней среды проводятся интересные работы, как в СССР, так и за рубежом. Представление о них можно получить из материалов IV Международной объединенной конференции по искусственному интеллекту, I и II Международных совещаний по искусственному интеллекту в Репино, V Международной конференции по искусственному интеллекту (США) и большому числу других публикаций, отечественных и зарубежных (из последних отметим, например, книгу Б. Рафаэля [98]). В работах исследователей США структурирование проблемной среды и построение обобщенных описаний производится на основе введенного М. Минским понятия "ситуационной рамки" - фрейма (краткое освещение смысла этого понятия см. в статье [78]). В нашей стране для той же цели используется, в частности, язык и методы ситуационного управления [68, 69]. Это направление исследований близко связано с работами по автоматическому распознаванию образов, но отличается от него наличием более существенной логической составляющей. В частности, здесь активно используются формализованные языки, основывающиеся на исчислении предикатов первого порядка (без кванторов по предикатам). Работы по машинному моделированию внешней среды, основанные на логико-семантических представлениях и часто связанные с созданием соответствующих средств "роботики" (ср. упоминавшиеся выше работы Т. Винограда), представляют в настоящее время один из самых важных участков "искусственного интеллекта".

Рассмотренные в настоящем разделе направления исследований открывают возможности для использования ЭВМ в качестве "технических средств" эвристики, т. е. таких средств, которые в ситуациях, когда человек перестает действовать точно, избавляют его от рассмотрения многочисленных, но не существенных деталей, что в конечном итоге может подсказать пути решения научной задачи. Вслед за формализацией логической дедукции - уже прочным завоеванием научной и технической мысли - наступает пора формализации эвристических процессов.

В заключение этого раздела поясним соотношение формализованного, эвристического и творческого при помощи двух схем, заимствованных из коллективной монографии [58] (см. схемы I, II).

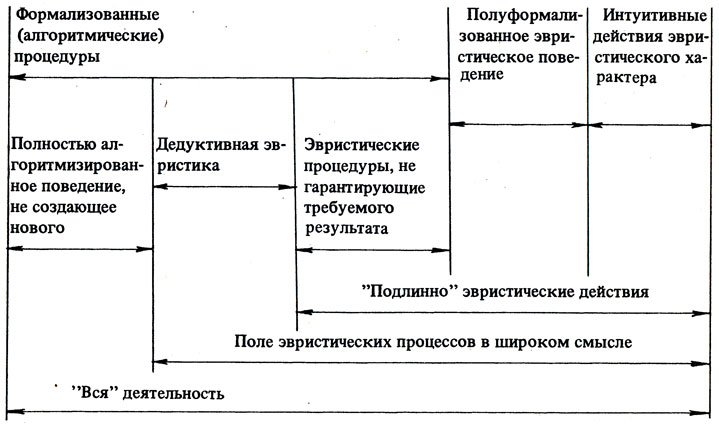
Схема I.

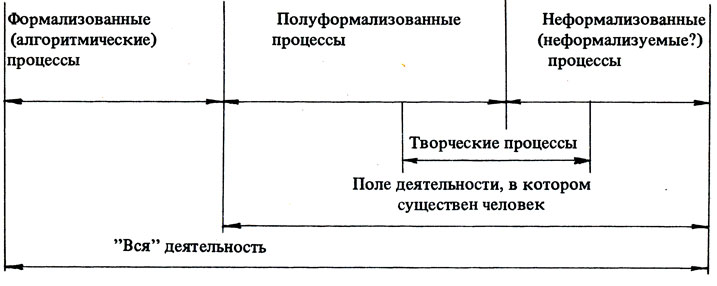
Схема II