Приложение 1. Формирование множества пучков траекторий

Б. М. Штильман

Шахматы, как известно, представляют собой конечную игру, поэтому можно дать исчерпывающее описание шахмат с помощью дерева игры. Если бы дерево не было столь катастрофически большим, то лучший ход легко определялся бы с помощью минимаксной процедуры на всем дереве игры.

Задача состоит в том, чтобы в полном дереве игры выделить для анализа такое поддерево, которое бы удовлетворяло трем требованиям.

1. В поддереве должны содержаться варианты с хорошим ходом в данной позиции.
2. Поддерево должно быть достаточно маленьким (по числу включенных в него ходов), чтобы устройство по переработке информации могло совершить все необходимые операции за приемлемое время.
3. Поддерево должно быть настолько узким, чтобы при фиксированном числе содержащихся в нем ходов варианты были достаточно длинными и устройство по переработке информации могло получить их разумные оценки и на основании этих оценок выбрать хороший ход.

Созданные к настоящему времени "технологические" программы полного перебора на фиксированную глубину, очевидно, удовлетворяют первому и второму требованиям. Третьему требованию они не удовлетворяют, так как не имеют разумного критерия обрыва вариантов, а также не могут строить глубокого дерева из-за экспоненциального роста числа вариантов. Современные программы сокращенного перебора удовлетворяют лишь требованию 2.

Основой обсуждаемой программы, позволяющей выполнить все требования, является математическое отображение (МО) - динамическая модель шахматной игры. Пусть А - множество всех допустимых правилами ходов в данной позиции; В - такое подмножество А, в котором всегда содержится хороший ход m в данной позиции: m∈B⊂A. Задача любого алгоритма неполного перебора ходов состоит в правильном выборе этого подмножества В, т. е. В действительно должно содержать хороший ход и быть небольшим. В нашей программе В - это совокупность некоторых ходов по траекториям МО.

Остановимся на вопросе о том, как создается МО и какую роль играет при этом множество пучков траекторий, а затем перейдем к описанию конкретной реализации этого множества. В исходной позиции рассмотрим пучки траекторий нападения фигур одного цвета на фигуры другого цвета, по длине не превышающие горизонт.

Полученная совокупность пучков и будет исходным множествам пучков в данной позиции. С этим багажом мы и начинаем перебор ходов. Фигуры в процессе перебора меняют свои места, начинают "видеть" в пределах горизонта другие фигуры, поэтому появляются новые пучки траекторий - формируются зоны и тем самым создается МО.

Таким образом, перебор ходов здесь используется для сбора информации о структуре зон, которая и позволит найти решение. Если в существующих программах неоптимальные варианты при переборе не дают полезной информации, то в данном алгоритме они используются при формировании зон. Итак, с одной стороны, перебор происходит по траекториям МО, с другой - МО формируется в процессе перебора.

Рассматриваемый здесь подход к алгоритмизации шахмат, в сущности, нигде не использует то, что эта игра является конечной. Методика построения поддерева игры для анализа никак не опирается на существование полного дерева игры. Принципы данного алгоритма могут быть использованы и в играх, где конечного дерева перебора не существует.

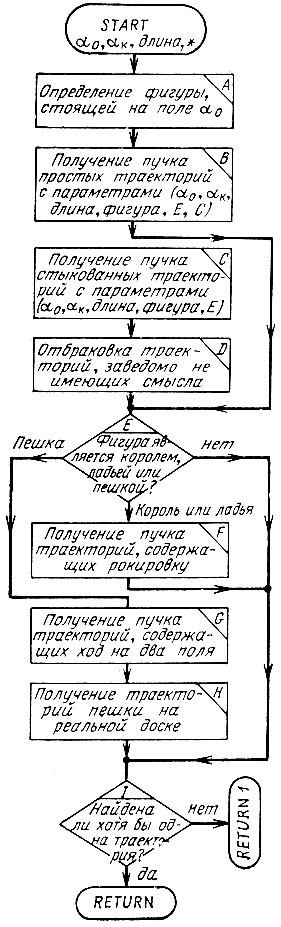
Рис. 8. Блок-схема подпрограммы получения пучка траекторий

Перейдем к описанию программы вычисления множества пучков. Прежде всего, опишем алгоритм получения пучка траекторий с α₀-поля на α_k-поле. Для того чтобы воспользоваться алгоритмом, нужно задать поля α₀ и α_k, фигуру, траектории которой мы ищем, а также длину пучка, т. е. число передвижений фигуры по траекториям этого пучка на свободной доске. Указанные четыре параметра однозначно определяют пучок траекторий, Однако он может состоять из кратчайших или некратчайших траекторий на свободной от фигур доске. От этого зависит процедура его вычисления. Программа сама определяет, какой же это пучок, и выбирает процедуру его вычисления. Блок-схема этой программы показана на рис. 8.

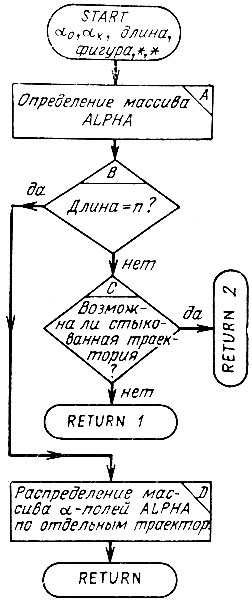
Рис. 9. Блок-схема подпрограммы получения пучка простых траекторий

Остановимся подробнее на подпрограмме получения пучка простых траекторий (рис. 9). На схеме в списке параметров указаны две звездочки, означающие возможность нестандартных выходов из этой подпрограммы RETURN 1 и 2 по адресам, которые будут стоять на Месте этих звездочек при обращении к этой подпрограмме.

В процедуре A происходит операция определения массива а-полей пучка траекторий (ALPHA). Это делается следующим образом: массив 15*15, принадлежащий фигуре, пучок которой определяется, совмещается с массивом 8*8 таким образом, что α₀-поле массива 8*8 совмещается с центральным полем массива 15*15. Результат этой операции обозначим (8*8α₀).

По сути дела происходит передача информации, записанной в массиве 15*15 -ТАВ15, массиву 8*8 - ТАВ8 по формуле

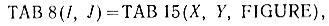
где Х = 8-X₀+I, Y = 8-Y₀+J, причем (Х₀, Y₀) - координаты α₀-поля. Аналогичная операция совершается для α_k-поля.

В результате получаются два заполненных числами массива 8*8. Складываем их как векторы, получаем новый массив 8*8. В нем определяем поля, в которых записаны числа, равные длине пучка. Список линейных координат этих полей и образует массив ALPHA.

В процедурах С и В происходит сравнение числа n, стоящего на α_k-поле массива (8*8α₀), с длиной пучка A. Если A<n или 2n_L<A, то пучок не существует (n_L - предельное число, содержащееся в массиве 15*15 для данной фигуры) и происходит выход из подпрограммы и передача управления по адресу, указанному на месте первой слева звездочки. Если же n<A≤2n_L, то возможна стыкованная траектория и снова выход из подпрограммы.

Рассмотрим, что же происходит, если длина пучка равна n. В ALPHA содержатся координаты всех а-полей траекторий пучка. Остается выяснить, как они распределяются по отдельным траекториям, т. е. получить траектории в явном виде (процедура D).

Опишем эту процедуру по индукции. Пусть к данному моменту построено N траекторий пучка, но они вычислены не до конечного α_k-поля, а лишь до (α_i-1-поля. Покажем, как вычисляются α_i-поля траектории и какие новые траектории при этом появляются.

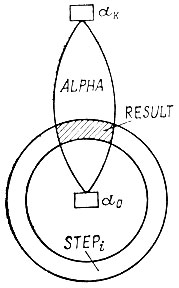
Рис. 10. Определение массива RESULT

Сначала строим массив STEP_i, состоящий из координат полей массива (8*8α₀), в которых записано число i. STEP_i - это массив полей, на которые наша фигура может попасть с α₀-поля в i передвижений, двигаясь кратчайшими путями. Далее определяем, какие из этих полей содержатся в нашем пучке, т. е. в массиве ALPHA. В результате из общих элементов массивов STEP_i и ALPHA формируется массив RESULT. Это проиллюстрировано на рис. 10. Итак, RbbULl - список координат всех α_i-полей траекторий пучка.

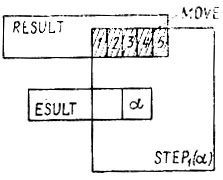
Рис. 11. Определение массива MOVE

Предположим, что у нас есть список координат всех α_i-1-полей траекторий пучка. Назовем его ESULT. Пусть α - элемент массива ESULT. Тогда определим массив STEP₁(α) координат полей, на которые наша фигура может попасть в одно передвижение с ноля а. Он определяется аналогично массиву STEP_i. Остается выяснить, какие из элементов массива STEP_i(α) содержатся в массиве RESULT. Тем самым мы найдем α_i-поля, на которые можно попасть в одно передвижение с поля α. Координаты этих полей образуют массив MOVE (рис. 11).

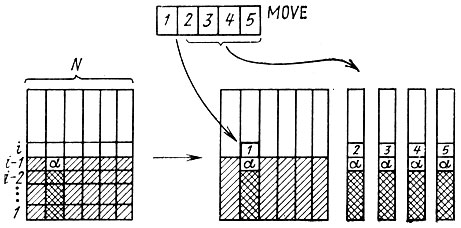
Рис. 12. Вычисление траекторий

Итак, подготовлен материал для наращивания уже имеющихся траекторий и формирования новых. Просматриваем все N уже имеющихся траекторий и ищем среди них такую, в которой α_i-1 = α. Наращиваем эту траекторию α_i = MOVE (1). Формируем новые траектории. Их число равно количеству оставшихся элементов массива MOVE. Новые траектории до α_i-поля совпадают со старой, α_i-поля в них - элементы массива MOVE (рис. 12). Эта операция повторяется для каждой старой траектории, в которой α_i-1 = α.

Описанная процедура выполнялась с элементом а массива ESULT. Теперь переходим к следующему элементу этого массива и для него повторяем процедуру. Исчерпав все элементы массива ESULT, пересылаем массив RESULT в массив ESULT. Таким образом, сделанное выше предположение о существовании массива ESULT обосновано.

N присваиваем число, равное общему количеству построенных к данному моменту траекторий. Теперь можно переходить к нахождению α_i+1-полей траекторий

Итак, в данном алгоритме вычисление всех траекторий пучка происходит не по очереди (одна траектория за другой), а параллельно.

Описание процедуры D, а вместе с ней и блок-схемы, изображенной на рис. 9, закончено. Все вышесказанное верно для любой фигуры, кроме пешки и ферзя.

Особенность пешки состоит в том, что в процедуре А для получения массива (8*8α_k) нужно использовать массив 15*15 для пешки другого цвета. Что же касается ферзя, то это единственная фигура, для которой эта подпрограмма получает не только кратчайшие траектории, а все траектории в одно и два передвижения. В памяти не хранится специальный массив 15*15 для ферзя. Если подпрограмма занимается поиском пучка траекторий ферзя, то вначале находится пучок, состоящий из траекторий, по которым ферзь передвигается, как слон. Поэтому все процедуры выполняются так, как будто ферзь - слон. Затем все начинается сначала, но находится пучок траекторий, по которым ферзь передвигается, как ладья. После этого строятся еще два пучка траекторий ферзя: "ладья+ +слон" и "слон+ладья" (траектории в два передвижения). Для этого при нахождении массива (8*8α₀) используется массив 15*15 для ладьи, а при нахождении массива (8*8α_k) - специальный массив, который отличается от массива 15*15 для слона тем, что на пустых полях последнего массива стоят двойки (в дальнейшем будем называть его массив № 7; таким образом, определены семь массивов 15*15: белой пешки, черной пешки, короля, коня, слона, ладьи и массив № 7.). Для пучка "слон+ладья" используется обратная комбинация массивов.

Полученные четыре пучка объединяются вместе и образуют пучок всех траекторий ферзя в два передвижения. Отметим, что если рассматривать отдельно траектории ферзя как ладьи или как слона из этого пучка, то они, конечно, являются кратчайшими для каждой из этих фигур.

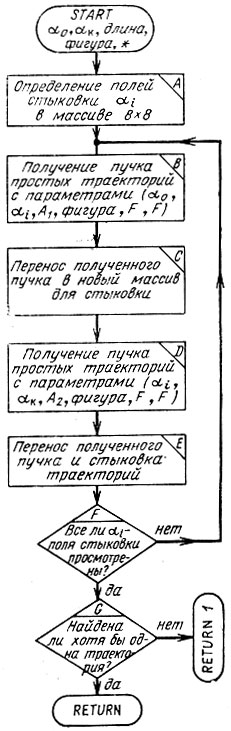
Рис. 13. Блок-схема подпрограмы получения пучка стыкованных траекторий

Вернемся к описанию блок-схемы, изображенной на рис. 8 Процедура В уже описана. Выясним, что происходит при втором нестандартном выходе из этой подпрограммы (RETURN 2) В списке параметров этой подпрограммы указано, что при таком выходе надо переходить к процедуре С получения пучка стыкованных траекторий. Блок-схема соответствующей подпрограммы изображена на рис. 13.

Список параметров здесь аналогичен списку в блок-схеме 1 рис. 9, кроме одного нестандартного выхода, который происходит, если подпрограмма не найдет ни одной траектории. Цель этой подпрограммы - поиск траекторий, составленных из двух кратчайших (на свободной от фигур доске). Следовательно, основная задача - нахождение промежуточного поля, к которому и от которого фигура движется по кратчайшим траекториям. Такие поля назовем полями стыковки. Определение этих полей происходит в процедуре А (рис. 13). Она работает так же, как процедура А на рис. 9, только получающийся в результате список координат полей называется не массивом ALPHA, а списком полей стыковки α_i в массиве 8*8.

Процедуры В и D состоят в обращении к подпрограмме получения пучка простых траекторий с различными списками входных параметров. В процедуре В вычисляется пучок с α₀-поля на салоле стыковки длиной А и в процедуре D - пучок с α_i-поля на α_k-поле длиной A₂, причем A₁ и A₂ подбираются так, чтобы A₁+А₂ равнялась длине искомого пучка стыкованных траекторий. Все нестандартные выходы из этих процедур означают переход к выполнению процедуры F, что и отмечено в списках параметров процедур В и D.

В процедуре С пучок, полученный в В, переносится в специальный новый массив для того, чтобы использовать освободившееся место для вычисления нового пучка в процедуре D. Процедура С проиллюстрирована на рис. 14,а.

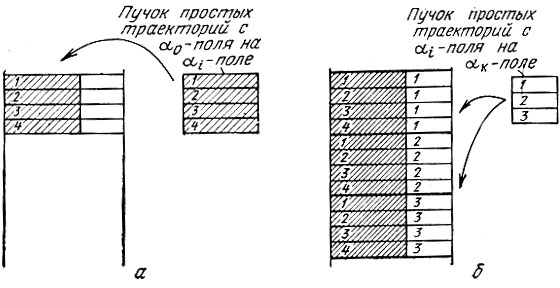
Рис. 14. Перенос пучка простых траекторий в новый массив и стыковка траекторий

После того, как получены два пучка, относящиеся к одному и тому же полю стыковки, надо произвести собственно стыковку траекторий. Если рассматривать оба пучка как два непересекающихся множества траекторий, то операция стыковки состоит в получении теоретико-множественного произведения этих множеств, т. е. нового множества, состоящего из всех пар, элементами каждой из которых являются две траектории, принадлежащие разным пучкам. Эта операция выполняется процедурой E и проиллюстрирована на рис. 14, б.

Процедуры By С, D и Е выполняются для каждого α_i-поля стыковки. Итак, блок-схема рис. 13 полностью описана.

Существуют некоторые особенности в работе этой подпрограммы для различных фигур. Нетрудно догадаться, что речь идет о пешке ферзе. Специфика содержится в единственной операции - определении полей стыковки в процедуре A.

Пешка может иметь стыкованные траектории единственного типа: траектории, содержащие превращение пешки в ферзя или другую фигуру. Очевидно, в этом случае полями стыковки могут быть лишь поля первой или последней горизонтали в зависимости от цвета пешки. Для нахождения всех полей стыковки траекторий пешки процедура А выполняется три раза, каждый раз с новым массивом 15*15, используемым для вычисления (8*8α_k). Речь идет о массивах 15*15 для коня (превращение в коня), ладьи и массиве № 1. Для нахождения массива (8*8α₀) всегда используется один и тот же массив 15*15 для пешки.

Все поля стыковки для ферзя можно определить, выполняя процедуру А три раза, каждый раз с новой комбинацией массивов 15*15 при вычислении (8*8α₀) и (8*8α_k):

1) массив 15*15 для ладьи и второй - такой же массив;

2) массив 15*15 № 7 и массив 15*15 для ладьи;

3) массив 15*15 для ладьи и массив 15*15 № 7.

Описание процедуры С блок-схемы, изображенной на рис. 8, закончено. Вход в нее может произойти только при нестандартном выходе из В. Обратимся к процедуре D.

Несмотря на то, что при вычислении пучка стыкованных траекторий мы тщательно определяли поля стыковки, при выполнении стыковки получается много траекторий, заведомо не имеющих смысла. Речь идет о траекториях, имеющих самопересечения, три а-поля подряд, лежащих на одной прямой, и т. п. Выделить и отбросить из пучка эти траектории призвана процедура D.

Процедуры F и G отражают некоторые особенности правил шахматной игры. В процедуре F к пучку траекторий ладьи или короля, найденному в предыдущих процедурах, добавляется новый пучок траекторий, первым ходом в которых является рокировка.

В процедуре G вычисляется пучок траекторий пешки," первым ходом в которых является ход на два поля. Отметим, что в этих процедурах используются подпрограммы получения пучков простых и стыкованных траекторий.

Итак, блок-схема алгоритма получения пучка траекторий с α₀-поля на α_k-поле описана полностью. Этот алгоритм является основой процедур создания зоны. Программа, работающая по этому алгоритму, получает пучки траекторий, содержащие большое количество информации, особенно, если длина траекторий превышает два передвижения на свободной доске.

Прежде чем воспользоваться этой информацией, следует решить вопрос о ее хранении. Сведения о пучках траекторий нужны на протяжении почти всей работы программы, так как от них зависит формирование зон. Какие же из этих сведений необходимо хранить? Решено хранить в памяти не самый пучок (т. е. списки полей всех траекторий), а лишь информацию о существовании этого пучка и его типе, а именно: номер фигуры, траектории которой содержатся в этом пучке, α_k-поле пучка, максимальную длину траекторий пучка, тип пучка (блокады, контроля, деблокады), а также параметры к "застыванию" этого пучка, т. е. параметры, показывающие, что в данный момент перебора движение фигуры по траекториям этого пучка не имеет смысла.

Итак, пучок характеризуется шестью параметрами. Эта информация должна быть "привязана" к полю шахматной доски, на котором стояла фигура, когда этот пучок был впервые найден, т. е. к α₀-полю. По четырем параметрам из перечисленного списка пучок однозначно восстанавливается с помощью описанной выше подпрограммы получения пучка траекторий.

Сведения о пучках можно было бы хранить в виде шестимерного массива, однако учитывая, что каждый из параметров является двузначным десятичным числом (в общем случае), линейная размерность массива составляла бы 1012, а это, конечно, неприемлемо. Поэтому мы храним информацию в виде цепного списка (рис. 15). Память, отводимая для размещения множества пучков, разбивается на "ячейки". На рисунке показаны 10 таких ячеек. Каждая ячейка предназначена для хранения шести параметров, а также адреса сцепленной с ней ячейки (указан в правом верхнем углу ячейки). Кроме того, отводим память для двух массивов 8*8, нумерация элементов в которых соответствует нумерации полей на шахматной доске.

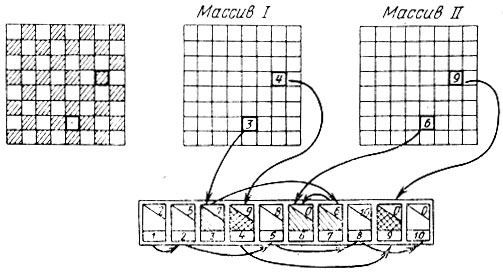
Рис. 15. Размещение множества пучков в оперативной памяти ЭВМ

Информация обо всех пучках с начальным α₀-полем "привязывается" к α₀-полям этих массивов 8*8. Это делается следующим образом: на α₀-поле массива записывается адрес ячейки, содержащей информацию о первом пучке с начальным α₀-полем, затем все ячейки с информацией о пучках, относящихся к α₀-полю, связываются в цепочку, первым звеном которой является упомянутая выше ячейка. Адрес последнего звена цепочки записывается на α₀-поле массива II. Все ячейки, в которых в данный момент не содержится информации о пучках, также связаны в цепочку.

Подобная система обеспечивает возможность стирания из некоторых ячеек информации, ставшей ненужной после того, как фигура сделает ход в игре, и использования освободившейся памяти для новой информации. Это происходит присоединением освободившихся ячеек к списку пустых.

Если в процессе перебора фигура побывает на α₀-поле, то информация обо всех пучках этой фигуры с началом на α₀-поле будет "привязана" к этому полю. Если при продолжении перебора фигура снова появится на α₀-поле (речь идет о другом варианте перебора), описанная система размещения информации даст возможность восстановить все пучки траекторий этой фигуры, связанные с этим полем и найденные в процессе предшествующего перебора. Это происходит путем последовательного просмотра цепного списка ячеек, связанного с α₀-полем, поиска нужных ячеек, считывания из них параметров пучков и применения подпрограммы получения пучков траекторий с этими параметрами.

Итак, закончено описание программ получения и хранения пучков траекторий.

Во всех рассмотренных выше программах реальная шахматная доска, заставленная фигурами, принималась в расчет лишь в том смысле, что на ней мы определяли начальное и конечное поля пучка. Сами же траектории пучка вычислялись и подвергались предварительному анализу на свободной доске. Информация о пучке, направлявшаяся на хранение, также не содержала никаких данных о заставленное траекторий пучка различными фигурами. Выход на реальную доску осуществляется лишь в момент считывания информации о пучке из памяти и расшифровки этой информации путем вычисления траекторий пучка. Каждую из этих траекторий подвергаем анализу для выяснения, в какой степени она заставлена своими или чужими фигурами. Этот анализ позволяет вычислить истинную длину траектории на реальной доске и решить вопрос о включении ее в игру. Кроме того, мы выясняем необходимость деблокады своих фигур, блокирующих эту траекторию. Анализ начинается с вычисления списка β-полей траектории. После этого проверяем, на каких β-полях стоят фигуры, превращаем их в α-поля. Отметим, что ни в одной из упомянутых выше процедур мы не вычисляли β-полей траекторий, обходясь лишь списком α-полей.

Таким образом, пучок траекторий с β-полями на реальной доске, несущий громадное количество информации, характеризуется всего лишь шестью параметрами. Это дает возможность гибко использовать ресурсы ЭВМ.