25. Черепаха и окружность
Когда мы чертили окружность с помощью процедуры ЭТО ОКРУЖНОСТЬ
ПОВТОРИ 360 [ВПЕРЕД 1 ВПРАВО 1] КОНЕЦ
кто-то из вас, наверное, снисходительно улыбнулся: Да это же правильный 360-угольник. Верно, но все же следует иметь в виду, что правильный 360-угольник - довольно хорошее приближение окружности (даже наилучшее, которое можно получить на экране). Длина этой окружности - 360 шагов. А чему равен ее радиус? Знаем, что длину окружности можно найти по формуле l=2πr. Отсюда можно вычислить и радиус:
СДЕЛАЙ "L 360 СДЕЛАЙ "Р 3.14159 СДЕЛАЙ "R :L/(2*:P) ВЫВЕДИ :R 57.2958
Следовательно, радиус равен 57.2958 шагам.
В качестве хорошего приближения окружности можно принять даже правильный 36-угольник, если только длина его стороны достаточно мала. Например:
ЭТО ОКРУЖНОСТЬ1 ПОВТОРИ 36 [ВПЕРЕД 5 ВПРАВО 10] КОНЕЦ
Мы легко можем подсчитать радиус и этой окружности. Так как ее длина в два раза меньше длины первой окружности, то и ее радиус также будет в два раза меньше, т. е. будет равен 28.6479 шагам.
Во многих случаях удобнее чертить окружности с за-данным радиусом. При вычерчивании таких окружностей черепаха поворачивается или только направо, или только налево. Вот почему мы можем чертить либо правые, либо левые окружности:
ЭТО ПРОКР :РАДИУС ПОВТОРИ 36 [ЧАСТЬПРОКР :РАДИУС] КОНЕЦ ЭТО ЛОКР :РАДИУС ПОВТОРИ 36 [ЧАСТЬЛОКР :РАДИУС] КОНЕЦ
В описании ПРОКР и ЛОКР участвуют процедуры вычерчивания одной десятой части окружности ЧАСТЬПРОКР и ЧАСТЬЛОКР. Опишем их:
ЭТО ЧАСТЬПРОКР :РАДИУС ВПРАВО 5 ВПЕРЕД :РАДИУС*3.14159/18 ВПРАВО 5 КОНЕЦ ЭТО ЧАСТЬЛОКР : РАДИ УС ВЛЕВО 5 ВПЕРЕД :РАДИУС*3.14159/18 ВЛЕВО 5 КОНЕЦ
С помощью этих процедур можно получить интересные рисунки. Начнем с программы вычерчивания пенсне:
ЭТО ПЕНСНЕ :РАЗМЕР ПРОКР :РАЗМЕР ЛПОЛУОКР :РАЗМЕР/2 ПРОКР :РАЗМЕР КОНЕЦ
Процедура ПЕНСНЕ использует процедуру вычерчивания левой полуокружности ЛПОЛУОКР, которую можно описать таким образом:
ЭТО ЛПОЛУОКР :РАДИУС ПОВТОРИ 18 [ЧАСТЬЛОКР :РАДИУС] КОНЕЦ
Теперь уже черепаха нарисует пенсне:
ПЕНСНЕ 40
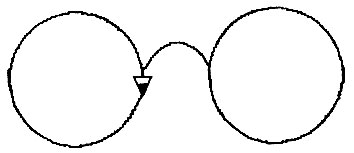
Кроме полуокружностей часто используются и произвольные дуги окружности. Дуги (правые и левые) можно чертить с помощью следующих процедур:
ЭТО ПРДУГА :РАДИУС :УГОЛ СДЕЛАЙ "N ЧАСТНОЕ :УГОЛ 10 ПОВТОРИ :N [ЧАСТЬПРОКР :РАДИУС1 СДЕЛАЙ "L ОСТАТОК :УГОЛ 10 ВПЕРЕД :РАДИУС*3.14159*:L/180 ВПРАВО :L КОНЕЦ ЭТО ЛДУГА :РАДИУС :УГОЛ СДЕЛАЙ "N ЧАСТНОЕ :УГОЛ 10 ПОВТОРИ :N [ЧАСТЬЛОКР :РАДИУС] СДЕЛАЙ "L ОСТАТОК :УГОЛ 10 ВПЕРЕД :РАДИУС*3.14159*:Ь/180 ВЛЕВО :L КОНЕЦ
В этих процедурах вам, может быть, не все ясно, но это не должно вас тревожить. Вы будете использовать их просто в качестве инструмента для вычерчивания дуг. В программировании, как и в любой другой деятельности, часто приходится использовать инструменты, не интересуясь их устройством. А теперь выполним несколько рисунков с дугами:
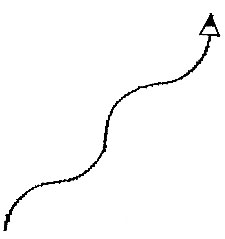
ЭТО ЗМЕЯ :РАЗМЕР ПОВТОРИ 2 [ПРДУГА :РАЗМЕР 90 ЛДУГА :РАЗМЕР 90] КОНЕЦ ЗМЕЯ 30
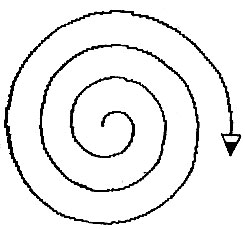
ЭТО СПИРАЛЬ :РАЗМЕР ПРДУГ А :РАЗМЕР 90 СПИРАЛЬ -.РАЗМЕР + 5 КОНЕЦ СПИРАЛЬ 6
ЭТО ВОДОРОСЛЬ : РАЗМЕР ПОВТОРИ 18 [ВОЛНА :РАЗМЕР] КОНЕЦ ЭТО ВОЛНА :РАЗМЕР ЗМЕЯ :РАЗМЕР ВПРАВО 180 ЗМЕЯ :РАЗМЕР ВПРАВО 200 КОНЕЦ ВОДРОСЛЬ 20
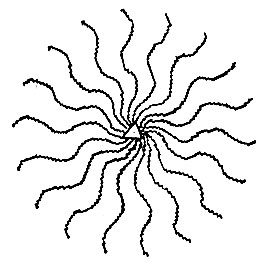
Упражнения
- Нарисуйте очки.
- Начертите окружность, описанную вокруг правильного шестиугольника со стороной 40 шагов.
- С помощью процедуры вычерчивания окружностей нарисуйте медведя. Как можно изменить программу, чтобы превратить медведя в зайца?
- Начертите 5 концентрических окружностей с радиусами соответственно 80, 60, 40, 20 и 10 шагов.
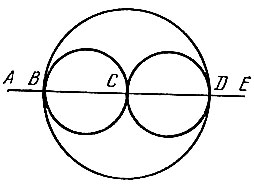
Рис. 59 - Опишите с помощью рекурсивной процедуры движение Земли вокруг Солнца.
- Начертите с помощью черепахи фигуру, представ-ленную на рис. 59.
- Пусть фигура из упр. 6 будет упрощенной схемой железнодорожной сети. Напишите процедуру, при выполнении которой черепаха будет двигаться от станции А до станции Е по разным маршрутам.
- Начертите фигуру, представленную на рис. 60.
- Начертите в круге с радиусом 70 шагов сектор в 240° (рис. 61). Сколько процентов площади всего круга занимает этот сектор?
- При помощи круговой диаграммы (см. упр. 9) представьте на экране дробь 13/18.
- В классе делали контрольную работу. Одна треть учеников решили неправильно одну задачу, одна четверть - две задачи, одна шестая - три задачи, а одна восьмая - все четыре задачи. Начертите на экране круговую диаграмму, показывающую, какая часть учеников решила все задачи.
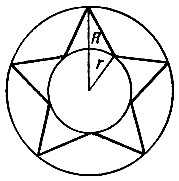
Рис. 60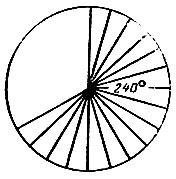
Рис. 61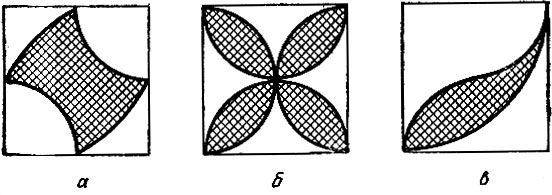
Рис. 62 - Начертите фигуры, представленные на рис. 62, и подсчитайте площади заштрихованных частей, если сторона квадрата 80 шагов.
- Напишите программу для исполнения украинской
народной песни Чорнii брови, карii очi.

|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'