Приложение 2. Теория информации

Существует несколько различных вариантов теории информации или статистической теории связи. Но теперь обычно под этим названием понимают теорию, в создании которой главную роль сыграли Шеннон [1] и Винер [2], и мы ее здесь и имеем в виду, говоря о "теории информации".

Идея, лежащая в основе теории информации, состоит в том, что количество информации может быть описано и, следовательно, измерено с помощью вероятностей или, вернее, изменения вероятностей. Можно считать, что утверждение "завтра взойдет солнце" содержит меньше информации, чем утверждение "завтра будет землетрясение", поскольку событие, о котором говорится во втором утверждении, менее вероятно, чем событие, о котором говорится в первом утверждении. Можно считать также, что количество информации, содержащееся во втором утверждении, определяется тем, насколько это высказывание меняет вероятность события.

Рассмотрим другой пример, в котором легче измерить вероятность события. Предположим, что некто бросает монету и сообщает своему другу результат. До того, как он бросил монету, его друг мог при обычных условиях приписать вероятность, не превышающую ¹/₂, каждому из сообщений "выпадет орел" и "выпадет решетка". После того как монета брошена, сообщению о том, что выпало, соответствует вероятность 1. Таким образом вероятность этого утверждения изменилась от ¹/₂ до 1, и это изменение и составляет количество информации в сообщении.

Если мы обозначим вероятность какого-либо события с точки зрения того, кто получает сообщение, через р₁ после прихода сообщения и через р₂ до его прихода и возьмем их логарифмы по основанию 2, то количество информации Н в сообщении дается формулой

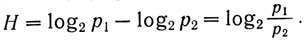
В последнем примере

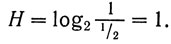
Вообще эта формула означает, что количество информации в сообщении, которое говорит о том, какой из двух равновероятных случаев имел место, т. е. которое уменьшает вдвое количество возможных исходов ситуации, равно 1. Эта единица измерения количества информации называется "бит" (binary digit).

Пусть теперь сообщение состоит в том, чтоб "выпала" какая-то одна из заранее заданного конечного числа возможностей. Или же у нас есть определенный конечный "алфавит" сигналов, и тогда можно каждому из этих сигналов приписать вероятность. Большинство сообщений будет состоять из нескольких таких сигналов, и, поскольку мы использовали логарифмы при определении информации, количества информации, заключенной в сигналах, выбранных, чтобы составить сообщение, можно сложить, чтобы получить информацию, которую несет все сообщение.

Если все буквы равновероятны, то количество информации, заключающееся в одной букве, определяется по правилу:

Число битов = log₂ (число букв в алфавите).

Например, если в алфавите 8 букв, то по этому правилу при условии, что кодирование было предельно экономным, каждая буква несет 3 бита информации. Можно сказать иначе: если бы каждую букву нужно было закодировать двоичными символами 0 и 1, то потребовалось бы три таких символа. Почему это так и как это можно конкретно сделать, видно из следующей таблицы;

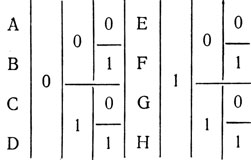
(Например, А = 000, В = 001 и т. д.)

В случае если буквы не равновероятны, тоже можно получить выражение для количества информации, приходящегося в среднем на одну букву, пользуясь формулой

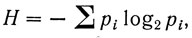
где p_i - вероятность i-й буквы.

Эта величина называется по аналогии со статистической механикой энтропией.

Мы считали в примере с бросанием монеты, что р₁ равно единице. Но это, очевидно, не обязательно, и в теории связи ситуация рассматривается в общем виде, как показано на рисунке:

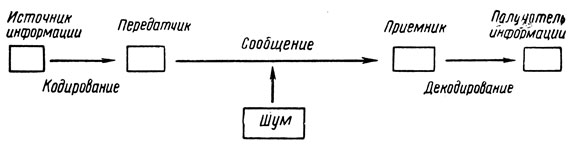
Здесь из-за присутствия шума, т. е. постороннего влияния, оказываемого на сигналы во время передачи, вероятность того, что принимаемое сообщение верно, уменьшается от 1 до некоторой меньшей величины. Один способ справиться с шумом и уменьшить вызываемую им ошибку может состоять в том, чтобы повторять каждый сигнал: чтобы закодировать букву В в последнем примере, мы могли бы взять последовательность 00, 00, 11 вместо 0, 0, 1. Тогда при той же скорости передачи сигналов скорость передачи информации уменьшится вдвое.

Информация дополнительных двоичных разрядов называется "избыточной", и избыточность можно вообще рассматривать как меру экономности передачи. Избыточность принимается равной числу

выраженному в процентах. В случае, только что описанном, где для передачи наших 8 букв мы теперь расходуем 6 битов вместо 3 на каждую букву, избыточность составляет 50%.

Шеннон показал, что, пользуясь избыточностью при передачах по каналу с шумом, можно в принципе передать любое сообщение сколь угодно надежно. Максимальная возможная скорость передачи информации по данному каналу с шумом называется его "пропускной способностью".

Область явлений, к которым применимы намеченные здесь понятия, конечно, не ограничена рамками латинского алфавита. Сюда входит любая система связи, располагающая конечным числом различных типов сигналов или символов. Вообще подходит любая ситуация, в которой может произойти конечное множество событий, каждому из которых может быть приписана вероятность

Из всего этого, однако, следует, что изменение информации не имеет смысла до тех пор, пока не указано, какой при этом выбран "алфавит". Утверждение о том, что некий сонет Шекспира содержит определенное количество информации, не имеет смысла до тех пор, пока не сказано, что принято за алфавит - обычный английский алфавит, или совокупность слов английского языка, или совокупность строчек во всех сонетах Шекспира, или совокупность всех возможных распределений типографской краски на странице и так далее, И ясно, что количество информации будет различным во всех этих случаях.

В связи с этим стоит подчеркнуть, что, поскольку теория информации имеет дело только с относительными вероятностями символов и сигналов и тому подобными "событиями", она ничего не говорит о содержании информации, передаваемой в сообщении. Следовательно, сонет Шекспира и бессмысленный набор букв содержат одинаковое количество информации, если за алфавит принят оброчный английский алфавит: вероятности появления каждой буквы в обоих случаях одинаковы и оба "сообщения" имеют одинаковую длину. Этот факт очевиден, но при определенных условиях легко забывается, что часто приводит к переоценке возможностей теории информации в строго шенноновском смысле. (Предприняты некоторые поиски, например, в работе Макки [3] мер информации, которые бы учитывали "смысл"; но здесь мы не будем их обсуждать.)