День 7. Оптимальное проектирование (Как сделать конструкцию подешевле? Где расположить торговый центр?)

 Айдым... починила всю ветхую одежду на 
народе в тех местах, где видно было тело; 
на многих людях ей пришлось укоротить одежду, 
чтобы выиграть материал и пришить его тем, 
у кого не хватало. 

А. Платонов "Джан" Лучшее - враг хорошего (Народная пословица)

Этому итальянцу чудились подчас странные вещи. Ему казалось, что солнце находится в середине системы планет. Это будоражило умы его противников и сторонников, а так как первые были куда сильнее вторых, он едва не поплатился жизнью. Другие его мысли, быть может, не так сильно потрясали сознание, но и они, обращаясь затем в строгие системы уравнений, стали живыми родниками для многих областей техники. Ну взять хотя бы такое простое наблюдение. Глядя на консольную балку с камнем, подвешенным на конец (рис. 26), Галилео Галилей пришел к выводу, что часть материала в ней лишняя, иначе говоря, если отбросить не заштрихованную часть материала, то получившаяся балка криволинейного очертания выдержит камень того же веса, что и балка в виде прямоугольного бруса, но материала на нее пойдет в 1,5 раза меньше.

Если перевести рассуждения Галилея на строгий язык современной техники, можно сказать, что прямоугольный брус -это допустимое решение задачи проектирования конструкции, которая призвана поддерживать упомянутый груз, а искривленная балка У-оптимальное решение той же задачи. Здесь уже не только решается задача проектирования, то есть находится форма бал|;и, которая способна выдержать камень, но одновременно проявляется забота об экономии материала для нее. А с точки зрения кибернетики - это оптимальное управление высотой сечения балки.

Отметим, что управление параметрами проекта обычно велось в программном режиме. Лишь в последнее время появились предложения о переходе и в этом виде управления на более гибкий следящий режим.

Классические математические методы позволяли решать лишь простейшие задачи оптимального проектирования и оказывались непригодными при попытке решить задачи реальные.

Применение методов математического программирования в оптимальном проектировании, которое началось в пятидесятых годах, дало резкий качественный скачок в решении проблемы поиска оптимальных инженерных решений. "Там, где инженерная мысль пробиралась ощупью, вслепую, цепляясь за шаткий фундамент интуиции, натыкаясь на рифы подспудных предубеждений, слепо доверялась опыту и не замечала, как он из союзника превращался в противника, математическое программирование уверенно прочерчивало трассу. Поясним это несколькими примерами.

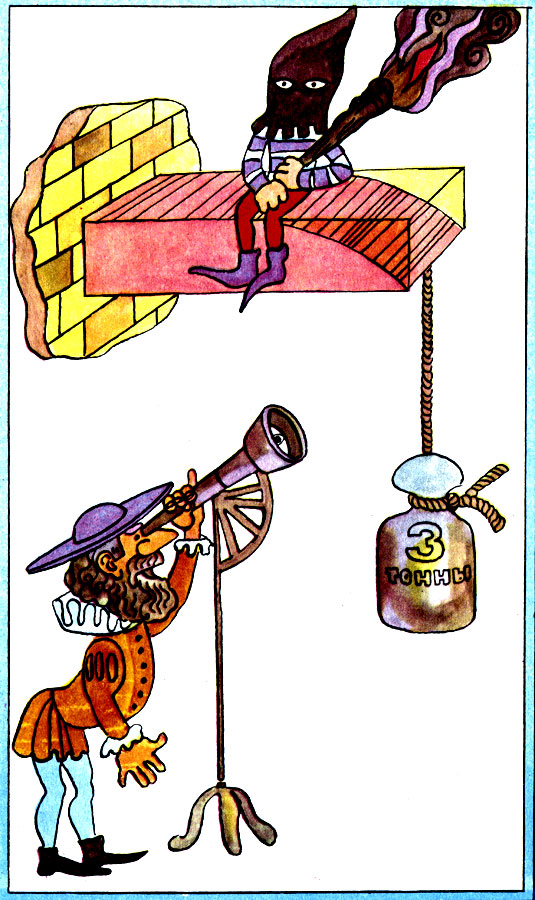
Рис. 26

Проектируется сечение железобетонной плиты, которая состоит из бетона и стали. Такую плиту вы почти наверняка увидите у себя над головой, если живете в новом доме. Ясно, что чем больше заложить бетона, тем меньше понадобится стали. Но сколько нужно того и другого, чтобы стоимость плиты была минимальной? На рис. 27 слева представлено решение этой задачи, которое получил опытный проектировщик на основе своей интуиции и опыта. Справа решение, которое выдала электронная вычислительная машина с помощью математического программирования. Машине показалсь, что высоту сечения нужно уменьшить на 2 см, соответственно несколько увеличив расход стали, и плита стала дешевле на 6%.

Предвидеть это проектировщик не мог: ведь за этими цифрами скрывается долгий утомительный расчет. А интуиция инженера предохранит его от ошибки на 20 см, но ошибка на 2 см проскользнет мимо нее незамеченной.

Или другой пример. Требуется заложить стальные стержни в железобетонную квадратную плиту (рис. 28). Можно, конечно, положить сетку с ячейками постоянного размера, и в некотором смысле (с точки зрения технологии изготовления) это проще всего (левый рисунок). Но инженеру интуитивно ясно, что стальные стержни нужнее всего в центре плиты, где больше избигающие моменты. Поэтому возникли и вошли в практику схемы расположения стальных стержней, показанные на среднем рисунке. А схему справа выдала электронная машина с помощью метода математического программирования.

Вторая схема экономит, по сравнению с первой наиболее прямолинейной, 25% стали, но она продукт человеческой интуиции и потому несовершенна. Не удивительно, что третья схема экономит 10% стали по сравнению со второй, а выдерживают все три плиты одну и ту же нагрузку.

Обратите внимание, что человеческая интуиция способна ухватить тенденцию, но не может предсказать некоторых важных деталей, из которых и сложились эти 10%.

Случайно ли, что для более сложной конструкции экономия, полученная с помощью электронной машины, оказалась больше? Нет, это общее свойство всех систем. Чем система сложнее, тем беднее по отношению к ней возможности человеческой интуиции. Для балки Галилея опытный проектировщик по интуиции без труда найдет решение, отличающееся от оптимального лишь на 2-3%.

Интересно, что если в рассмотренной задаче о плите просто перебирать "в лоб" все варианты, то и машина, и человек одинаково бессильны: ведь понадобилось бы перебрать примерно 10^-15 вариантов.

Рис. 27

А вот пример из другой области техники - проектирования энергетических сетей. На электронной машине находили сеть наименьшей длины, связывающую между собой 20-30 заданных точек^*. После этого задачу поручали нескольким опытным проектировщикам. Их решения оказывались различными, но в средней на 10% хуже, чем у машины, то есть проектировщики предлагали сети на 10% длиннее.

^* (Не путайте с задачей об оптимальном маршруте: сеть должна пройти через все точки.)

Тут содержится ответ на такой не праздный вопрос: а может быть, человеческая интуиция достаточно надежный инструмент для принятия проектных решений? И та оптимизация, которой мы добиваемся, потонет в стоимости затраченного машинного времени? Это не так. Приведенные примеры сравнения машинного и "ручного" проектирования не случайны, они отражают объективный предел возможностей интуиции человека по предсказанию поведения сложных систем. Психологам еще предстоит обосновать этот факт с позиций законов деятельности человеческого мозга, но принципиально он уже установлен: при попытке назначить оптимальные параметры достаточно сложной системы специалист обычно уклоняется от оптимального решения по критерию стоимости примерно на 10%; причем безразлично, идет речь о назначении параметров многоэтажного здания, о расстановке станков в цехе, о проектировании электрической сети или автоматического прибора, распределении ресурсов в календарном планировании и т. д. По-видимому, здесь мы имеем дело с некоторой биологической константой, зависящей, конечно, от личности человека, но все-таки лежащей в ограниченном диапазоне.

Значит ли все это, что машина уже совершеннее человека в принятии проектных решений? Пока нет. Принципиальные, главные решения - например, перекрывать здания балками или фермами, какую строить плотину, принимает человек. Но вот идеально подогнать детали, исчерпать или, как говорят проектировщики, "вылизать" все скрытые резервы человек не в состоянии, тут машина идет впереди. И здесь мы подходим к очень важному пункту: всякий раз, когда сравниваются различные технические решения, они должны быть представлены своими оптимальными вариантами. В противном случае легко прийти к неверным выводам. Скажем, сравнивая лучшую в мире телегу с худшим автомобилем, нетрудно убедиться в преимуществах гужевого транспорта. А не на таких ли основаниях браковались некоторые прогрессивные типы конструкций? Таким образом, роль оптимального проектирования не ограничивается достижением сиюминутной экономической выгоды; оно необходимо и для определения путей технического прогресса.

Чтобы получить хотя бы беглое представление о сущности методов оптимального проектирования, перенесемся снова в кабинет Павла Ивановича.

...Ни сверкающий зимний день, ни новые обои в кабинете, ни успехи любимой хоккейной команды не улучшали его скверного настроения. Даже милое создание в мини-юбке не вывело его из мрачной сосредоточенности, когда оно проскользнуло мимо секретарши и подсело к столу на краешек кресла. "Горит план по новой технике, наверняка будет перерасход материалов и фонда заработной платы, не хватает рабочих" - такие тяжкие мысли бродили в уже немолодых мозгах Павла Ивановича.

Рис. 28

- Ну что там у вас? - безнадежно спросил он у создания. Куда больше порадовали бы его взор десяток молодцов-бетонщиков, приди они наниматься на работу. - Вы что, устраиваться на работу?

- Я уже шесть дней работаю у вас и хочу уйти.

- "Работает? Что-то не припомню?" - рассеянно подумал Павел Иванович, принимая протянутое заявление.

Управляющему стройтрестом № 6 тов.

П. И. Фиалкову

математика Скобкиной

Ирины Михайловны

Заявление

Прошу освободить меня от занимаемой должности, так как никакой работы по специальности мне не дают.

И. Скобкина

- Так! - выдохнул Павел Иванович, с трудом вспомнив, что в его обширном штате где-то с недавних пор действительно числился математик. -Уходить решила?

Он постарался изобразить сожаление. На самом деле никакого сожаления не было, просто не хотелось, чтобы число прегрешений треста дополнилось разбазариванием молодых специалистов (за это уже однажды попало).

- А что не нравится? Работа тяжелая? - Павел Иванович читал газеты и меньше всего хотел бы прослыть гонителем математики или тем более входящей в моду кибернетики.

- Вообще никакой работы! - Ирочка сверкнула подкрашенными глазками. - Если хотите, это тяжело, особенно сразу после шести экзаменов в сессию.

- Математика - это дело хорошее. Помню учил когда-то интегралы и дифференциалы... Но скажу вам честно: двадцать лет уж, как руковожу трестом - ни разу они мне не понадобились.

- Математика - это не только дифференциалы и интегралы, - вспыхнула Ирочка.

- Ну да-да, конечно, - примирительно буркнул Павел Иванович, хотя, честно говоря, ничего кроме дифференциалов и интегралов вспомнить не смог, да и то вспомнил лишь, что один из них (интеграл?) бесконечно малая величина, но решил от позора подальше, эрудицией не щеголять. А вместо этого: - Понимаете, дорогая Ирина... э-э...

- Михайловна.

- Да, Михайловна, сейчас конец года, сотни более важных проблем. Да-да, заходите Игнатий Евстафьевич, - бросил он заглянувшему начальнику технического отдела, - я сейчас освобожусь. Так вот, я вам обещаю, как только год кончится, мы и начнем. Обучите нас снова интегральному исчислению, применим его к управлению производством или там еще к чему-нибудь. А сейчас, мне, поверьте, не до этого. План годовой горит, рабочих нет, механизмов не хватает - только математики не доставало!

- А вы не думали, что современная математика поможет решить ваши проблемы?

- Э, сразу видно, что не знаете вы суровой прозы жизни. Тут совсем иные средства нужны. Вот, видите, сидит Игнатий Евстафьевич. Думаете, он меня утешить пришел? Ничего подобного! Наверняка новая проблема. Так ведь?

- Точно, Павел Иванович, проблема, хотя и небольшая. Мороз сейчас, бетонировать нельзя на площадке, а на заводе сборного железобетона цех стал на ремонт, знаете. Вот пришлось заменить железобетонные не разрезные прогоны на стальные, двутавровые. Ну, расчет, подбор сечений мы у себя прикинули; так что вам только подписать вот тут^*.

^* (Дотошный читатель может здесь заметить, что управляющий трестом такими вопросами обычно не занимается. Но не вводить же нам только ради этого эпизода в число персонажей книги еще и главного инженера! Будем считать, что он в командировке в Усть-Илиме. )

- Вот тут, вот тут! - взорвался Павел Иванович. - А что это значит. Вы понимаете? Это значит - новый перерасход металла, вот что. Ну, товарищ математик, говорите, как вы нам тут поможете? Мороз ликвидируете методом этого... Эйлера? Или проинтегрируете снабженцев, и они вам из пятого измерения прокат достанут?

- Покажите мне чертеж балки, Игнатий Евстафьевич, - сказала Ира. - Ага, ясно. Вы знаете, доставить прокат из пятого измерения я пока еще не умею, морозом управлять тоже, но все-таки я у вас до завтра заберу заявление; кажется, что-то сделать можно.

- Выдумаете? -заволновался Игнатий Евстафьевич, протирая очки. - А я не уверен, балку запроектировал опытный расчетчик, и с нею все в порядке. И мы можем далеко зайти, если позволим всяким без году неделю...

Дотошный читатель может здесь заметить ,что управляющий трестом такими вопросами обычно не занимается. Но не вводить же нам только ради этого эпизода в число персонажей книги еще и главного инженера! Будем считать, что он в командировке в Усть-Илиме.

- Постойте, - прервал его Павел Иванович.- Давайте завтра в 17.00 собиремся и выслушаем Ирину Михайловну. А вдруг действительно поможет, хотя, убей меня, не пойму как.

- Но ведь, Павел Иванович, - начал было Игнатий Евстафьевич.

- Завтра в 17.00! - Павел Иванович умел быть твердым в своих решениях.

-"Ладно, подожду с заявлением до завтра", - подумала Ира, уходя в этот день из треста. Тонкий, невесомый рулончик кальки был у нее в руках; он внушал неопределенные надежды.

...К пяти часам Павел Иванович вместе с Ирой уже сидел у стола и недоверчиво вглядывался в листки с цифрами.

- Можете считать, что я достала для вас 4,2 тонны стали.

- Как, каким образом? Мы приняли сечения в притирку по расчету. У вас ошибка, - вскипятился Игнатий Евстафьевич.

- Для этого мне пришлось использовать программу для вычислительной машины. Нет, нет, не пугайтесь! Я не буду объяснять ее вам. Я просто покажу на простом примере, как она работает. Вот схема вашей балки с нагрузками (рис. 29). Вы подо-брали такие сечения (см. рис. 29). Они, конечно, годятся, то есть выдержат нагрузку...

- Еще бы, -процедил Игнатий Евстафьевич.

- Но весят они - посмотрим по сортаменту:

А теперь зададим вопрос: нельзя ли нести ту же нагрузку с помощью меньшего веса? Оказывается, можно. Вот как должна выглядеть оптимальная балка (см. рис. 29).

- Ее вес 456,3 кг. Выходит, я сэкономила вам (491,2 - 456,3)120 = 4,2 т прокатной стали - ведь всего балок 120^*.

^* (Это решение Ира получила с помощью динамического программирования. Первоначально в рукописи был подробный расчет, однако им прошлось пожертвовать в целях экономии места. Впрочем, читатель может удовлетворить свою любознательность, обратившись к библиографии [ 3 ])

Рис. 29

В тот день Иру уговорили подождать с уходом. Хотя бы до завтра...

Оптимальное проектирование несущих конструкций - это область строительного проектирования, более всего разработанная, но не единственная и не самая важная: ведь несущие конструкции составляют не больше 20% стоимости коробки здания и значительно дешевле стенового ограждения. Но имеются модели задач оптимизации зданий, в которых учитывается минимум суммарной стоимости несущих и ограждающих конструкций. Например, повышение высоты сечений несущих конструкций приведет при заданном внутреннем свободном габарите помещений к увеличению стоимости стенового ограждения, хотя стоимость собственно каркаса при этом уменьшится. Таким образом, при назначении высоты сечений несущих конструкций можно учитывать возрастающую стоимость ограждения.

Другой важный класс задач составляют задачи оптимизации водопроводных сетей, теплофикационных и вентиляционных систем и других видов инженерного оборудования зданий. Наилучшим методом для решения этих задач снова оказалось математическое программирование. К сожалению, уровень разработки этих проблем пока еще отстает от разработок задач оптимизации конструкций.

По мере ухода от частных локальных задач и перехода к оптимизации целых систем становится все труднее выбрать критерий оптимальности. Для отдельных конструктивных и инженерных элементов часто является достаточным критерий минимума расхода материалов или близкий к нему критерий минимума стоимости. Однако в задачах более общего плана этот критерий становится уже непригодным.

С особой остротой это проявилось в тех случаях, когда делались попытки решать архитектурные или градостроительные задачи, не связанные с конструкциями или инженерной стороной дела.

Иногда в таких задачах удается выделить и оценить количественно основное качество системы, то, чего мы хотели бы добиться. Но чаще всего сделать это весьма непросто.

Обсудим эти трудности на примере одной такой задачи.

...Стоит за горами, за долами молодой город Приреченск, который задан нам в виде точек расселения людей. В этом городе нужно расположить торговый центр с тем, чтобы он принес жителям города максимум удобств. Где его расположить? (рис. 30). Первое, что приходит в голову, расположить центр там, где достигается минимум суммарного расстояния от центра до каждой точки города. Расстояние от i-й точки расселения до центра обслуживания с неизвестными пока координатами а и b выразится, по теореме Пифагора как

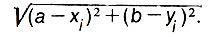
Сумма всех этих расстояний даст целевую функцию

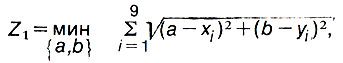
а минимум этой целевой функции и даст наилучшее расположение центра. Как только жители Приреченска узнали об этой затее (а народ там жил грамотный, одних кандидатов наук было в семьсот двадцать раз больше, чем в Москве в XVI веке), в редакцию местной газеты "Приреченская правда" поступил ряд писем от читателей.

"Я живу в микрорайоне № 3, - писала пенсионерка Патрикеева. - У нас тут три тысячи жителей. А в микрорайоне №8 - всего одна. Почему же мы должны гонять свои "Жигули" на целый километр дальше? Это несправедливо. Предлагаю целевую функцию, которая учитывала бы количество жителей в каждом микрорайоне ff, то есть чтобы минимизировалась сумма взвешенных расстояний:

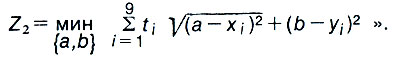
"Это не по-честному, - откликнулся в следующем номере пенсионер Правдолюбов. - Не для того мы боролись, чтобы каждый из пятисот жителей нашего микрорайона № 7 тащился в микрорайон № 3 за сырокопченой колбасой или апельсинами из Марокко. Нужно думать об интересах граждан, которые оказались в самом худшем положении, а не прятаться за благополучные средние показатели. Вот целевая функция, которую я предлагаю:

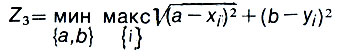
Может, средний показатель будет и похуже, зато никто не будет сильно, обижен. Общественное счастье не может строиться на несчастье хотя бы немногих..." - дальше шли цитаты из Ф. М. Достоевского, далекие от нашей тематики.

"Насчет общественного несчастья, тов. Правдолюбов, - писал старшина в отставке Прикладов, - это так точно. Но разрешите доложить, что так можно дойти до полного абсурда. Разъясняю задачу: есть в нашем городе микрорайон № 9, в котором сосредоточены жители силами до пятидесяти человек. Выходит, их интересы составляют не меньше, чем у района № 3 (три тысячи сабель)? В соответствии считаю необходимым дислоцировать торговый центр по целевой функции

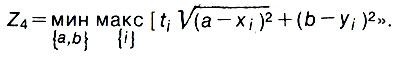
Рис. 30

"Я конечно, женщина малограмотная и писем в газету никогда не писала, но после того как правнук объяснил мне теорему тов. Пифагора, решила встренуть в ваш спор. Это что же это получается, а? Что же вы расстояния-то по прямой меряете? Ведь ходить-то будете по улицам, которые в нашем городе чаще всего параллельны осям х и у. Поэтому правнук, отправляясь вступать в пионеры, наказал мне послать вам такую целевую функцию:

Пра. Бабушкина

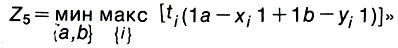
"Смотрю я на вас, товарищи, и думаю: эх! Да, не научили вас деньги народные считать. Ведь если воспользоваться критерием № 5, то придется сломать гордость нашего города - новый кинотеатр "Приречье", а если критерий № 4 - одноименный ресторан. Нам нужен самый дешевый торговый центр, а его мы получим только на пустом месте, чуть восточнее микрорайона № 9. Между прочим, для интересующихся, я живу в микрорайоне № 1.

Депонентов, бухгалтер-пенсионер^*".

^* (Авторы, как и наш проницательный читатель, тоже заметили, что все письма в редакцию принадлежат в нашем примере пенсионерам, но что делать, такова жизнь.)

Строго теоретически эта дискуссия могла длиться бесконечно: ряд возможных критериев оптимальности ничем не ограничен. И ориентироваться в них непросто. Для этого недавно создана целая наука - квалиметрия, то есть наука по измерению качества. Главный инструмент этой науки - метод экспертных оценок. Метод этот всем хорошо известен: именно с его помощью определяют чемпионов по гимнастике и фигурному катанию, где результаты не выразишь в метрах и секундах. Для оценки проекта эксперты назначают вес каждого критерия в виде числа от 0 до 1, а затем эти веса усредняются.

Как хорошо знают любители спорта, в легкой атлетике и футболе результаты соревнований куда объективнее тех, что доставляет метод экспертных оценок, скажем, в гимнастике. К тому же условия работы экспертов по оценке проектных решений сложнее, чем в спорте, где многое ясно даже дилетанту. Поэтому оптимальные проектные решения, полученные на основе экспертных оценок, нуждаются в трезвом подходе. Но и другая крайность - полное отрицание экспертных оценок - недопустима: каждый строгий метод оптимизации с одним критерием - это сильно вырожденный метод экспертных оценок, где экспертный коллектив состоит из одного человека, автора метода, который одному критерию присваивает вес 1, а остальным - 0.

Кстати, метод экспертных оценок - яркий пример того, что новое - это прочно забытое старое. Недаром его иногда называют еще дельфийским методом. Почему "дельфийским"? А вот почему.

Допустим, что проблема, где строить торговый центр, возникла не сейчас, а этак тысячи две лет назад. В те времена бывалые люди непременно посоветовали бы главному архитектору Приреченска обратиться в храм Аполлона в греческом городе Дельфы. При этом храме действовал экспертный коллектив жрецов под названием оракул. За немалую мзду жрецы храма передали бы его вопрос главной жрице храма. Жрица сидела на треножнике у расщелины скалы, из которой выходили ядовитые газы, и одурманенная ими, что-то несвязно выкрикивала. Посторонние в это помещение храма не допускались (точь в точь - сегодняшне вычислительные центры). А жрецы истолковывали этот бред, перемалывая его в полезные советы. И, по- видимому, истолковывали здраво; иначе эта "экспертная фирма" не просуществовала бы полторы тысячи лет, невзирая на теснившее ее христианство. Клиентов фирмы подкупало то, что не требовалось четкой формулировки задачи и тематика вопросов к оракулу не ограничивалась ничем. Конечно, жрица с ее невнятицей, которая якобы общалась лично с самим Аполлоном, и выражала его мнение, была чисто декоративным элементом, а все решали жрецы. Они выдавали ответ в письменной форме, одно время даже в стихах, и скрепляли его подписями.

Но здесь мы сойдем с пути губительных аналогий и закончим обсуждение темы оптимального проектирования, пригласив читателя в следующий день.