Анализ изображений

Непросто выбрать такую область, которая была бы, с одной стороны, не слишком трудной, а с другой - достаточно богатой, чтобы многому можно было научиться. Для первых исследований по машинному зрению мир кубиков представлялся идеальным, точно так же как и для исследований по естественному языку. Действительно, проблема описания предметов достаточно проста: все возможности исчерпываются ортогональными проекциями треугольников, квадратов и других простых плоских фигур. Основная подцель поэтому представлялась как исследование вопросов решения задач, о которых сейчас нам достаточно много известно, а создание машинного зрительного восприятия, по крайней мере для мира кубиков, должно было стать содержанием летнего научного проекта. Сегодня такой оптимизм выглядит достаточно глупо. Сегодня мы знаем, что задачи эти трудны и что равную важность имеет понимание вопросов обработки изображений, использование ограничений и представление знаний даже в таком простом мире, как мир кубиков.

Мир кубиков изучался уже долго

Многое удалось выяснить в ходе построения систем для копирования построек из кубиков, подобных изображенным на рис. 8.2. Эта задача была решена для достаточно общих структур из блоков Уинстоном, Хорном, Бинфордом и Фрейдером с использованием двух частей: устройства понимания изображений, которое создает контурный рисунок, и устройства понимания сцены, которое использует этот рисунок. Система выглядит как слоеный пирог, в котором анализ изображений и анализ сцен переложен изображением, контурным рисунком и трехмерным описанием.

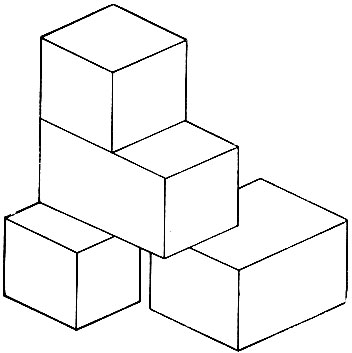
Рис. 8.2. Конфигурация блоков, скопированная роботом Уинстона, Хорна, Бинфорда и Фрейдера в декабре 1970 г.

В таких системах части, связанные с изображением и сценой, действуют совершенно независимо, поскольку единственная связь между ними осуществляется через рисунок. Достаточно рано на примере этой системы стало ясно, что наверх должна поступать не только информация о положении узлов и соединениях.

На этом пути возникает две возможности. Одна из них состоит в склеивании двух уровней обработки, тогда как другая состоит в улучшении промежуточной базы данных, пока представляющей собой контурный рисунок, т. е. весьма узкий канал, через который мало что может быть передано. Эта альтернативная возможность приводит к выделению описания и к превращению плоского контурного рисунка в некоторое богатое описание, получившее название первичного наброска. В соответствии с одной точкой зрения знания, связанные с разумным решением задач, проникают даже в исходные функции обработки изображения, изменяя их поведение на основе частичного знания. В соответствии с другой - решение задач на уровне изображений гораздо менее полезно, чем это предполагалось ранее. По-видимому, обе точки зрения справедливы. Обеим будет уделено внимание ниже.

Направляемое знанием прослеживание приводит к построению рисунков в мире кубиков

Рис. 8.3 иллюстрирует работу лучшей программы, созданной Сираи, которая выделяет линии. Сначала она находит резко очерченную границу фона. После чего основная процедура прослеживания движется вдоль подозреваемых линий, используя для этого модуль анализа профиля. Как видно из рис. 8.4, в качестве корректирующей обратной связи выступает дрейф, отмеченный в ходе профильного анализа.

Чтобы начать работу устройства прослеживания, Сираи применяет эвристические сведения. Иногда это - представление о том, что в мире блоков имеется тенденция к появлению параллельных линий, иногда о том, куда смотреть, если линия теряется. В некоторых случаях специалист по контексту поставляет информацию о том, в каком направлении делать пробу при выходе из узлов. Благодаря этим знаниям удается вывести и проверить достоверность местоположения неясных линий, используя элементы, которые в противном случае оказались бы неэффективными.

Как ни высока эффективность программы Сираи, все еще не ясно, следует ли привносить знания высшего уровня в анализ изображений в более общей ситуации. Мир кубиков может здесь дать ложное представление именно потому, что в нем оказывается возможным этот гигантский скачок от точек изображения к трехмерной модели. Весьма вероятно, что для вычислительных машин, взаимодействующих с реальным миром, требуется значительное усиление в промежуточных слоях пирога.

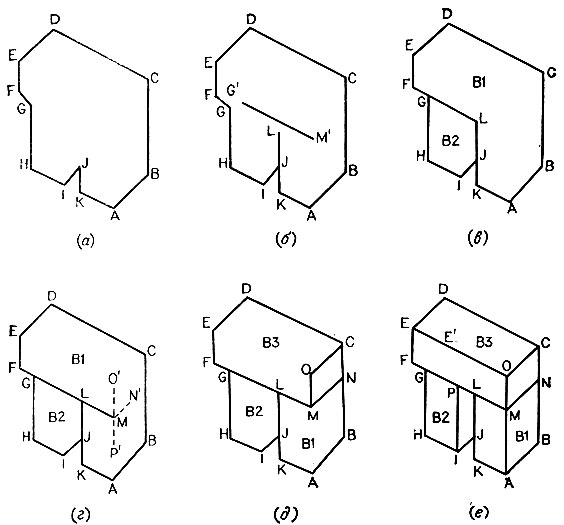
Рис. 8.3. Гетерархическая система машинного зрения Сираи начинает анализ с поиска ярко выраженных граничных линий. Более трудные внутренние линии отыскиваются с помощью процедур, использующих знания об изображениях предметов в мире блоков при прослеживании стандартных профилей интенсивности. (Из книги под ред. П. Уинстона 'Психология машинного зрения'.- М.: Мир, 1978 г.)

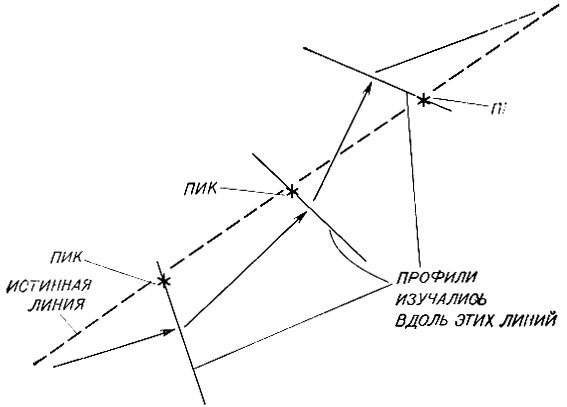
Рис. 8.4. Прослеживание линии. Исследуются профили, перпендикулярные направлению прослеживания. Наблюдаемые максимумы на этих профилях дают необходимую обратную связь для коррекции направления прослеживания

Фильтрация необходима даже при исследовании профилей интенсивности в мире кубиков

Экспериментально те линии, которые должны появиться на контурном рисунке сцены из блоков, соответствуют изменениям интенсивности, показанным на рис. 8.5, или некоторой их комбинации. Ступенька - это подъем или спад интенсивности. Такое изменение может быть резким или же постепенным. Крыша - это изменение скорости изменения интенсивности. Пик - это узкий выброс.

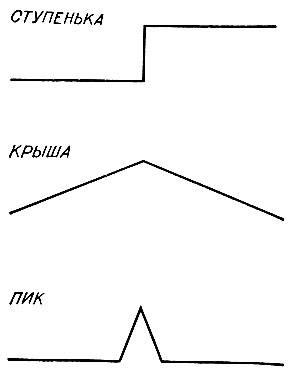
Рис. 8.5. Стандартные профили интенсивности. Резкие выпуклые края должны порождать резкие ступеньки, однако обычно возникают ступеньки сглаженные. Вогнутые края порождают 'крыши', потому что встречающиеся поверхности подсвечивают друг друга. Зеркальные отражения приводят к резким максимумам - 'пикам', которые на практике часто комбинируются с профилями других типов

В идеальном мире кубиков эти характерные профили можно наблюдать непосредственно, но на практике различные помехи заставляют использовать фильтрацию, задачей которой является выявление исходных изменений и подавление наложенных.

• Устройства ввода не дают простых ясных изображений. Следует учитывать различную чувствительность прибора в различных участках изображения, ошибки в определении координат точек изображения, электронный шум, нестабильность источников света и невозможность улавливания слишком большого разнообразия величин интенсивности.
• Даже сцены из мира кубиков создают сложные изображения, представляющие трудности для программ из-за эффекта взаимной подсветки, ложных царапин, отпечатков пальцев и пыли. Нельзя заниматься миром кубиков, используя прямолинейные подходы.

Одна популярная операция фильтрации состоит в вычислении новых величин по старым путем сложения нескольких точек справа и вычитания нескольких слева. Этим объединяются усреднение и обнаружение наклонов. На рис. 8.6 показано, что получится, когда такой фильтр применяется к стандартным профилям. Заметьте, что кривые заметно отличаются друг от друга. Их легче обнаружить в присутствии шумов, чем породившие их необработанные профили, благодаря этому объединенному эффекту усреднения и обнаружения наклона. Используя фильтрованные профили, система прослеживания Сираи обнаруживала и локализовывала ступенчатые края, применяя алгоритм, который иллюстрируется на рис. 8.7 и определяется следующим образом:

• Предполагая, что интенсивность после фильтрации дается функцией F(x), найти положение х = х_макс, где F(x) максимальна. При прослеживании линии эта фильтрация производится лишь на небольшом расстоянии по обе стороны от траектории прослеживания.
• Убедиться, что F(x_макс)>T_мин, где Т_мин - значение порога, устанавливающего минимальную высоту пиков.
• Найти точки слева и справа от х_макс, где F(x) минимальна. Пусть это будут точки х_{лев-мин} и х_{прав-мин}.
• Сначала убедиться, что F(x_макс)-F(x_мин)>T_разн, затем, что F(х_макс) - Т(х_{прав-мин})>Т_разн>. Пик должен значительно возвышаться над окружающими точками.
• Найти крутые склоны с каждой стороны от максимума, там, где интенсивность после фильтрации достигает примерно 3/4 максимального значения. Пусть точки х_{лев-плечо} и х_{прав-плечо} соответствуют левому и правому плечу.
• Принимается, что искомая линия проходит посередине между этими точками, т. е. через точку х = 0,5×(х_{хлев-плечо}+х_{прав-плечо}). Эти плечевые точки определяют предполагаемую линию, потому что наклонные края приводят к столообразным вершинам и пик из-за шума легко смещается в любую сторону.

Читатели, знакомые с теорией линейных систем, могут убедиться, что этот подход отличается от простой согласованной фильтрации, потому что из той информации, которая имеется на выходе фильтра, берется гораздо больше, чем просто высота пика и его положение. Опыт показал, что более богатые символьные описания лучше подходят для борьбы с типичными явлениями, вызываемыми шумом. Другие примеры содержатся в одной из первых работ по поиску линий, принадлежащей Синфорду и Хорну, а также в программе Хорна, которая призвана определять точное положение интегральной схемы в процессе подготовки к соединению интегральных схем между собой.

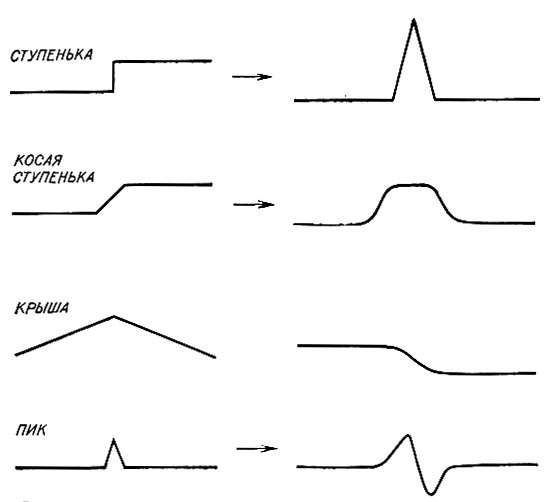
Рис. 8.6. Результаты фильтрации с помощью свертки с так называемой ступенчатой маской, если на входе фильтра 'ступенька', 'косая ступенька', 'крыша' и 'пик'

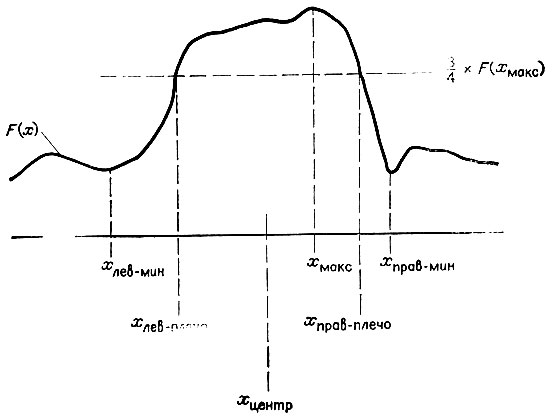
Рис. 8.7. Поиск положения края в профиле после фильтрации. Величины х_макс, х_{лев-мин} и х_{прав-мин} определяют факт присутствия края. Если край присутствует, то предполагается, что х_центр находится посередине между х_{лев-плечо} и х_{прав-плечо}

Для реального мира необходим первичный набросок

Самые сложные системы для мира кубиков были построены в надежде на то, что знания высокого уровня могут быть использованы в программах обработки изображения на входе системы. Например, устройство прослеживания линий Сираи направляется постоянно развивающимися результатами, комбинируемыми с предположениями о возможных формах в мире кубиков. Прослеживание линий и понимание сцен осуществляются совместно друг с другом. Все же не ясно, следует ли в зрительных системах обходиться без эффективного, независимого устройства обработки изображений. Кажется сомнительным, чтобы обширные познания могли заменить внимательное рассмотрение.

Марр высказывает точку зрения, что механизм принятия решений в области зрительного восприятия вообще не должен заниматься рассматриванием изображения, а вместо этого должен оперировать с его символической интерпретацией, первичным наброском.

• Изображения превращаются в первичные наброски посредством процессов, которые позволяют находить, описывать и группировать характерные черты изображения.

Поэтому вычисление первичных набросков напоминает поиск линий, поскольку в обоих случаях используется фильтрация и группирование. Но создание первичного наброска отличается от поиска контурного рисунка в том, что целью является передача более богатого символического описания. Поэтому методы группирования и фильтрации должны быть более сложными.

Вот описание типичных признаков, вычисленное на основе интенсивностей, свойственных точкам изображения:

 (КРАЙ (ТИП ПРОТЯЖЕННЫЙ) 
       (ОРИЕНТАЦИЯ 67.5) 
       (НЕЧЕТКОСТЬ 3) 
       (ПОЛОЖЕНИЕ 271	314))

Чтобы построить такие признаки, Марр начинает с операций фильтрации, обеспечивающих поиск крутых склонов и быстрых изменений наклона. Если такие фильтры применять к не зашумленным одномерным профилям, показанным ранее на рис. 8.5, то выявляются такие характеристические формы, в которых некоторые признаки сохраняются, даже если привносится шум. Одна из таких операций фильтрации напоминает операцию, использованную Сираи при прослеживании линий: каждая точка на выходе является разностью между средним из нескольких точек справа и из нескольких точек слева. Другой фильтр, ответственный за поиск быстрых изменений наклона, более сложен: каждая новая величина образуется путем сложения ближайших точек на входе и вычитания нескольких точек, расположенных непосредственно за пределами центральной группы. Из теории линейных систем известно, что эти операции фильтрации представляют собой свертки изображения с простыми ступенчатыми и столообразными профилями, изображенными на рис. 8.8.

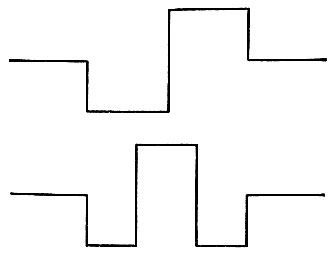
Рис. 8.8. Фильтрация при выделении первоначального наброска сводится к коррелированию наблюдаемых интенсивностей с этими профилями. Первый называется ступенчатой маской, а второй - импульсной маской. Эти корреляции дают аппроксимации для первой и второй производных.

Помогает то обстоятельство, что, по-видимому, имеют значение только пики и их положение на профилях. Первая конфигурация пика на рис. 8.9 соответствует классическому ступенчатому краю. Когда округленная граничная линия разделяет две области, то основную наклонную ступеньку сопровождает отрицательный пик и появляется вторая конфигурация. Для вычисления первичного наброска требуется полный каталог возможностей, подобных этим.

Указанный одномерный результат распространяется на два измерения путем простого повторения одномерного анализа для восьми направлений. Таким образом, каждая точка первичного наброска вычисляется исходя из точек, организованных, как показано на рис. 8.10. (Одномерным операциям, выполняемым многократно, отдается предпочтение по сравнению с двумерными операциями, такими, как вычисление градиента или лаплассиана, и по математическим соображениям, и для принципиальной простоты.)

Уже видно, что создание первичного наброска не может быть дешевой операцией. Многие экспериментировали с менее сложными операциями, надеясь извлечь из изображений хорошую информацию о признаках. Сейчас мы, кажется, начинаем понимать, что недаром биологические глаза выполняют такой сумасшедший объем вычислительной работы.

Результаты, даваемые этими двумя операциями фильтрации, сильно меняются в зависимости от числа точек изображения, которые используются в каждой отфильтрованной величине. Может оказаться целесообразным использование как варианта с широким углом, так и варианта с узким углом для каждого фильтра. Таким образом, в каждом направлении можно применять не два, а четыре или более фильтров. Пугает то обстоятельство, что таким образом каждая точка изображения может породить 4×8=32 профиля. К счастью, влияния, оказываемые соседними ориентациями, являются достаточно несогласованными, так что вместе приходится рассматривать не более четырех профилей.

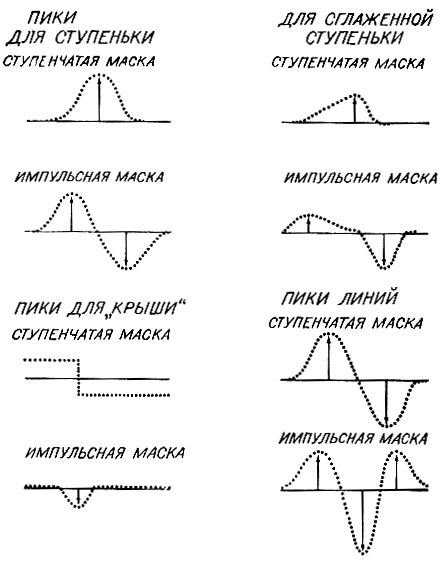
Рис. 8.9. Различные типы краев дают характерные комбинации пиков

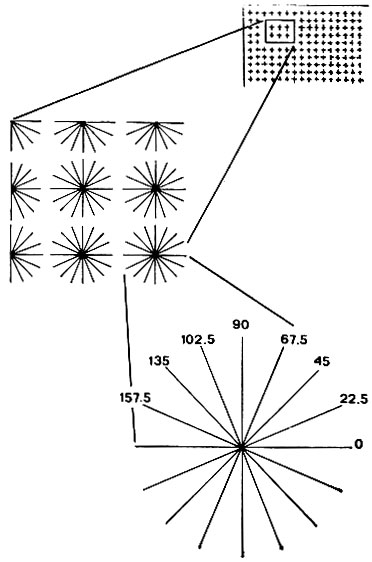
Рис. 8.10. Для вычисления первичного наброска розетки профилей выпускаются в восьми направлениях из точек, выбранных так, чтобы покрыть все изображение

Как только признаки получены, следующей задачей становится их группирование. Естественным первым шагом является связывание соседних точек с точным эталоном типа и ориентации. Получающиеся таким путем нити могут быть продолжены далее с использованием менее строгих критериев. На более поздних этапах группирование производится на основе только положения, и весьма различные элементы могут, комбинируясь друг с другом, давать идентифицируемые группы. Как видно из рис. 8.11, годятся даже концевые точки.

Рис. 8.11. Концы сгруппированных признаков определяют места, которые допускают дальнейшее группирование

На рис. 8.12 показаны группы, найденные на первичном наброске игрушечного мишки. Разумеется, здесь изображены лишь положения признаков и фрагменты линий. Символическое описание содержит также и другую информацию.

Измерения на первичном наброске, по-видимому, определяют воспринимаемую текстуру

Когда мы располагаем первичным наброском, можно заняться исследованием его небольших областей в поиске характерных качеств. Особенно полезны гистограммы интенсивности, длин фрагментов линий, ориентаций фрагментов линий и степени разделимости фрагментов линий. Имеются серьезные свидетельства в пользу того, что воспринимаемая текстура сильно связана с измерениями, выпол* няемыми на этих гистограммах. Согласно такой теории, две текстуры неразличимы, если они порождают одинаковые признаки на гистограммах, несмотря на то что в других отношениях изображения могут значительно отличаться друг от друга. Этот подход, развитый Марром, успешно предсказывает, что одно из изображений на рис. 8.13 содержит отчетливо выделяющийся подквадрат, а второе - нет.

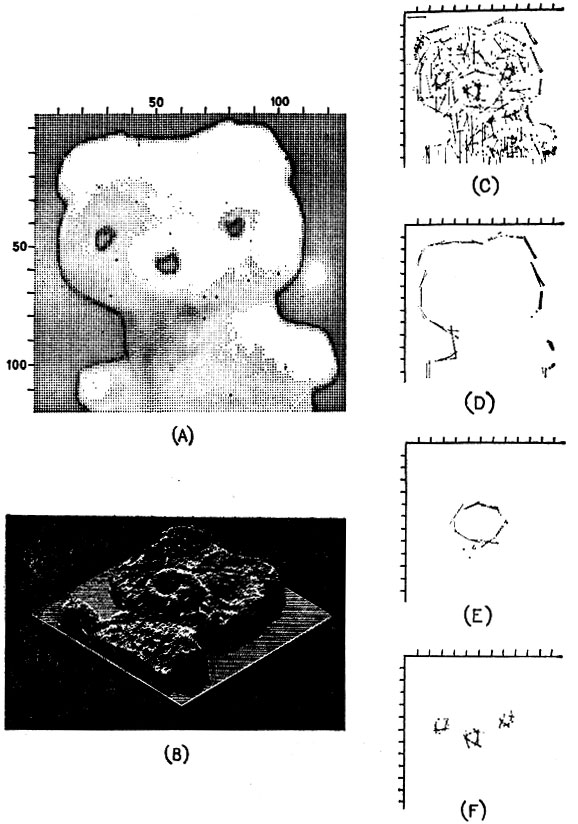
Рис. 8.12. Извлечение первичного наброска. Часть (А) содержит исходное изображение, Часть (В) представляет карту интенсивностей. В части (С) содержатся сегменты первичного наброска до того, как было проведено основное группирование. Части (D - F) показывают группы, найденные на более поздних этапах обработки. (Из работы Дэвида Марра: 'Early Processing of Visual Information', Philosophical Transactions of the Royal Society of London, vol. 275, no 942, October 19.1976, copyright 1976 by the Royal Society, London, England. С разрешения Лондонского королевского научного общества.)

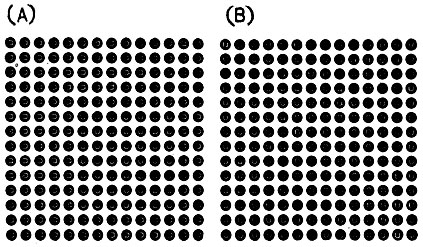
Рис. 8.13. Здесь показаны две текстуры, построенные Юлешом. Они содержат квадратную область, которая отличается от фона. Квадрат резко выделяется на первом рисунке, а на втором - нет. Очевидно, что для разделения необходимо вычислить разность между гистограммами ориентации подквадрата и окружающего его фона. (Из работы: В. Julesc et al., 'Inability of Humans to Discriminate between Visual Textures that Agree in Second-Order Statistics - Revisited', Perception, vol. 2, 1973, copyright 1973 by Pion Limited, London, England. С разрешения Pion Limited и Б. Юлеша.)

Теория Марра более удовлетворительна по сравнению с другими теориями, потому что она полнее соответствует экспериментальным данным и поскольку в ней не используются методы, требующие накопления многомерных гистограмм интенсивностей пар точек изображения. На самом деле нужны лишь одномерные гистограммы, получаемые на основе вычисленного первичного наброска.

Кстати, некоторые виды рыб способны очень хорошо приспосабливать свой внешний вид к окружающей их среде, причем время адаптации не превышает нескольких секунд. Рис. 8.14 показывает, что делают они это весьма эффективно. Очевидно, что эта рыба измеряет некоторые параметры первичного наброска и приводит свою окраску в соответствие с ними путем изменения пятен на спине.

Градиентное пространство позволяет понять ограничения, связанные с освещением

Удивительно мало работ посвящено связи методов искусственного интеллекта с надежным пониманием вопросов освещенности. Однако ясно, что для того, чтобы добиться успеха в проблеме зрительного восприятия, необходимо прийти к пониманию законов физики. "Кустарные" методы, специально развитые для того или иного случая, недостаточно хороши. Недостаточно перебирать методики обработки информации в надежде, что какая-нибудь из них окажется полезной. Следует отдавать себе отчет, что изображения несут большой объем информации о трехмерной природе соответствующих поверхностей. Чтобы эту информацию можно было использовать, важно знать, как формируются рассматриваемые изображения. Это было показано Хорном, который применил дифференциальные уравнения, описывающие освещение изображения, для извлечения информации о форме по градиентам освещенности для простых функций отражения. В дальнейшем, работая с Марром, Хорн обобщил понятие, выработанное Лендом, и показал, что, рассматривая случайную совокупность цветных бумажек, можно установить естественные условия отражения, несмотря на усложнения, вызываемые неодинаковым освещением. Однако в этом направлении основную работу еще предстоит выполнить.

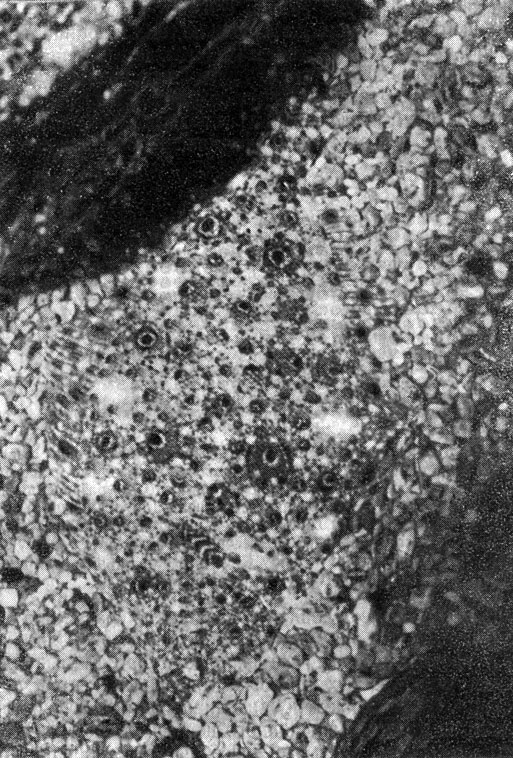
Рис. 8.14. Некоторые виды рыб способны подобрать оттенки пятен на коже так, чтобы текстура соответствовала текстуре океанского дна. Для этого требуется лишь несколько секунд (фотография Б. Зайделя и др. Дж. Леттвина)

Чтобы проиллюстрировать описанные возможности, мы обратимся к исследованию некоторых ограничений, определяемых освещенностью. Поскольку некоторые математические выражения могут показаться незнакомыми, мы слишком далеко заходить не будем, но в то же время было бы неправильно пренебречь всем предметом целиком.

Наш пример послужит объяснением результата, к которому пришел Хорн. Формулируется он весьма просто:

• Ориентации трех поверхностей трехгранного угла можно найти по направлениям линий и наблюдаемых интенсивностей.

К этому результату мы придем косвенным путем. Сначала мы остановимся на определении двумерного преобразования некоторых векторов, задающих ориентацию. Далее мы покажем, что пространство, определяемое таким преобразованием, может помочь установить соответствие между поверхностями и ребрами трехгранного угла. Затем мы рассмотрим соотношение между ориентацией и наблюдаемой яркостью, заметив, что в новом пространстве можно изобразить линии одинаковой яркости. А в заключение мы покажем, что ограничений, поставляемых ребрами и наблюдаемыми интенсивностями, достаточно для определения ориентации поверхности.

Начнем. Точки пространства соответствуют координатным тройкам (x, y, z). Для наших целей удобно представлять себе эти тройки как компоненты вектора xi+yj+zk, идущего в данную точку из начала координат. Принимая такую точку зрения, заключаем, что пространство XY выполняет дополнительные функции, поскольку оно способно отобразить координаты любых векторов, а не только радиус-вектора.

При работе с поверхностями особый интерес представляет единичная нормаль, вектор длины единица, перпендикулярный к поверхности. Если вектор ai+bj+ck представляет собой единичную нормаль, то с может быть найдено по а и Ь, поскольку длина вектора по определению равна единице:

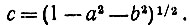
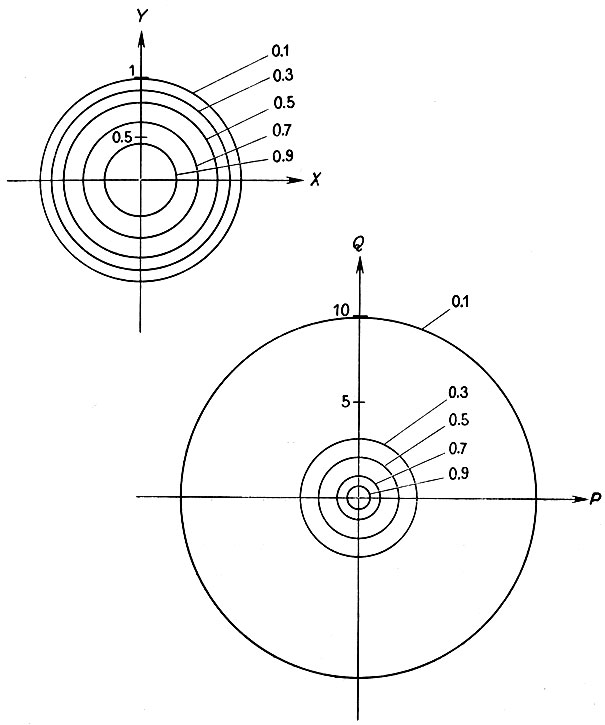
Рис. 8.15. Все единичные векторы лежат и единичном круге в пространстве ХУ. Такого ограничения в пространстве PQ нет. На каждой окружности с, компонента вектора в направлении к, постоянна

Таким образом, направления всех плоскостей в пространстве определяются единственным образом точками пространства XY, лежащими внутри единичного круга, показанного в первой части рис. 8.15.

Определим теперь другое пространство PQ, которое окажется особенно полезным для отображения нормалей к поверхностям. Векторы пространства XYZ отображаются в PQ в соответствии со следующими формулами:

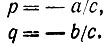
Как показано во второй части рис. 8.15, пространство PQ является как бы раздутым XY. Линии постоянного с являются по-прежнему окружностями, но радиальные направления растянуты так, что каждая точка по всей плоскости PQ соответствует некоторой плоскости с определенной единственной ориентацией, а не только точки, лежащие на единичном круге. Первоначальные компоненты вектора могут быть восстановлены по формулам:

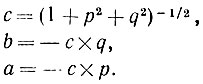
Пространство PQ полезно, несмотря на его изоморфность пространству XY, поскольку оно позволяет выделить сильное ограничение, прежде незаметное:

• Проекция ребра, образованного двумя плоскостями, в пространстве XY перпендикулярна прямой, проведенной между нормальными векторами для этих плоскостей в пространстве PQ.

Это ограничение связывает вместе две плоскости, ребро, образуемое при их пересечении, образы плоскостей в пространстве PQ и образ ребра в пространстве XY. Рис. 8.16 является иллюстрацией. Доказательство, получаемое путем построения векторных и скалярных произведений, утомительное, но не трудное.

Когда имеется не две, а три плоскости, то ограничения на проекции ребра в пространстве XY и положение градиента в пространстве PQ соблюдаются для каждой пары из трех рассматриваемых плоскостей. Отсюда вытекает следующий результат:

• Ребра полностью видимой трехгранной вершины определяют узел типа ВИЛКА в пространстве XY. Грани определяют треугольник в пространстве PQ. Плечи узла типа ВИЛКА перпендикулярны сторонам этого треугольника.

Это то самое ограничение, связывающее ребра и ориентации поверхностей, которое нам необходимо. Очевидно, что ребра определяют треугольник известной формы и ориентации, но неизвестного положения и размеров. Если удастся определить размер и положение, то наша задача решена, поскольку тогда углы треугольника в пространстве PQ дают нормали к поверхностям. Для поиска недостающего ограничения обратимся к яркости.

Наблюдаемая яркость всех плоскостей задается комбинацией положения наблюдателя, условий освещения, материала поверхности, положения поверхности и ее наклоном. В общем случае каждый возможный уровень яркости соответствует семейству возможных ориентаций, которое образует некоторый локус константной яркости либо в пространстве XY, либо в пространстве PQ.

Для конкретности предположим, что расположение наблюдателя, источника света и сцены обусловлено геометрией, изображенной на рис. 8.17. Поскольку предполагается, что сцена достаточно далеко удалена от источника света и наблюдателя, то количество света, падающего на все поверхности, одно и то же. Следовательно, наблюдаемая яркость зависит лишь от угла между поверхностью и направлением пучка света.

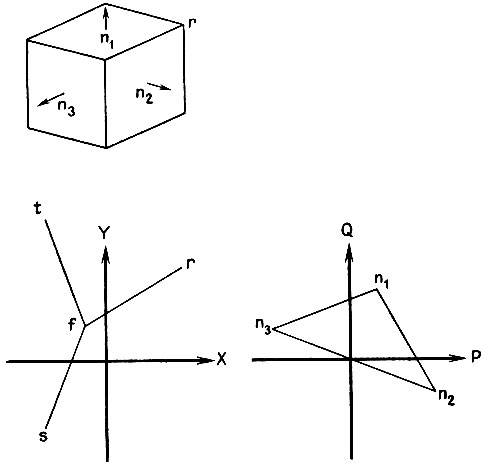
Рис. 8.16. Трехгранная вершина образует линии в пространстве XY и точки в пространстве PQ. Прямые в пространстве XY являются ортогональными проекциями ребер из пространства XYZ. Точки в пространстве PQ представляют векторы градиентов для каждой грани. Можно показать, что прямые в пространстве XY ортогональны прямым, соединяющим градиентные точки в пространстве PQ. Так, fr перпендикулярна

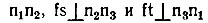
• Для большинства поверхностей наблюдаемая интенсивность изменяется, как косинус угла падения i между нормалью к поверхности и направлением на источник света, достигая максимума, когда поверхность обращена прямо на источник света. Наблюдаемая интенсивность для сферы сходит на нет по мере того, как угол падения стремится к 90° и свет лишь едва касается такой поверхности.
• Для некоторых поверхностей, в частности для поверхности Луны, наблюдаемая интенсивность меняется как отношение косинуса угла i к косинусу угла отражения е между нормалью к поверхности и направлением на наблюдателя. В случае полной Луны i, e равны друг другу в каждой наблюдаемой точке. Следовательно, отношение cos(i)/cos(e) постоянно, наблюдаемая яркость постоянна, затухания по краям нет, и Луна представляется наблюдателю плоской.

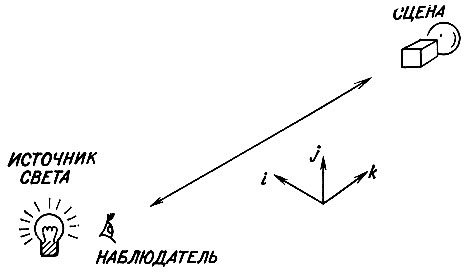
Рис. 8.17. Анализ освещенности упрощается, когда источник света находится вблизи наблюдателя и оба расположены далеко от сцены. Для большинства поверхностей наблюдаемая яркость пропорциональна cos(/), где i - угол падения, измеряемый по отношению к нормали

• Будем работать с нормальными поверхностями и источником света со стороны наблюдателя. Для этого случая косинус весьма удобно представим в виде

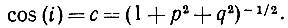
Из этого соотношения видно, что наблюдаемая яркость постоянна, если постоянна величина q²+p². Отсюда линии постоянной яркости в пространстве PQ представляются в виде окружностей, как изображено в первой части рис. 8.18. Это естественно, потому что постоянство величины с при изменении всех остальных компонент нормального вектора к некоторой поверхности сводится к вращению поверхности вокруг оси, совпадающей с направлением на источник света.

Конечно, при ином расположении наблюдателя, источника света и рассматриваемой сцены получатся другие кривые постоянной яркости. На второй части рис. 8.18 показано, что получится, когда направление на источник света составляет с направлением на наблюдателя угол примерно 37°.

Теперь мы можем свести все вместе. Мы получили, что форма и ориентация треугольника в пространстве PQ определяются ребрами наблюдаемой трехгранной вершины. У нас имеется наблюдаемая яркость поверхностей, которые соответствуют углам этого треугольника. Для того чтобы найти ориентации поверхностей, следует перемещать и изменять размеры треугольника до тех пор, пока его вершины не лягут на контура равной яркости, соответствующие величинам наблюдаемой яркости.

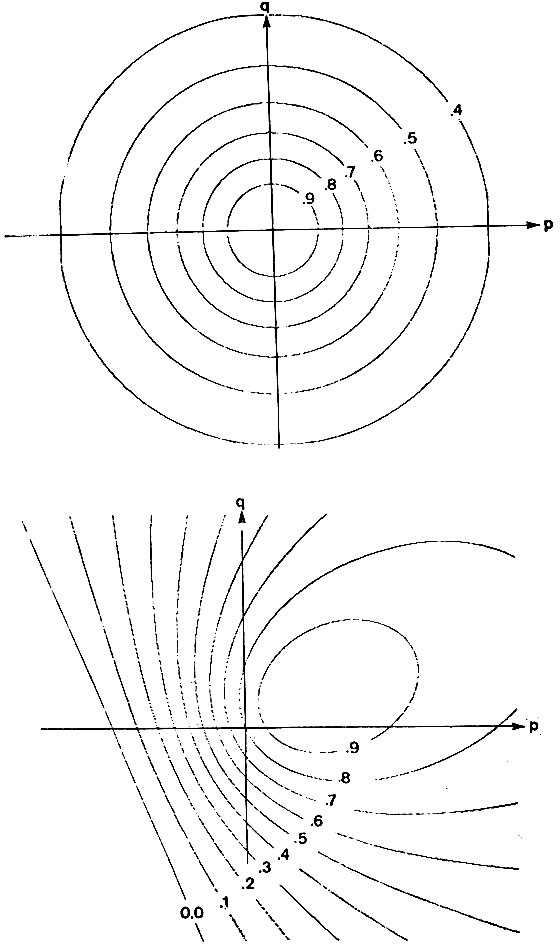
Рис. 8.18. Линии постоянной яркости для поверхностей, где яркость пропорциональна cos(i), i - угол падения. Числа, которыми помечены линии, отвечают различным величинам cos(f). Первое множество соответствует случаю, когда источник света расположен близко к наблюдателю, а второе - случаю, когда угол между направлением на источник света и направлением на наблюдателя равен 37°

Наблюдаемая яркость дает также ориентацию поверхностей и для криволинейных предметов, но для этого необходимо решение некоторой системы дифференциальных уравнений в частных производных. Результирующая теория позволяет объяснить, как работает косметика. Румяна позволяют затенить на краях слишком широкое лицо, благодаря чему оно выглядит несколько уже.