Глава 3. Анализ некоторых временных образов
3.1. Изображение на временной оси
Временные образы определяются при помощи образующих типа соответствия: их можно задавать как функции на действительной оси, которые принимают значения из некоторого сопоставленного пространства. Имеется множество разновидностей временных образов, для которых то обстоятельство, что они заданы через некоторый параметр "времени", не имеет отношения к делу, и их анализ с тем же успехом можно проводить, не обращаясь к каким-либо дополнительным опорным пространствам.
В данной главе мы сосредоточим внимание на одном определенном аспекте временных образов, отложив остальные до следующих глав. Здесь опорное пространство -действительная ось. Это структура с очень богатыми возможностями, и она может служить основой для столь многих математических построений, что мы сможем рассмотреть лишь наиболее "времяподобные" аспекты.
Поскольку действительная ось образует абелеву группу относительно сложения, то мы, естественно, приходим к фурье-характерам как (комплексным) тригонометрическим функциям, являющимся основой анализа Фурье. Анализ Фурье - определенно один из важнейших инструментов при анализе образов, однако заниматься этой проблемой в данной главе нецелесообразно, так как большую часть материала можно непосредственно обобщить на опорные пространства других типов. Так, например, R2, R3, . . и их подгруппы также являются абелевыми группами относительно сложения и, следовательно, методы анализа Фурье применимы. Многие опорные пространства других типов имеют групповую природу, хотя и необязательно абелеву, что усложняет анализ Фурье. Очевидно, что групповые свойства R1 как опорного пространства не заслуживают того, чтобы мы занимались им в данной главе.
Аналогично известны временные образы, в основе которых лежит то обстоятельство, что R1 является носителем важной разновидности σ-алгебры - борелевских множеств -и может служить носителем мер, порождающих пространства Lp. Это обстоятельство, однако, также относится к категории свойств, поддающихся естественному обобщению на опорные пространства других типов.
Вместо этого мы остановимся на том свойстве, что пространство R1 полностью упорядочено, и будем проводить анализ образов, основываясь именно на этом факте. Структура связей образующих не всегда будет симметричной, и потому входные и выходные связи следует рассматривать по отдельности. Тип соединения будет обладать лево-правой асимметрией, как будет сейчас показано.
Физическая интерпретация "времени" может варьироваться. Очевидно, во-первых, что удобнее, если время принимает дискретные значения, скажем целые числа, а не континуум значений на действительной оси. Иногда к тому же мы будем придавать "времени" смысл, отличающийся, строго говоря, от "физического" времени. Так, в частности, в разд. 3.4 "время" будет представлять собой число выполненных команд в процессе выполнения программы ЭВМ. Если машина работает с постоянной интенсивностью выполнения команд без прерываний, то "время" пропорционально физическому, но это справедливо только в указанных условиях. В разд. 3.2 временной параметр представляет собой просто счетчик, показание которого изменяется на единицу при выполнении арифметической операции, так что связь с физическим временем становится еще более условной.
Возвращаясь к типу соединения регулярных временных конфигураций, отметим, что он будет выбираться так, чтобы все стрелки были нереверсивными и указывали направление увеличения времени, а входная арность была постоянной и равной постоянной выходной арности. Величина подобной постоянной арности ωiu = ωout зависит от выбора сопоставленного пространства, и мы будем стараться, чтобы оно было достаточно богатым и позволяло нам работать с арностями ωin = ωout = 1. Последнее означает, что уравнение системы, описывающее изменение образа во времени, имеет единственное решение при t > t0, если известно соответствие при t = t0 - задача Коши должна быть тщательно сформулирована. В таком случае входная связь образующей в интервале (а, b) задается как (а, y(а + 0)) и выходная связь - как (b, y (b - 0)).
При работе с диффузными образами естественно допускать, что элементами сопоставленного пространства являются распределения вероятностей на соответствующем пространстве состояний.
Отношение связи для двух образующих g1 и g2 в интервалах [a1, b1] и [a2, b2] означает, что если стрелка направлена от g1 к g2, то b1 = а2 и g1 (b1 - 0) = g2 (а + 0). Это условие непрерывности применимо к непрерывному времени, но если время дискретно, то его следует модифицировать, скажем, следующим образом. Пусть сопоставленное пространство Rp. Рассмотрим две образующие на двух дискретных интервалах [а1, b1] и [а2, b2] с целыми числами в качестве концевых точек. Если соединяющая стрелка направлена от g1 к g2 то должно означать, что b1х + 1 = а2 и значения соответствий y(b1) = (y11, y22,...,y1p) и y(а2) = (y11, y12,...,y1p) должны удовлетворять условию y22 = y11, y23 = y12 ,..., y2p = y1p-1. Интерпретация этого условия заключается лишь в том, что рассматривается вектор y(t), который должен быть составлен из значений f(t), f(t - 1), ... , f(t - p + 1) некоторой функции времени f, что и приводит к выписанным выше соотношениям. Можно воспользоваться и другой кодировкой-например, считать компонентами вектора у функцию f (t) и разности f порядка 1, 2, 3, ..., р - 1, причем трактовка остается аналогичной. Очевидно, что отношения связей такого типа инвариантны относительно преобразований подобия, состоящих из переносов временной оси.
Выше мы убедились в том, что этот тип отношения связей минимально удовлетворительный. Иногда отношение согласования р указывает также, каким образом соотносятся индексы классов непрерывных образующих.
В конечном счете регулярные конфигурации будут идентифицироваться как функции (см. разд. 3.1, т. 1). Полученные в результате изображения относятся к классу режимов. Изображение I соответствует некоторому интервалу [а, b] временной оси. Конфигурация c = (g1, g2,...,gn)∈I соответствует разбиению a = a0 < a1 < a2 <...< an-1 < an = b, а образующие gi представляют функции, заданные на [ai-1, a], i = 1, 2, ..., n, связанные отношением согласования ρ. Естественно, аi и gi не должны однозначно определяться I, и потому задача сегментации (см. т. 1, разд. 3.1) может иметь несколько решений.
Как и при синтезе образов, в принципе можно либо рассматривать образующие как функции, полученные в результате рассмотрения каждого конкретного изображения, либо изучать конфигурации и изображения, порождающие ансамбль временных образов. Первый из этих подходов приводит к конструкции, описанной выше.
При втором подходе мы вводим в качестве образующих некоторое множество линейных операторов T преобразующих множество Y в себя (дискретное время), или множество однопараметрических полугрупп {Тt, t > 0} (непрерывное время). В случае непрерывного времени удобно для определения полугруппы использовать инфинитезимальную образующую Г:
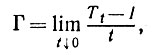(3.1.1)
где I - единичный оператор. Предельный переход в выражении
(3.1.1) следует интерпретировать таким образом, чтобы образующая Г имела смысл.
Схема конфигурации тогда может иметь, например, такой вид, как схема, представленная на рис. 3.1.1. На этой схеме отношение связи показывает, как следует выбирать индексы класса образующих следующих друг за другом операторов Т. Отметим, что эта схема конфигурации отличается от схем, описывающих любую полученную в результате временную конфигурацию: она обладает циклическим типом соединения (а не линейным), включает фиксированное число образующих (а не ограниченное) и образующие являются операторами (а не функциями действительной переменной). Выбор определенного типа конфигураций зависит от того, изучаем ли мы некоторое определенное временное изображение (или конфигурацию) или занимаемся непосредственно синтезом ансамбля изображений.
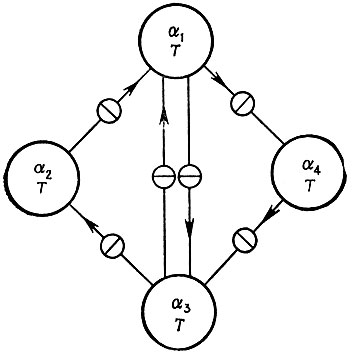
Рис. 3.1.1
Следует отметить, что схема, приведенная на рис. 3.1.1, представляет некоторую конфигурацию, порождающую временные образы. В том, что ее тип соединения отличается от типа соединения порожденных ею объектов, нет никакого противоречия. Сравните, например, с диаграммой конечного автомата, порождающего линейные цепочки.
Совершая проход по представленной на рисунке схеме конфигурации и следуя все время только по допустимым (отмеченным) ветвям, получаем, например, последовательность операторов Тα1, Тα2 ..., Tαn. Тогда, если исходным является интервал y1 то идеальное изображение мы получаем в виде вектора y с компонентами
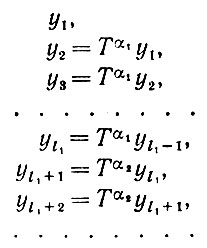(3.1.2)где l1, l2, ... - продолжительности режимов, а временной интервал изображения представляет собой некоторый заданный дискретный интервал [а, b].
В случае непрерывного времени аналогично получаем идеальное изображение y(t) на некотором интервале [а, b], причем y(а) = yin и
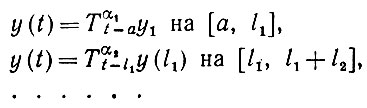(3.1.3)Идеальное изображение режима необязательно однозначно определяет соответствующие режимы - его образующие не обладают единственностью. Если образующие g1 и g2 соединены стрелкой, направленной от первой ко второй, и если им соответствует одно и то же Т, то g1 и g2 сливаются в новую образующую g: соответствующий режим распространяется на объединение интервалов, которые служат опорными множествами для g1 и g2 (см. т. 1, разд. 3.1). Этот факт можно использовать для приведения конфигурации, см. теорему 3.1.2, т. 1.
Рассмотрим изображение I, определенное на дискретном интервале [а, b], который состоит из целых чисел а, а + 1, а + 2, ..., b - 1, b: рассмотрим это изображение с точки зрения анализа изображений (см. разд. 1.1). Каждому переходу t → t + 1 поставлен в соответствие некоторый оператор Т из множества А, которое для простоты предполагается конечным. Число переходов равно l = b - а, так что изображение I можно представить с помощью регулярной конфигурации, содержащей l образующих. Если бы можно было слить пары образующих, то численная сложность была бы снижена, и, следовательно, существует наименьшее число lmin, соответствующее l:
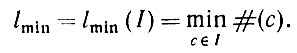(3.1.4) Для того чтобы выяснить, как вычисляется lmin, рассмотрим
один из переходов t → t + 1, t - a, a + 1, ..., b - 1. Значения у должны удовлетворять условию yt+1 = Тyt так что оператор должен выбираться из множества
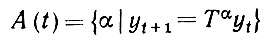
и иметь индекс класса образующей α(t). Множество A(t) не может быть пустым, так как в этом случае конфигурации, составляющие основу I, не были бы регулярными. Если это множество содержит единственный элемент, то очевидно, что α(t) должен быть равен этому элементу. В противном случае α(t) не однозначно определяется через I.
Пусть α(t) - селекторная функция, a(t)∈А (t), t∈[а, b]. Число режимов для соответствующей конфигурации тогда равно
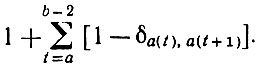(3.1.5)
Воспользуемся теперь методом динамического программирования для определения lmin. Применим следующий алгоритм приведения. Пусть
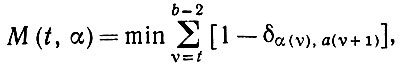(3.1.6)где минимум берется по всем селекторным функциям a(υ) с элементами из A(υ), a(t) = α. Имеет место рекурсия
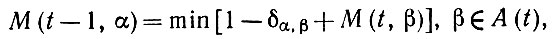(3.1.7)что дает возможность определять М (1, α) для t, лежащих в обратном направлении. Когда М(1, α) известно, остается лишь провести минимизацию по α для того, чтобы найти одну (их может быть несколько) несводимую по модулю R конфигурацию, имеющую минимальную численную сложность.
Может, конечно, оказаться, что yt+1 = Tyt всегда однозначно определяет Т посредством некоторого значения α из A и тогда алгоритм приведения не требуется. Можно говорить и о более общем случае, когда знание yt, yt+1, ..., yt+r+1, где
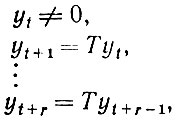(3.1.8)определяет Т. Отметим, что во всех выписанных выше r уравнениях используется один и тот же оператор Т. Насколько же большим следует выбирать r для того, чтобы сформулированное утверждение выполнялось?
Для того чтобы изучить эту проблему, допустим, что операторы Тβ - линейные, и отображение Y = Rp → Rp. Это означает, что значение Tz известно для z1 = yt, z2 = Tyt, z3 = T2yt,..., zr = Tr-1yt, и, следовательно, если R? натянуто на векторы z, при r = р единственность будет иметь место. Не всегда, однако, это будет так. Если, например, yt оказывается собственным вектором соответствующего оператора Т, то утверждение несправедливо. Необходимо несколько более сильное условие.
Теорема 3.1.1. Пусть операторы Тα не имеют общих собственных значений. В таком случае знание z1 = yt z2 = Tyt, z3 = T2yt, ..., zp+1 = Tpyt однозначно определяет T для любого ненулевого вектора yt.
Доказательство. Введем для произвольного β характеристический многочлен
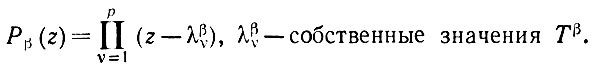(3.1.9)Тогда
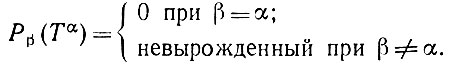(3.1.10)Первое утверждение в (3.1.10) является классическим (см., например, монографию Мак-Даффи (1946), с. 18). Второе утверждение (3.1.10) справедливо, поскольку собственные значения Pβ(Тα) имеют вид (μ = 1, 2, ..., p)
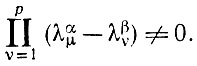(3.1.11)Записав характеристические многочлены в виде
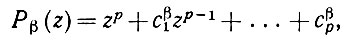(3.1.12)устанавливаем, что линейная комбинация
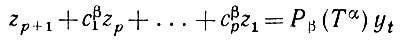(3.1.13)
должна быть равна нулю при β = α и не равна нулю в остальных случаях. Необходимо, следовательно, просто оценить выражение (3.1.13) и найти значение (единственное) β, при котором оно обращается в нуль. Это значение β и является истинным индексом класса образующих.
В качестве примера укажем, что если операторы Т имеют описанный выше вид, когда yt представляет значения функции в моменты времени t, t - 1, ..., t - p + 1. то матрица для всякого Т является сопутствующей:
(3.1.14)и ее характеристическое уравнение-просто:
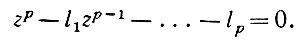(3.1.15)Остается, следовательно, вычислить значение линейной комбинации
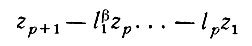(3.1.16)и применить описанную выше процедуру. Это гарантирует единственность, если корни характеристического уравнения (3.1.15) не имеют общих значений для различных индексов класса образующих.
Теоремой 3.1.1 можно воспользоваться, чтобы уменьшить объем вычислений при реализации алгоритма приведения тогда, когда длина всех режимов равна по меньшей мере р. В таком случае для каждого t множество A(t) содержит самое большее р+1 значение, поскольку t должно принадлежать режиму, не имеющему разрывов, по крайней мере на [t - р, t], или [t - p + 1, t +c1], или ...[t, t + p]. Если р мало, то можно добиться существенной экономии времени счета. Отметим, что условие, налагаемое на длину режима, является условием, ограничивающим численную сложность конфигураций.
Как правило, при анализе образов легче работать с одноатомными конфигурациями. Поэтому ниже в данном разделе мы ограничимся самым элементарным рассмотрением только этого случая, а к общему случаю обратимся в разд. 3.2.
Когда изображение в целом эквивалентно отдельной образующей по модулю R, то соответствующий временной образ порождается некоторым фиксированным механизмом: это случай временной однородности. Поведение результата будет рассматриваться в терминах сходимости - расходимости yt при больших значениях t. Мы выделим четыре основных типа асимптотического поведения.
Тип I. Сходимость. Предел yt существует при t, стремящемся к бесконечности. Если порождающий механизм случайный, то термин "предел" следует рассматривать, например, как сходимость по вероятности, в среднем или почти наверное. Сходимость же по распределению не будет считаться принадлежащей этому типу.
Пример 1. Рассмотрим цепь из сопротивлений и емкостей, схема конфигурации которой приведена на рис. 3.1.2, а. Две образующие, емкость С и сопротивление R, соединены отношением связи, указывающим, что падения напряжения на R и С одинаковы. Общее падение напряжения в момент времени t
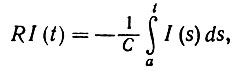
следовательно, CRI + I = 0 и
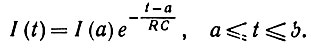(3.1.17)
Временной образ представляет собой просто экспоненциальную кривую. Когда b = +∞ и t → ∞, величина тока приближается к нулю.
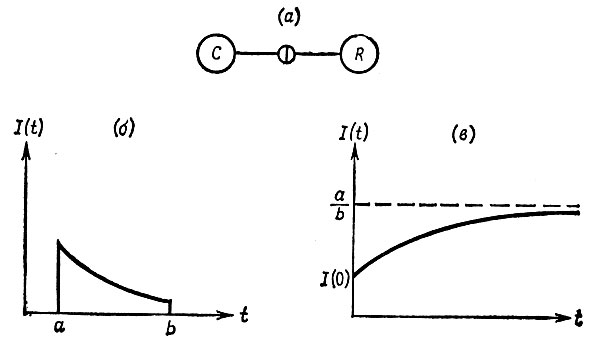
Рис. 3.1.2
Пример 2 (рост при ограниченных ресурсах). Пусть I(t) - размер популяции, а темп относительного прироста равен а - bI(t) при I(t) ≤ а/b. Уравнение системы в таком случае имеет вид
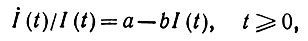(3.1.18)
и, следовательно,
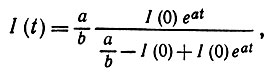(3.1.19)так что I(t) → (а/b), как это показано на рис. 3.1.2, в. В данном случае наблюдается сходимость к уровню насыщения а/b.
Тип II. Тенденция к повторению. Значения I (t) не сходятся, но обнаруживают точно или приближенно периодическое поведение. "Приближенную периодичность" можно интерпретировать многими способами, некоторые из которых будут затронуты ниже.
Пример 3 (гармонический осциллятор). Это, возможно, простейший и наиболее важный изо всех временных образов. Пространство состояний Y = R2, а инфинитезимальная образующая Г определяется линейным оператором в матричной форме:
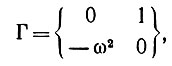(3.1.20)где y1 и y2 интерпретируются соответственно как функция от времени и ее производная. Следовательно, функция времени y1 удовлетворяет уравнению
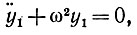
так что
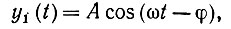(3.1.21)где амплитуда А и фазовый угол φ произвольные, но частота со и период Р = (2π/ω) фиксированы.
Пример 4 (нелинейный осциллятор). Если возвращающая сила нелинейна, то все еще могут получаться периодические решения, однако, как правило, период Р уже не фиксирован, а зависит от амплитуды. Когда механизм двухступенчатый, причем на каждой ступени возвращающая сила есть аналитическая функция, возникают релаксационные колебания и функция времени принимает более или менее пилообразную форму. Мы рассмотрим один случай такого типа в разд. 3.5.
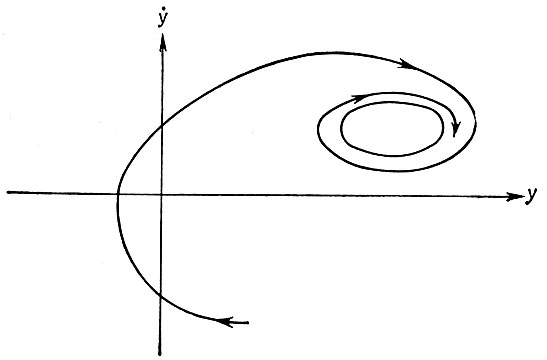
Рис. 3.1.3
Пример 5 (предельный цикл). Образы, являющиеся не строго, но лишь асимптотически периодическими, могут возникать в системах, поведение которых описывается нелинейными дифференциальными уравнениями. Поведение системы, описываемой уравнением второго порядка, можно представить на фазовой плоскости (y, y⋅), как это схематически показано на рис. 3.1.3, где траектория приближается к внутренней замкнутой кривой. Для простоты мы представили на рисунке только одну траекторию.
Пример 6 (вынужденные колебания). То же самое, что и в случае гармонического осциллятора, за исключением того, что механизм включает линейный член, представляющий трение. Колебания вынуждаются возмущающим фактором в виде белого шума. Уравнение колебаний имеет вид
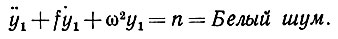(3.1.22)
Применение стандартного спектрального анализа к этому уравнению приводит к следующему:
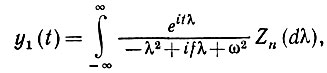(3.1.23)
где Zn - спектральный процесс, соответствующий шумовой составляющей. Следовательно, спектральная плотность y1 равна
(3.1.24)
Если, таким образом, f мало, то пики этой плотности приходятся на λ = ±σ. Итак, функция y1 будет вести себя как (почти) гармонический осциллятор на коротких временных интервалах. На более длинных интервалах, однако, отсутствие строгой периодичности становится очевидным.
Представляет интерес случай, когда временной образ порождается стационарным процессом восстановления на временной оси, скажем, с распределением F временных промежутков между событиями (см., например, монографию Феллера (1957), т. 2, гл. 11). Форма импульса определяется функцией φ, а изображение - суперпозицией импульсов, расположенных в точках (моментах) событий tυ процесса восстановления, так что
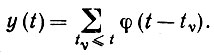(3.1.25)Для сходимости (3.1.25) мы потребуем, чтобы распределение F имело конечное среднее значение и чтобы φ принадлежала L1 или L2 на действительной оси. Результат (3.1.25) называется образом восстановления. Если, в частности, распределение F сосредоточивается в одной точке, так что все временные промежутки между событиями tυ+1 = tυ одинаковы, и если начальная фаза случайная, что обеспечивает стационарность процесса y, то возникает строго периодическое изображение. Если распределение F не очень сильно сконцентрировано относительно среднего значения, то возникают изображения, являющиеся не строго, но лишь приближенно периодическими.
Пример 7 (образы Лиссажу). Движение двух гармонических осцилляторов, например
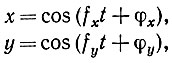(3.1.26)на плоскости ху обнаруживает интересные формы поведения. Если обе частоты равны fx = fy = f, то очевидно, что как х, так и y являются линейными функциями от cos ft и sin ft. Следовательно, (х, y) располагается на коническом сечении, которое вырождается в окружность при разности фаз φx - φy = π/2 или 3π/2 и прямую при φx - φy = 0 или π В остальных случаях это эллипс.
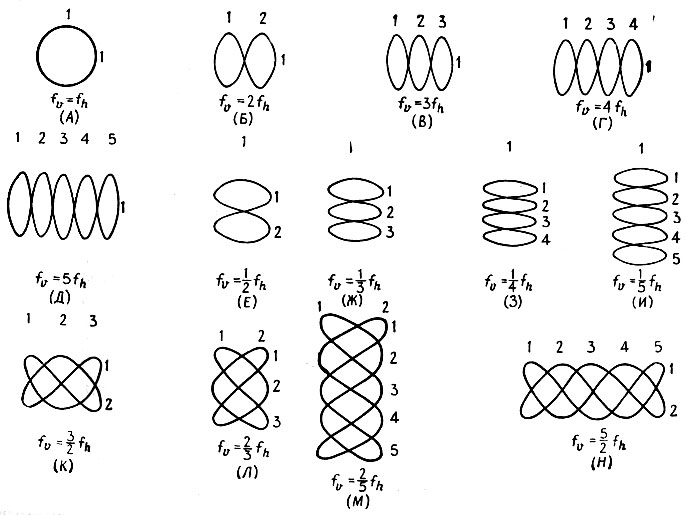
Рис. 3.1.4
Если отношение fx/fy не равно единице, но представляет собой рациональное число, то возникают более сложные образы. Используя формулы сложения тригонометрических функций, все еще можно записывать х и y как линейные функции от некоторых степеней cos ft и sin ft где fx и fy представляются как кратные f частоты. Это означает, что образ - все еще алгебраическая кривая, но может представать во многих формах. Эти образы известны как фигуры Лиссажу; несколько примеров таких фигур приведено на рис. 3.1.4 (они заимствованы из справочника Тернера (1965) с. 161)). Заметим, что число вертикальных и горизонтальных контуров указывает, каково отношение частот, и, следовательно, дает возможность просто и быстро определять это отношение. Таким же образом в предыдущем случае fx = fy фазовый угол φx можно определить, подстраивая второй фазовый угол до тех пор, пока образ не выродится в линию.
И наконец, если отношение частот иррационально, то очевидно, что образ заполняет весь квадрат. В самом деле, если в уравнении fxt + φx = u + 2πk фиксировано u, то, выбирая большие значения k, можно сделать
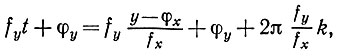
при приведении по модулю 2π сколь угодно близким к любому числу в диапазоне (0,2π). Это следует из того факта, что числа (fy/fx)k, приведенные по модулю 1, равномерно распределены на (0, 1) (см. ниже обсуждение примера 9). Следовательно, образ будет чрезвычайно хаотическим. При представлении на экране электронно-лучевой трубки с конечной постоянной времени люминофора этот образ будет казаться вращающимся.
Тип III. Эргодическое поведение. Функция y(t) не устанавливается на каком-либо конкретном значении или цикле, хотя ее распределение сходится к некоторому пределу. Такие временные образы очень подробно изучены в эргодической теории (см., например, работу Хопфа (1948), в которой можно найти соответствующие детали). Конечно, здесь мы сможем привести лишь несколько примеров из этой богатой математической теории.
Обычно, хотя это и не обязательно, начинают с предположения о существовании в пространстве Y ограниченной меры m, являющейся левоинвариантной относительно оператора Т. Если f - функция класса Li относительно меры m на Y, то основная эргодическая теорема утверждает, что среднее по времени
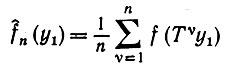(3.1.27)
сходится почти для всех начальных значений y1. Если предел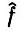 
- почти наверное постоянная, так что он совпадает со средним значением f, если m(Y) нормирована к 1 и это справедливо для всех f, то говорят, что оператор Т эргодический.
Для того чтобы это было верно, конечно, необходимо, чтобы оператор Т обнаруживал тенденцию "перемешивать" Y и порождать беспорядок. Выражаясь более точным языком, говорят, что оператор Т метрически транзитивен, если не существует ни одного измеримого множества E⊂Y, инвариантного относительно Т, за исключением тривиальных множеств Е = ∅ и Е = Y.
Старые результаты эргодической теории утверждают, что именно метрическая транзитивность служит необходимым условием эргодичности. Рассмотрим несколько примеров.
Пример 8 (генераторы случайных чисел). Пусть Y =[0, 1] - одномерный тор, полученный путем отождествления точек 0 и 1, периодический, с лебеговой мерой m. Определяем Т как
(3.1.28)Легко показать, что для любого борелевского множества У имеет место m(T-1E) = m(E), и, следовательно, Т сохраняет меру. Можно доказать его метрическую транзитивность. Следовательно, поведение последовательности {Tυy1; υ ≥ 1} будет хаотическим, как и утверждает эргодическая теорема. Выбирая, например, f как индикаторную функцию интервала [a, b] ⊆ Y, получаем, что почти для всех значений справедливо
Асимптотическое распределение последовательности {Tυy1) равно равномерному распределению на Y почти для всех начальных значений yt.
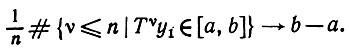(3.1.29)Это обстоятельство имеет ряд важных практических последствий для генерации псевдослучайных чисел. Поскольку цифровая вычислительная машина является дискретным устройством, вышеизложенное требует новой интерпретации. Допустим, что одномерный тор заменен циклической группой порядка N, где N-очень большое целое число, и определение оператора Т, данное в (3.1.28), заменим следующим:
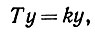(3.1.30) приведенному к множеству {0, 1,2, ... N - 1} по модулю N, где k - натуральное число. Отметим, что приведение в (2.1.30) в вычислительном отношении несложно при использовании переполнения по крайней мере в тех случаях, когда N выбирается равным 2w для машин с длиной слова w. В таком случае итерационное применение Т к начальному значению y1 позволяет получить последовательность целых чисел, заключенных между 0 и N - 1. Конечно, переход от непрерывного к дискретному пространству Y является довольно тонким, и поэтому следует проявлять осторожность при выборе соотношения между k и N. Вычислительная схема (3.1.30) известна как мультипликативный конгруэнтный генератор псевдослучайных чисел, она имеет большое практическое значение.
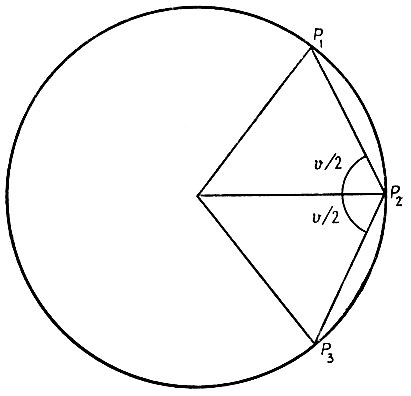
Рис. 3.1.5 а
Рис. 3.1.5 6
Алгоритм (3.1.30) можно реализовать с помощью программы, состоящей всего из нескольких команд. Настораживает тот факт, что столь простая программа позволяет порождать последовательности, которые мы хотим наделить по крайней мере некоторыми "случайными" свойствами, т. е. лишить регулярности. Несмотря на это психологическое недоверие, алгоритмы такого типа обеспечивают практический успех.
Хорошо известно, что если консервативная механическая система представлена в обобщенных координатах (q, р) гамильтоновой механики, то мера Лебега в этом фазовом пространстве инвариантна относительно движения. Этот факт известен как теорема Лиувилля (см., например, монографию Хинчина (1943)).
Это означает, что средние по времени типа (3.1.27) сходятся, если f - функция класса в фазовом пространстве. Интегральные инварианты типа полной энергии или полного момента позволяют естественным образом сузить рассуждения на многообразия, в которых эти интегралы принимают постоянные значения. Как правило, чрезвычайно трудно ответить на вопрос, является ли рассматриваемая система эргодической или нет.
На рис. 3.1.56 представлен небольшой пример, полученный следующим образом.
Пример 9 (движение с упругими соударениями). Материальная точка совершает равномерное движение внутри некоторой окружности, это движение нарушается лишь упругими соударениями со стенками.
Если первый угол соударения со стенкой представить величиной υ/2, измеренной от нормали в точке удара (см. рис. 3.1.5а), то очевидно, что длина дуги между очередными ударами равна просто радиусу, умноженному на π - υ. Если эта величина оказывается несоизмеримой с периметром окружности 2π, т. е. 2π ≠(π - υ)× рациональное число, то можно ожидать, что точки соударения распределены равномерно. Это следует из классической теоремы Вейля о том, что последовательность α, 2α, 3α, ... , где α - иррациональное число, приведенная к [0, 1] по модулю единица, распределена равномерно.
В приведенном выше примере склонность к хаотичности подобного сорта проявляется на рис. 3.1.56, причем траектория заполнит круговое кольцо целиком, если упомянутая выше несоизмеримость имеет место.
Отметим, что построение последовательности α, 2α, 3α, . .. соответствует случаю аддитивного конгруэнтного генератора псевдослучайных чисел.
Тип. IV. Расходимость. Рассмотрим теперь функции, которые резко возрастают с увеличением времени. Простого примера будет достаточно для иллюстрации этого поведения.
Пример 10 (рост с постоянной скоростью). Пусть Y = R, и допустим, что y(t) измеряет размер популяции, который увеличивается с постоянной скоростью r. Если мы пользуемся понятием абсолютно о прироста у = г, то получаем линейный рост, т. е. y = rt + a. Если речь идет об относительном приросте y⋅/y = r, то получаем экспоненциальный рост, т. е. y = aert. В обоих случаях размер популяции просто беспредельно увеличивается, не обнаруживая при этом ни периодичности, ни хаотичности.
|
ПОИСК:
|
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'