3.5. Образы возбуждения нейронов

Рассмотрим идеализированные нейроны, которые пораждают временные образы. Допустим, что электрические свойства нейрона представлены контуром RC, параллельно которому включено устройство мгновенного действия с релейной характеристикой (см. рис. 3.5.1; здесь U = U (е) -входное напряжение).

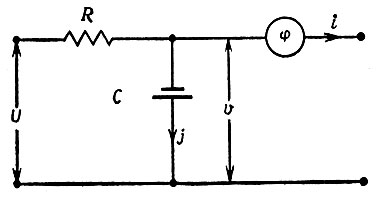
Рис. 3.5.1

Точнее, это означает, что нервная клетка представлена контуром, в котором R - это сопротивление и С - емкость. Ниже входное напряжение U = U (t) всегда предполагается неотрицательным, а выходной ток обозначен как i = i(t). Ток в первом контуре цепи обозначен через j = j (t), а напряжение на конденсаторе - через υ = υ(t).

Нелинейное устройство будет иметь характеристику φ:

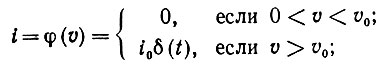(3.5.1)

здесь i₀ > 0 постоянная; устройство имеет только два состояния - выключено и включено.

Тогда выходной сигнал проходит по линии передачи, действующей как фильтр LRC, до тех пор, пока он не достигает точек соединения с другими клетками. Присоединим пока к выходным концам цепи миллиамперметр, так что в сущности они окажутся закороченными, и посмотрим, как будет себя вести выходной сигнал.

Несмотря на простому схемы, выходные характеристики оказываются интереснее, чем могло показаться с первого взгляда. Для их изучения воспользуемся просто законом Ома, получив в результате

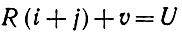(3.5.2)

и, исходя из определения емкости,

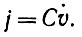(3.5.3)

Исключая j и воспользовавшись условием (3.5.1), получаем

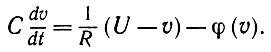(3.5.4)

В качестве начальных условий для (3.5.4) примем t = 0 и υ = υ(0) < υ₀. Тогда получаем, что

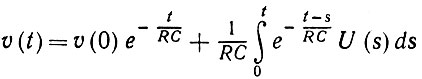(3.5.5)

до тех пор, пока υ(t) < υ₀. Если входной сигнал достаточно велик, то критический уровень υ₀ в конце концов будет достигнут. Когда это произойдет, скажем в момент времени Т (значение некоторого функционала Т(U)), появляется мгновенный импульс тока. Затем напряжение на конденсаторе уменьшается на величину i₀/C и принимает новое значение υ(Т) - i₀/C = υ₀ - i₀/C. Интегрирование уравнения (3.5.4) на малом временном интервале показывает, что сила импульса тока равна i₀.

Другими словами, нервная клетка находится в состоянии покоя вплоть до момента времени t = Т; в этот момент она переходит в возбужденное состояние и напряжение мгновенно падает. Такое поведение имеет циклический характер, причем продолжительность цикла Т (U) зависит от функции времени U = U(t). Можно, следовательно, ожидать, что продолжительность цикла будет флуктуировать.

Чтобы лучше понять это явление, можно выразить входные потенциалы через критический уровень υ₀ = υ₀ - i₀/C, т. е. записав уравнение U = υ₀ + υ. Тогда уравнение (3.5.5), если принять в качестве начального значения υ(0) = V₀, приобретает вид

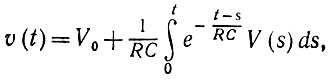(3.5.6)

и Т = Т (U) - (первое) решение уравнения

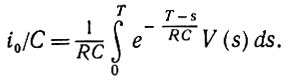(3.5.7)

Как же ведет себя величина Т (V), если для того, чтобы получить V (t), на вход подается периодическая последовательность импульсов? Какова, в частности, выходная характеристика для установившегося режима, наступающего по окончании переходного процесса? Пусть амплитуда импульса равна SP, а период равен Р. Может оказаться, хотя этот случай и не представляет сейчас интереса, что порог i₀/C из уравнения (3.5.7) так и не будет достигнут, и клетка все время остается в невозбужденном состоянии. В противном случае она разряжается точно в момент появления какого-то импульса, так что обеспечивается синхронизация. При выборе этого момента в качестве начала отсчета времени величина правой части уравнения (3.5.7) при t = (k- 1) Р + О равна

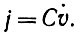(3.5.8)

Следовательно, разряд будет возникать в этот момент времени в том и только том случае, если k - наименьшее целое число, для которого справедливо следующее неравенство:

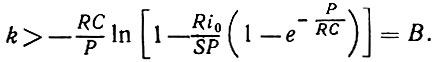(3.5.9)

Другими словами, разряд возникает при t = [B]P.

Теорема 3.5.1. Входная последовательность, состоящая из пиков величины SP, порождает периодический разряд с периодом

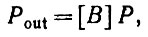(3.5.10)

так что деление частоты происходит со скоростью [5].

Если, в частности, входные импульсы -"быстрые", т. е. подаются с высокой частотой ω_in = 1/I гц, то B в выражении (3.5.9) можно аппроксимировать и получить после некоторых преобразований непосредственное следствие.

Следствие 3.5.1.Ответ будет иметь частоту ω_out, такую, что в пределе

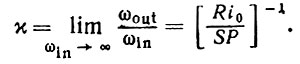
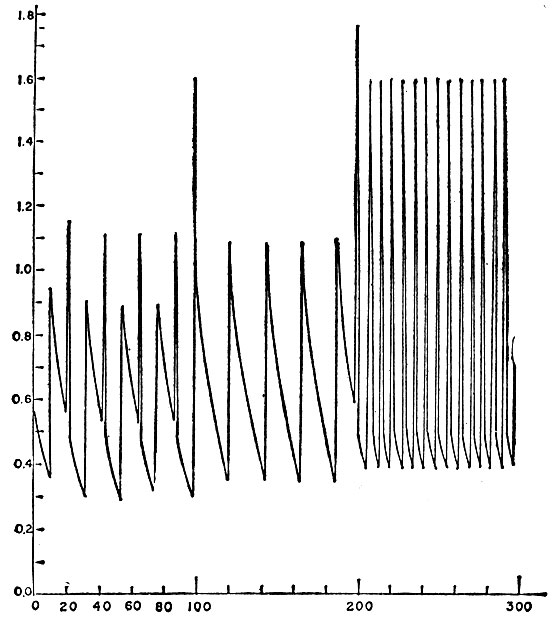
Рис. 3.5.2 а

Соотношение (3.5.11) определяет скорость изменения частоты χ. Если амплитуда пика SP мала, то скобками, выделяющими в (3.5.11) целую часть, можно пренебречь. Мы будем рассматривать здесь только этот случай, поскольку хотим избежать ситуаций, когда выходные импульсы нерегулярны. Постоянная T_{разряда} = RC > (SP⋅C/i₀), и, следовательно, х < 1.

Если форма импульса не соответствует чистой δ-функции, как выше, то разряды необязательно происходят в момент подачи на вход импульсов и синхронизация необязательно имеет место. Процесс может быть достаточно сложным и не сводится просто к делению частоты. Пусть, например, разряд нервной клетки только что произошел и, следовательно, напряжение упало до величины υ₀ - i₀/c. Если, однако, импульс широкий, то его остаточной части может оказаться достаточно для того, чтобы поднять напряжение выше или непосредственно до критического уровня почти немедленно. Если это происходит, выходной сигнал может оказаться совершенно хаотическим, несмотря на простоту приведенной на рис. 3.5.1 схемы. Рис. 3.5.2 и 3.5.3 иллюстрируют ту ситуацию, когда входные импульсы характеризуются частотой, меняющейся во времени сначала медленно, а затем быстро. Графики на рис. 3.5.2а и 3.5.3а представляют результирующее напряжение, а на рис. 3.5.26 и 3.5.36 изображены импульсы тока, возникающие при разряде.

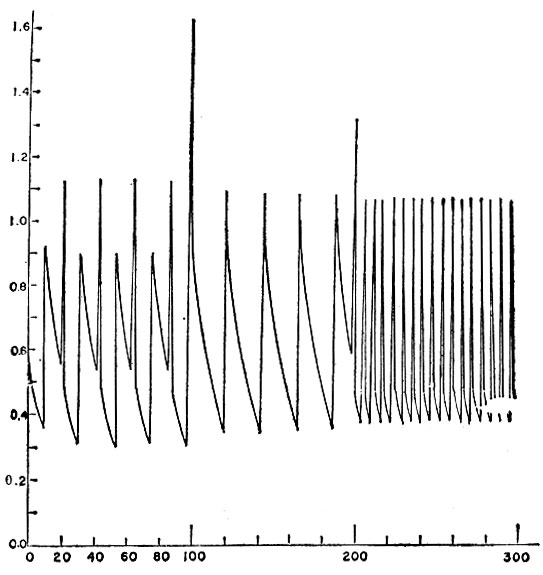
Рис. 3.5.3 а

Приведенный частный случай (широкие импульсы) свидетельствует о том, что выходной сигнал необязательно должен состоять из эквидистантных пиков. Действительно, основной части входного импульса может соответствовать несколько разрядов, за которыми следует состояние покоя, затем новая вспышка и т. д. Выходной сигнал в результате будет состоять из эквидистантных кластеров, каждый из которых включает одно и то же число разрядов. На рис. 3.5.4 приведены результаты решения, полученного на ЭВМ: в данном случае кластеры содержат по четыре пика.

При низкой входной частоте также может возникнуть определенная нерегулярность в выходном сигнале. Читатель, знакомый с генераторами псевдослучайных чисел, основанными на принципе конгруэнтности, обнаружит сходство с эргодическими потоками. Именно поэтому такое простое детерминированное устройство может давать выходной сигнал, который выглядит как случайный.

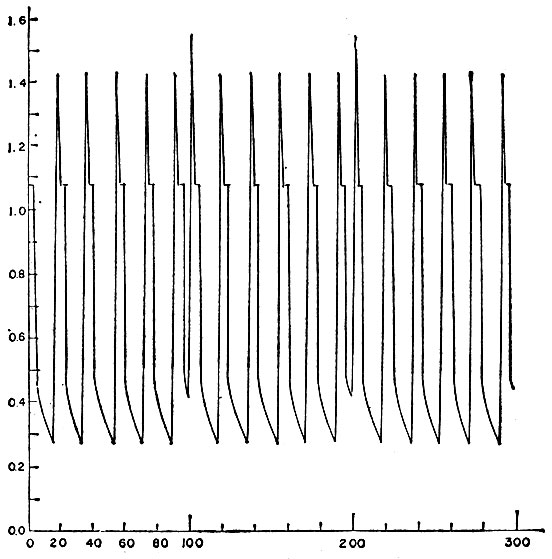
Рис. 3.5.4 а

Если последовательность входных импульсов состоит из периодических импульсов формы P_sh, следующих с частотой ω_in, причем эти импульсы необязательно имеют форму δ-функции, то можно записать следующее:

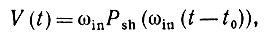(3.5.12)

где t₀ - фаза, а смысл коэффициента ω_in, на который умножается P_sh, заключается в том, что каждый импульс нормирован на одну и ту же площадь независимо от частоты. Затем следует решить уравнение (3.5.7) относительно Т для случая, когда ω_in принимает большие значения, и мы сделаем это асимптотически.

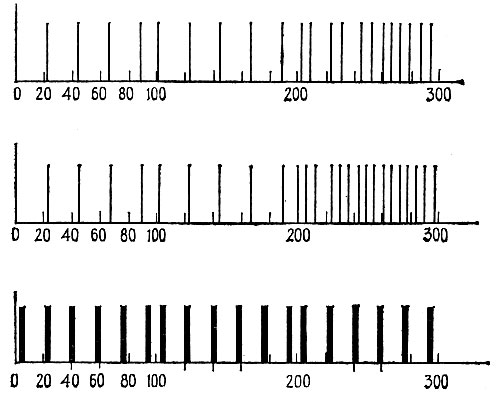
Рис. 3.5.2 б, 3.5.3 б, 3.5.4 б

Положив T = P_out, получаем, что

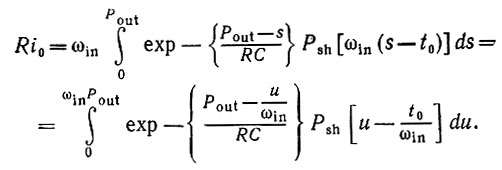(3.5.13)

Для того чтобы выяснить, что происходит при ω_in → ∞ у следует иметь в виду тот очевидный факт, что P_out → 0. Кроме того, показательная функция в диапазоне интегрирования асимптотически равна единице. Следовательно, равенство ω_inP_out = ω_in/ω_out = 1/х должно в пределе удовлетворять следующему уравнению:

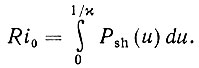(3.5.14)

Таким образом, доказана следующая теорема.

Теорема 3.5.2.Если V(t) - последовательность эквидистантных импульсов формы P_sh, то предельная скорость изменения частоты

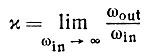(3.5.15)

удовлетворяет уравнению (3.5.14).

Данное утверждение следует сопоставить с (3.5.11). В обоих случаях эту скорость можно выразить через физические постоянные. Мы не настаиваем на всех деталях допущений относительно цепи, приведенной на рис. 3.5.1, но здесь все же необходима нелинейность для того, чтобы получить эффект субгармонического резонанса.