§ 2.2. Некоторые методологические соображения

Детерминированно-статистический подход учитывает, с одной стороны, индивидуальные свойства каждого из элементов учебной выборки, а с другой - интегральные и предельные ее статистические характеристики [2.1].

Детерминированно-статистический подход позволяет почти полностью алгоритмизировать процесс создания опознающего устройства.

Существенной особенностью подхода является то, что наиболее эффективное его применение относится к задачам с достаточно большим алфавитом образов. Эта особенность проявляется как при выборе математических методов обработки информации, так и при разработке функциональных блоков опознающего автомата.

Основными параметрами любого опознающего автомата, каким бы методом он ни создавался, является число ошибок на экзамене и сложность его аппаратурной реализации. (Требования к унификации узлов и простоте аппаратуры становятся особенно важными при создании опознающего автомата для большого алфавита образов.) Естественно считать критериями оптимальности критерии типа минимума вероятности ошибок на экзамене при заданной сложности опознающего устройства или минимума сложности аппаратуры при заданной вероятности ошибок на экзамене.

Создание автомата, удовлетворяющего этим глобальным критериям оптимизации в условиях недостатка априорной информации о структуре распознаваемых образов, в настоящее время практически нереально.

Для упрощения задачи процесс проектирования опознающего автомата (или, другими словами, процесс обучения) разбивается на ряд последовательных этапов, в каждом из которых оптимизируется свой критерий качества.

Согласование критериев качества этапов детерминированно-статистического подхода с глобальным критерием качества опознающего устройства достигается следующим образом.

Все этапы проектирования, за исключением последнего, направлены на упрощение функциональной структуры опознающего автомата при сохранении теоретической возможности построения безошибочного решающего правила. Фактически после каждого из этих этапов требуется сохранение условия ε не пересекаемости образов, которое обеспечивает существование множества безошибочных решающих правил.

Для проверки условия не пересекаемости образов после каждого этапа производится оценка метрической близости образов, т. е. производится оценка фактической величины ε.

Может оказаться, что на различных этапах величина ε измеряется в различных метриках. Важно лишь, чтобы сама величина ε превосходила в несколько раз аппаратурную погрешность в соответствующей метрике. При этом величина ε является своеобразным регулирующим параметром, влияющим на окончательный выбор числа признаков на этапе их выделения или числа исходных параметров - на этапе сокращения размерности исходного описания. Процедура получения оценки меры непересекаемости образов по конечной учебной выборке подробно рассматривается в главе III.

Что касается последнего этапа - этапа построения решающей функции, то отыскание хотя бы одного из безошибочных решающих правил даже при строгом сохранении условия ε не пересекаемости образов возможно только в том случае, если учебная выборка представительна. Очевидно, представительность учебной выборки зависит от ее объема, сложности пространственных конфигураций областей^* и их относительной метрической удаленности. Так как на практике чаще всего объем учебной выборки мал и эффективные непараметрические оценки ее представительности нам неизвестны, то говорить о построении наилучшего решающего правила можно лишь в статистическом смысле, например в смысле минимума вероятности ошибок на экзамене. Поэтому на последнем этапе решается задача минимизации областей альтернативных ошибок опознания при заданном уровне ошибок неправильного опознания и отказа, а также при заданной (т. е. полученной на предыдущих этапах) сложности опознающего автомата.

^* (Областью g-го образа S⁰_q в пространстве X называется множество точек х ∈ X таких, что

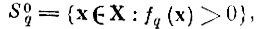
где f_q (х) - многомерная плотность распределения образа q.)

Для оптимизации отдельных этапов проектирования опознающего автомата в излагаемом подходе рассматриваются как статистические, так и детерминированные критерии качества.

Основной причиной использования этих двух различных по духу типов критериев является недостаточный объем априорной информации об образах. Очевидно, что при применении статистических методов получаемые результаты будут тем лучше, чем полнее будут учтены статистические свойства образов. Наиболее полная информация об образах заключена в их многомерных распределениях. Однако в большинстве практических задач опознания эти распределения априорно неизвестны и не могут быть получены с удовлетворительной точностью из-за явного несоответствия объема учебной выборки и размерности пространства исходного описания.

Поэтому для выделения полезной с точки зрения опознания информации практически можно использовать лишь такие статистические критерии, которые оперируют со статистическими характеристиками, обладающими достаточной устойчивостью при оценке их по реальной учебной выборке. К таким характеристикам в первую очередь относятся первые и вторые моменты, которые описывают статистические свойства основной массы реализаций образов. Однако такое описание является слишком грубым приближением. Для более полного описания свойств образов дополнительно привлекаются детерминистские критерии, которые используют информацию о всех и о каждом в отдельности членах выборки и в некоторой степени компенсируют отсутствие информации о статистических моментах высших порядков.

В основном детерминированные методы используются на этапе нахождения решающего правила. Здесь каждая реализация учебной выборки рассматривается как представитель некоторого подмножества реализаций будущей экзаменационной выборки, группирующегося в окрестности данной реализации.

Поскольку плотность распределения в любой данной точке неизвестна, то при применении детерминированных методов возникают трудности, связанные с прогнозом поведения опознающего автомата на экзамене. Для решения этого вопроса опять привлекаются статистические критерии. На этот раз эти критерии оперируют некоторыми одномерными экстремальными статистическими характеристиками, для получения которых в случае большого алфавита образов и при некоторых не жестких дополнительных условиях объем выборки на класс может быть относительно небольшим.

С помощью такой независимой контрольной выборки можно не только произвести оценку качества решающего правила, сформированного на учебной выборке, но и откорректировать решающее правило так, чтобы обеспечить требуемое соотношение различных типов ошибок (см. главу VII).

Таким образом, при выделении полезной для опознания информации детерминированные критерии дополняют результаты интегральных (усредняющих) статистических критериев, а одномерные экстремальные статистические параметры позволяют придать детерминированным критериям экстраполирующие свойства.

Перечислим основные этапы детерминировано-статистического подхода:

1) выбор исходного описания и устранение явных неинвариантностей в исходном описании образов;

2) создание системы признаков;

3) сокращение размерности пространства исходного описания образов;

4) нахождение решающего правила;

5) коррекция решающего правила и прогноз поведения опознающего автомата.