Некоторые математические проблемы, связанные с процессом роста фигур. Станислав Улам
1. Введение. В этой статье содержится краткое описание определенных свойств фигур, получающихся в двумерном и трехмерном пространствах при помощи довольно простых рекурсивных соотношений. Начав с исходной конфигурации, определим последовательные "поколения", которые присоединяются к существующей фигуре; это и представляет собой, так сказать, рост начальной модели в дискретные моменты времени. "Средой" для роста будет плоскость (или пространство), разбитая на одинаковые элементарные фигуры. Например, плоскость можно разбить на квадраты, или на равносторонние треугольники (а пространство можно разбить на кубы и т. д.). Начальная конфигурация будет представлять собой конечное число элементов такого разбиения, и мы зададим индуктивное правило, определяющее последовательные приросты к исходной конфигурации.
Простейшие наблюдаемые структуры, например в кристаллах, периодичны, и их свойства подвергаются интенсивному математическому изучению. Правила, которые мы будем применять, приведут к значительно более сложным и, вообще говоря, непериодическим структурам, установить свойства которых, несмотря на относительную простоту применяемых нами рекурсивных соотношений, весьма трудно. Кажется, что определенные таким образом структуры являются, так сказать, промежуточными по сложности между неорганическими структурами (такими, как кристаллы) и значительно более сложными органическими молекулами и структурами. На самом деле одна из целей данной статьи состоит еще и в том, чтобы на примерах (хотя и заведомо несколько искусственных) продемонстрировать огромное разнообразие объектов, которые можно получить посредством довольно простых индуктивных определений. Кроме того, при этом еще можно получить побочные сведения, проливающие свет на вопрос о том, сколько "информации" необходимо для описания структур живых организмов, имеющих на вид чрезвычайно сложное строение.
Значительная часть нашей работы выполнялась совместно с доктором Дж. Холладеем [1] и Робертом Шрандтом [2]. Для того чтобы получить большое число таких структур и проследить (как во времени, так и в пространстве) определенные свойства их морфологии, мы пользовались вычислительной машиной Лос-Аламос-ской научной лаборатории. Большинство полученных результатов по самой своей природе эмпирические, и для таких структур до сих пор удается теоретически установить лишь очень небольшое число свойств.
2. Простейший случай разбиения - это разбиение бесконечной плоскости на квадраты. Начнем с первого поколения, состоящего из конечного числа квадратов, и определим правило роста следующим образом. Пусть имеется заданное число квадратов n-го поколения; квадратами (n+1)-го поколения будут квадраты, смежные (т. е. имеющие общие стороны) с одним и только одним квадратом n-го поколения. Например, если первое поколение состоит из одного квадрата, то, используя это правило, получаем картину для пяти поколений, приведенную на рис. 1.

Рис. 1
Очевидно, что при таком правиле роста фигура будет продолжать увеличиваться до бесконечности. Она будет обладать исходной симметрией начальной конфигурации (одного квадрата), и все квадраты, расположенные на четырех взаимно перпендикулярных осях, будут принадлежать фигуре, представляющей собой "стволы" и растущие в сторону от них ветви различной длины.
Можно сразу же рассмотреть слегка измененное правило роста. Начнем, как и ранее, с одного квадрата и определим (n+1)-е поколение как квадраты, смежные с квадратами n-го поколения, но так, чтобы никакие два квадрата (n+1)-го поколения ни в одной точке не касались друг друга. На рис. 2 показаны пять поколений, полученных по второму правилу*. Легко видеть, что теперь "стволы" будут неограниченно расти, а плотность появляющихся квадратов будет меньше, чем в предыдущем случае. В обоих случаях можно рассчитать, какие квадраты будут принадлежать фигуре и какие нет.
* (На самом деле автор разрешает появляться тем квадратам (n+1)-го поколения, которые имеют общую вершину, если они происходят от одного родителя. См. пример 2 в конце статьи.- Прим. ред.)
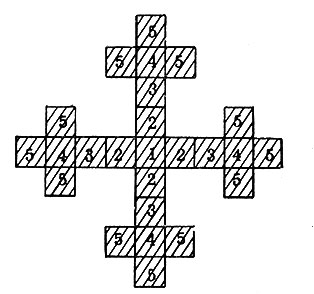
Рис. 2
Системы, растущие по этим двум правилам (и даже несколько более общие системы), обладают общим свойством, которое выражается следующей теоремой, принадлежащей Дж. Холладею. Для поколения, номер которого n представим в виде n = 2h, рост прекращается по всем направлениям, за исключением "стволов", т. е. прямых линий, выходящих из исходной точки роста. Старые боковые ветви прекращают свой рост, и из стволов начинают расти только новые ветви.
Одна из наиболее интересных ситуаций возникает, когда в плоскости, разбитой на равносторонние треугольники, из одного треугольника начинает расти фигура, порождающая поколение за поколением. И в этом случае можно рассмотреть правило, аналогичное вышеприведенному первому правилу для квадратов, т. е. в качестве (n+1)-го поколения взять все треугольники, смежные с треугольниками n-го поколения, за исключением треугольников, имеющих двух родителей в n-м поколении. Система, которая при этом вырастет, будет обладать симметрией исходной фигуры (т. е. гексагональной симметрией). Плотность треугольников, принадлежащих растущей фигуре, будет довольно высокой. Второй вариант правила роста - взять в качестве "правила исключения" аналог второго правила для случая квадратов, т. е. не причислять к (n+1)-му поколению треугольник, если он может хотя бы в одной точке коснуться другого потенциального потомка некоторого элемента из n-го поколения. (Мы, конечно, разрешаем двум потенциальным потомкам касаться друг друга своими вершинами, если они происходят от одного родителя.) Это правило ведет к структуре, которая имеет меньше элементов и, следовательно, меньшую их плотность на плоскости, чем структура, возникающая при росте по первому правилу.
Можно легко доказать, что растущая фигура будет наследовать гексагональную симметрию исходной фигуры и что рост будет продолжаться бесконечно, ибо стволы, увеличиваясь в каждом поколении на один элемент, образуют непрерывные линии. Отростки от ствола имеют различную длину, и их рост прекращается в разные моменты времени (т. е. элементы на концах отростков принадлежат разным поколениям). Автору не удалось доказать, что будут существовать неограниченно длинные ветви. Можно показать, однако, что будут ветви любой произвольной, наперед заданной длины. На рис. 7 изображен сегмент структуры, образовавшейся при росте по рассмотренному только что правилу. Этот сегмент представляет собой половину шестидесятиградусной секции; другая половина получается путем зеркального отражения. Остальные секции получаются путем поворота рассмотренной секции на 60°.
При росте треугольников по первому правилу сохраняется свойство системы, выраженное теоремой Холладея: отростки прекращают свой рост в поколении, номер которого n представим в виде n = 2h. Однако если рост фигуры подчиняется второму правилу, то не только нельзя определить асимптотическое значение плотности треугольников, занятых растущей фигурой (плотности по отношению ко всем треугольникам плоскости), но не удается даже установить сам факт существования такой предельной плотности.
Разбив плоскость на правильные шестиугольники и начав, скажем, с одного элемента, можно получить аналоги двух описанных выше моделей. И здесь при первом правиле у отростков будет происходить прекращение роста в определенном поколении, а для более жестко ограничивающего второго правила, так же как и раньше, невозможно предсказать какие-либо асимптотические свойства растущей фигуры.
3. Образование элемента (n+1)-го поколения осуществляется одним родителем: каждый элемент "в одиночку" пытается породить новый элемент следующего поколения. Однако сам факт разбиения плоскости на квадраты, треугольники, шестиугольники и т. п. допускает несколько возможных интерпретаций: так, скажем, в случае разбиения плоскости на треугольники за элемент разбиения можно принять не площадь треугольника, а вершины треугольников, при этом пара вершин n-го поколения порождает одну вершину (n+1)-го поколения, а именно ту, которая с первыми двумя образует треугольник. Фактически идея рассмотреть это построение новых элементов возникла из следующих соображений.
В статье [3] рассмотрена задача о системе с "бинарной" реакцией. Математический аспект ситуации, возникающей в таких системах, таков: дано большое число элементов, каждый из которых может принадлежать, скажем, к одному из трех типов. Эти элементы соединяются в пары и образуют в следующем поколении другую пару элементов, тип которой определяется однозначной функцией от типов двух родителей. Задача состоит в том, чтобы уметь определять свойства состава таких популяций в разные моменты времени. Если через х, y, z обозначены доли трех типов элементов в n-м поколении, то ожидаемое число частиц каждого типа в новом поколении задается квадратичным преобразованием. Например, правило может состоять в том, что частицы типа х и типа у вместе образуют частицу типа х, (х + х) дает частицу типа z, (x + z) - частицу типа y, (y + y) - частицу типа х, (y + z) - частицу типа z и, наконец, (z + z) дает частицу типа y. (В действительности существует более чем девяносто возможных и различных правил такого типа; мы предполагаем, однако, что одно правило действует в течение всего времени.) Наше правило приводит к следующим выражениям для новых долей х', y', z':
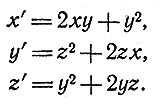
Это не что иное, как преобразование части плоскости в себя. Мы имеем три переменных, связанных между собой соотношениями x + y + z = 1 = x' + y' + z'. Повторное применение этого преобразования дает ожидаемое число элементов каждого типа в последовательных поколениях. В работе [3] были установлены некоторые свойства итераций таких преобразований. В частности, в некоторых случаях итерации могут сходиться к устойчивому распределению, а в других - имеет место сходимость к осциллирующему распределению и т. д.
В указанной работе рассмотрено случайное соединение (или столкновение) двух элементов. Естественно возникает вопрос о поведении таких систем в случае, когда взаимодействие двух элементов подчинено неслучайному закону, а некоторым ограничениям, вытекающим, скажем, из геометрии. Например, наиболее строгое ограничение, которое, как нам кажется, можно себе представить, состоит в том, что элементы представляют собой вершины разбиения плоскости на равносторонние треугольники, причем каждая вершина окрашена в один из трех цветов. Рассмотрим заданную исходную конфигурацию и допустим, что новый элемент образуется парой вершин, расположенных на одной стороне какого-либо треугольника. В простейшем случае можно начать с одного треугольника, все три вершины которого окрашены в разные цвета (т. е. относятся к различным типам). Затем тремя парами вершин, расположенными по трем сторонам данного треугольника, образуем новые вершины, являющиеся следующим поколением; цвет каждой из новых вершин будет функцией от двух цветов его родителей. Получим тогда второе поколение и продолжим далее таким же образом. Однако мы немедленно обнаружим, что такое построение нельзя провести единственным образом, ибо уже для небольшого числа поколений появятся две пары вершин, расположенные таким образом, что потомком каждой из них должна стать одна и та же вершина. Какой цвет следует приписать новой вершине? Может ведь случиться, что две родительские пары предпишут новой точке два различных цвета.
Один из возможных выходов из такой ситуации состоит в том, чтобы не рассматривать точку, для которой могут возникнуть два взаимоисключающих правила определения цвета, а считать, что такая вершина останется незанятой. Распространение этого правила на точки, в которых вследствие соприкосновения двух ранее построенных треугольников получается неоднозначное определение цвета, и привело к работе, упомянутой в предыдущих абзацах. Структуры, упоминавшиеся выше, действительно можно рассматривать как состоящие из точек трех различных типов (вообразим, например, что новые точки являются молекулами, образовавшимися в результате двойной связи, и т. д.). Однако, как это было замечено Шрандтом и автором, возможны и другие правила для определения цвета в тех точках, где две пары родителей дают взаимопротиворечащие правила определения цвета. Одно правило (1) предусматривает выбор такого типа, который не принадлежит ни к одному из двух, получающихся при неоднозначном определении. Поскольку существуют три типа, то если два правила определения новой точки дают два различных типа, можно выбрать третий тип. Было рассмотрено также и другое правило (2): выбрать один из двух типов случайно, с вероятностью 1/2 для каждого из них. Еще одно правило (3) заключается в том, что в случае противоречия выбирается четвертый цвет, доля которого обозначается через w, причем тип w с типом x дает тип x, y + w образует y, z + w образует z и, наконец, случай w + w приводит снова к типу w. Четвертый тип можно интерпретировать как молекулу такого типа, которая может воспроизводиться лишь при взаимодействии с молекулой своего типа. Поведение таких систем было изучено экспериментально с помощью вычислительной машины. Правило (2), при котором тип точки иногда определяется случайно, отчасти перекликается с работой [3], где рассматривается случайное соединение. Возможно, что при всех этих правилах существует сходимость числа частиц различных типов к устойчивому распределению (в противоположность поведению при итеративном применении квадратичного преобразования, где во многих случаях существует осциллирующий предел или еще более нерегулярное эргодическое асимптотическое поведение). В некоторых случаях, вероятно, имеет место сходимость к фиксированной точке (т. е. к определенным значениям x, y, z), а в случае правила (2) - сходимость к величине, численно не слишком отличающейся от фиксированной точки соответствующего квадратичного преобразования. Доказать существование предельного распределения не удалось, хотя численные расчеты четко указывают на его существование. Следует заметить, что все исходные конфигурации принадлежали к наиболее простому из возможных типов, т. е. состояли из одного триплета точек.
4. Вернемся теперь к обсуждению картины роста фигуры, в которой каждому новому элементу не приписывается никакого цвета, и будем просто рассматривать геометрию растущей фигуры, как это делалось во втором пункте. При этом возникает задача о свойствах роста таких фигур при наличии правила стирания или "смерти" старых элементов: предположим, мы зафиксировали произвольно выбранное целое k и наше рекурсивное определение построения новых элементов включает в себя правило, согласно которому мы стираем с картины все элементы, прожившие в течение k поколений. В частности, положив k = 3, выберем в качестве начальной конфигурации квадрат и рассмотрим рост, подчиняющийся первому правилу п. 2 при дополнительном условии, что после построения (n+1)-го поколения мы сотрем все точки (n-1)-го поколения. (Это позволяет конфигурации расти в обратную сторону, занимая точки, ранее принадлежавшие поколениям с индексом l, меньшим чем n-1.) При таком построении, начав, скажем, с двух квадратов, можно наблюдать рост картины, которая через некоторое время разделится (вследствие стирания), а позднее снова восстановится. Были предприняты поиски такой исходной конфигурации, которая в последующих поколениях разделится, образуя фигуры, сходные или идентичные исходной, т. е. воспроизведется хотя бы в некоторых поколениях. Вообще говоря, даже в случае без стирания, когда картину роста можно предсказать, невозможно описать вид фигур, двигающихся весьма хаотично. Однако в случае одной исходной конфигурации можно предсказать будущее поведение. Эта конфигурация состоит из двух квадратов, касающихся друг друга в одной точке и расположенных по диагонали. При росте по правилу (1) и со стиранием клеток, возраст которых равен трем, такая конфигурация в каждом 2p поколении (p = 1, 2, 3, ...) воспроизведет по крайней мере четыре свои копии, смещенные на 2p ячеек от исходной конфигурации. Такое же поведение будет и у исходной модели, состоящей, скажем, из 4 квадратов, расположенных по диагонали, из 8, 16 и т. д.
Экспериментально было изучено также поведение фигуры, растущей в плоскости, разбитой на треугольники, при наличии условия стирания старых элементов. Процесс роста в этом случае можно описать следующим образом: задано конечное число вершин в плоскости, разбитой на треугольники (некоторым из них присвоен индекс (n-1), другим n); вершинам треугольников, стороны которых имеют индексы либо (n-1) и n, либо n и n, присваивается индекс (n+1); здесь снова точки с неоднозначным определением не причисляются к (n+1)-му поколению. Далее все точки с индексом (n-1) стираются. Наше правило в случае разбиения плоскости на квадраты для любой нетривиальной начальной конфигурации позволяет растущей фигуре существовать неограниченно долго. Однако в случае разбиения плоскости на треугольники так бывает не всегда. В частности, начальная конфигурация, состоящая из двух вершин, принадлежащих одному поколению, прекращает рост после десятого поколения; другими словами, все точки, которые могли бы стать одиннадцатым поколением, являются точками с двузначным определением, и поэтому, согласно нашему правилу, рост прекращается. Здесь следует указать, что в случае, когда имеется правило "смерти", по которому все элементы возраста k стираются, надо обязательно определить, какие элементы исходной конфигурации принадлежат к 1-му, а какие ко 2-му поколению, ибо, например, две вершины, одна из которых принадлежит к 1-му, а другая ко 2-му поколению, образуют жизнеспособную конфигурацию.
5. Аналогичное экспериментальное изучение роста конфигурации было выполнено в трехмерном пространстве для случая кубической решетки. Здесь также можно рассмотреть правила роста, аналогичные правилам для двумерного случая. Начав с одного куба, можно построить новые кубы, принадлежащие растущей фигуре,- это кубы, смежные с кубами предыдущего поколения (т. е. имеющие с ними общие грани). К числу новых кубов снова не следует относить те, которые имеют более чем одну общую грань с кубами предыдущего поколения. Аналог первого правила дает систему, плотность которой в пространстве стремится к нулю. Это отличается от ситуации в плоскости, где в этом случае достигается положительная плотность.
Рост трехмерной системы при наличии правила стирания старых элементов был исследован на вычислительной машине Р. Шрандтом. Ниже кратко описан случай, когда стираются элементы, существовавшие в течение трех поколений. Создается впечатление, что картина роста характеризуется наличием плоских гроздьев, составленных из кубов. Эти гроздья связаны тонкими цепочками.
Такое эвристическое изучение уже в двумерном случае показывает, что многообразие структур роста слишком велико, чтобы его можно было просто охарактеризовать.
Автор попытался ввести соответствующие определения для одномерного случая, надеясь, что при этом удастся обнаружить некоторые общие свойства последовательностей, определенных при помощи рекурсивных правил, аналогичных правилам двумерного случая. Предположим, что мы следующим образом определяем последовательность целых чисел: начав с чисел 1 и 2, строим последовательность, каждый член которой равен сумме каких-нибудь двух предыдущих, но не включаем те суммы, которые можно получить более чем одним способом. При этом мы никогда не будем складывать числа сами с собой. Получим следующую последовательность: 1, 2, 3, 4, 6, 8, И, 13, 16, 18, 26, 28,... . Число 5 не включено в последовательность, ибо его можно получить как сумму предыдущих членов двумя различными способами. Следующее целое число, которое можно представить одним и только одним способом как сумму предыдущих членов,- это число 6; 7 можно представить двумя способами, но 8 представимо лишь единственным способом. Следующее такое число есть 11 и т. д. Начав с 1 и 3, получим последовательность 1, 3, 4, 5, 6, 8, 10, 12, 17, 21, .... По мнению автора, даже здесь, к сожалению, не легко установить свойства таких "последовательностей однозначно определенных сумм". Например, трудно ответить на вопрос о том, существует ли бесконечно много близнецов, т. е. целых чисел, принадлежащих последовательности и отличающихся друг от друга на число 2. Не легко дать и хорошую оценку плотности такой последовательности по отношению к множеству всех целых чисел.
Цель, которую преследовало опубликование этих разрозненных экспериментальных работ, заключается в том, чтобы указать на задачи, связанные с комбинаторикой систем, которые чрезвычайно упрощенным и схематическим образом демонстрируют картину роста, подчиняющегося простым геометрическим условиям. Очевидно, что прежде чем можно будет получить некоторые общие свойства такого "роста", необходимо просмотреть большое количество экспериментальных данных. На вычислительной машине можно изучить влияние многих изменений в наших правилах. Кинескоп, подключенный к машине, позволяет непосредственно наблюдать получающиеся структуры - машина считает их очень быстро. Эти работы продолжаются, и, возможно, будут установлены некоторые более общие свойства морфологии растущих систем.
Приложение: примеры
Пример 1. Первое поколение, с которого начинается рост фигуры, состоит из одного квадрата (на рисунке он окрашен в черный цвет). Каждое последующее поколение состоит из квадратов, смежных с одним и только одним квадратом предыдущего поколения. В большинстве приведенных здесь иллюстраций начерчены лишь ячейки, отвечающие определенному направлению роста. В силу симметрии условий рост по другим направлениям совершенно аналогичный. (См. рис. 3.)

Рис. 3
Пример 2. "Мальтийские кресты". Черные ячейки в этой структуре имеют то же строение, что и в модели примера 1, за исключением того, что они значительно более разбросаны. Здесь используется то же правило, что и в примере 1, но со следующим дополнительным ограничением: если ячейка могла бы соприкоснуться с другой (уже начерченной или той, которая может принадлежать этому же поколению) либо по стороне, либо в вершине, то такая ячейка не возникает. Однако в двух случаях из этого ограничения делается исключение:
- если ячейка касается другой, потому что у них общий родитель;
- в случае, изображаемом схемой
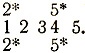
Двум элементам пятого поколения, отмеченным звездочками, разрешено коснуться потенциальных (хотя ранее уже отвергнутых) потомков третьего поколения. Это необходимо сделать для того, чтобы дать возможность роста ветвям, образующим с исходным направлением прямой угол. Заметим, что потомки третьего поколения были отвергнуты только потому, что они могли коснуться потенциальных потомков элементов второго поколения, отмеченных звездочкой. (См. рис. 4.)

Рис. 4
Пример 3. Эта структура построена по тому же правилу, что и структура первого примера, но плоскость разбита на треугольники, а не на квадраты. (См. рис. 5.)
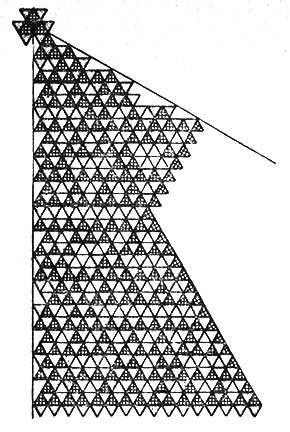
Рис. 5
Пример 4. Эта структура построена по тому же правилу, что и структура примера 3, но с одним исключением: если ячейка может коснуться угла некоторой старой ячейки (но не родительской), то такая ячейка не включается в число элементов структуры. (См. рис. 6.)
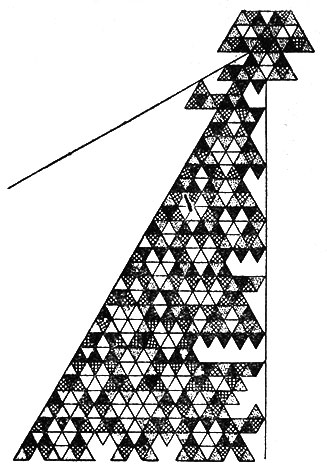
Рис. 6
Пример 5. Эта структура построена по такому же правилу, что и структура в четвертом примере, но с одним исключением: если две новые ячейки (имеющие разных родителей) могут коснуться друг друга хотя бы своими вершинами, то они обе не включаются в число элементов структуры. (См. рис. 7.)

Рис. 7
Пример 6. Эта структура построена по тому же правилу, что и структура примера 1, но плоскость здесь разбита на шестиугольники, а не на квадраты. Причина кажущейся разобщенности частей этой структуры заключается в том, что левее изображенного треугольника из ячеек лежит такой же треугольник. Этот треугольник получается путем зеркального отражения из треугольника, образованного несколькими первыми поколениями. (См. рис. 8.)
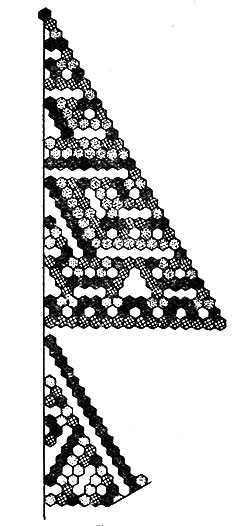
Рис. 8
Литература
- Holladay J. С., Ulam S. M., Notices Amer, Math. Soc, 7 (1960), 234.
- Schrandt R. G., Ulam S. M., Notices Amer. Math. Soc, 7 (1960), 642.
- Stein P. R., Ulam S. M., Quadratic Transformations, Los Alamos Laboratory Report LA-2305, 1959.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'