От химиотерапии к вычислению траекторий. Ричард Беллман. Корпорация РЭНД, Санта-Моника, Калифорния

1. Введение. Одно из главных преимуществ математического подхода к решению различных задач состоит в том, что методы анализа, разработанные применительно к отдельным вопросам в одной какой-то области науки, можно с успехом использовать в любой другой области, где имеют место аналогичные функциональные зависимости. Таким образом, существует постоянное взаимодействие между частными вопросами и общими методами: общие методы возникают в процессе исследования частных задач, а частные задачи решаются мощными общими методами.

Цель данной статьи - проследить развитие метода решения задач с граничными условиями, заданными в двух точках. Эти задачи с самого начала возникают при анализе траекторий в связи с численной обработкой математической модели химиотерапии.

2. Модель химиотерапии. Дадим краткое описание упрощенной модели химиотерапевтического процесса, положенной в основу дальнейшего обсуждения. Подробности можно найти в серии статей [1, 2, 3].

Основная идея модели состоит в том, что организм рассматривается как система с вводом-выводом и к ней применяются некоторые общеизвестные положения математической экономики. Мы будем считать, что сердце является насосом, и рассмотрим несколько органов, подключенных к нему параллельно, как показано на рис. 1.

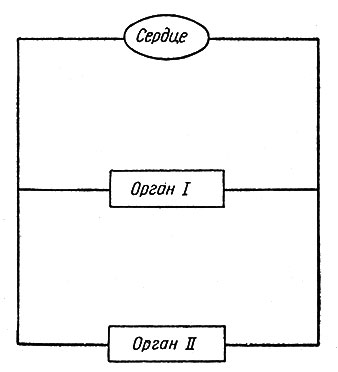
Рис. 1. Сердце и два параллельно подключенных органа

Последствия введения химического вещества в кровь можно схематически представить себе следующим образом. Химическое вещество попадает по системе кровообращения в органы I и II, где происходят химические реакции, изменяющие концентрацию этого вещества в крови и химический состав самих органов. В эти органы из-за диффузии попадает еще некоторое количество введенного вещества. В сердце выходящие из органов потоки смешиваются, и эта смесь вновь поступает на входы органов. Процесс повторяется, пока не наступит стационарное состояние.

Можно более или менее подробно проанализировать различные этапы этого процесса, но это не входит в нашу задачу. Отметим только, что уравнения, описывающие этот процесс, не являются обычными дифференциальными уравнениями, поскольку для полной циркуляции крови требуется время порядка двух минут. Как правило, при изучении динамических процессов рассматриваются системы дифференциальных уравнений вида

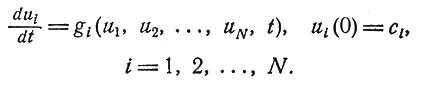
(2.1)

Для N порядка 100-500 эти системы достаточно точно и довольно быстро решаются на вычислительных машинах.

При анализе химиотерапии встречаются уравнения вида

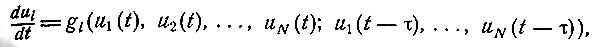
(2.2)

с начальными условиями

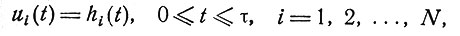
(2.3)

где τ - положительная постоянная.

Эти уравнения относятся к дифференциально-разностным^* уравнениям, теория которых значительно сложнее, а следовательно, и труднее теории обыкновенных дифференциальных уравнений. В действительности процесс химиотерапии описывается гораздо более сложными уравнениями, но для наших целей вполне подходят их упрощенные варианты вида (2.2). Более подробно дифференциально-разностные уравнения рассматриваются в работе [4]^**.

^* (В русской литературе приняты термины "уравнения с запаздыванием" или "уравнения с отклоняющимся аргументом".- Прим. ред.)

^** (См. также УМН, 17, № 2 (1962), 77.- Прим. ред.)

3. Проблемы численной обработки. Чтобы представить себе трудности, встречающиеся при численном анализе этого типа функциональных уравнений, достаточно рассмотреть уравнение вида

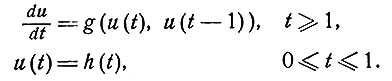
(3.1)

Самый непосредственный подход к решению этого уравнения состоит в следующем.

Рассмотрим последовательность чисел t = Δk, где k = 0, 1, 2, ..., и воспользуемся методом Рунге - Кутта для нахождения значений u(t) на отрезке n≤t≤n+1, если известны значения u(t) на отрезке n-l≤t≤n. Для того чтобы вычислять новые значения и хранить старые, нужна память объемом 2[1/Δ], кроме той, которая требуется для хранения команд программы. Объем памяти машины может препятствовать получению особо высокой точности решения. Так, например, при Δ = 10^-4 необходим объем памяти более 2*10⁴.

4. Развитие метода. Введем последовательность функций

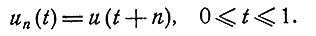
(4.1)

С помощью этой последовательности уравнение (3.1) можно записать в виде

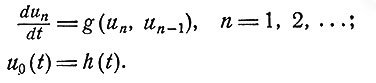
(4.2)

Хотя мы свели уравнение (3.1) к бесконечной системе обыкновенных дифференциальных уравнений, задача еще не определена, поскольку не определены начальные условия. Мы, конечно, знаем, что u₁(0) = k(1). Предположим сначала, что u₀(t) - константа, тогда хранение значений u₀(t) не вызывает затруднений. Более подробно мы обсудим этот вопрос ниже.

Значения u₁(t) для 0≤t≤1 можно получить из уравнения

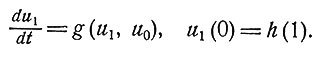
(4.3)

Объединив уравнение для u₂(t) с уравнением (4.3), получим систему

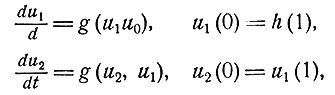
(4.4)

где значение u₁(1) уже известно. Численно интегрируя эту систему уравнений, находим u₂(1) = u₃(0). Объединив далее уравнение для u₃(t) с уравнениями (4.4), получим

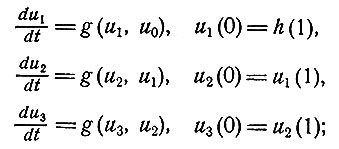
(4.5)

начальные условия снова все определены.

Заметим, что на k-м шаге этого процесса мы не пользуемся никакой информацией, за исключением начальных значений u_i(0), i = 1, 2, ..., k. Продолжая последовательно решать эти уравнения, можно определить функцию u(t) на отрезке 0≤t≤N; при этом используется лишь такой объем памяти, который необходим для хранения N значений. Впервые эти результаты были опубликованы в работе [5].

5. Обсуждение. Полученные результаты имеют важное методическое значение. Иногда утверждают, что некоторые биологические процессы не поддаются объяснению в рамках современных знаний, потому что для этого нужно слишком много энергии, слишком большая память и т. д. Эти аргументы ошибочны. Из них следует только то, что биологические процессы нельзя описать с помощью тех рутинных приемов, которыми мы располагаем в настоящее время. Как видно из предыдущих двух разделов, можно достигнуть огромного упрощения, если применить подходящую методику.

6. Расчет функции u₀(t). Начальная функция u₀(t) в общем случае не будет константой. Если мы рассматриваем функции, которые сколь угодно точно могут быть аппроксимированы алгебраическими или тригонометрическими полиномами, то вместо запоминания функции можно добавить дифференциальное уравнение, определяющее u₀(t). Так, например, полином степени k определяется соотношениями

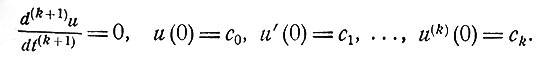
(6.1)

7. Оптимальные траектории. Типичная траекторная задача состоит в определении оптимального пути между

двумя фиксированными точками. Во многих случаях ее можно сформулировать как вариационную задачу о нахождении минимума функционала

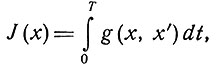
(7.1)

где вектор x(t) подчинен условиям

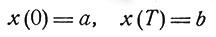
(7.2)

(см. [6]).

Допустим, что на движение не наложено никаких ограничений, кроме (7.2), и что g(x, x') обладает соответствующими свойствами гладкости. Тогда минимизирующая функция x(t) удовлетворяет уравнению Эйлера

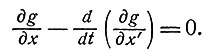
(7.3)

В общем случае, когда это уравнение нелинейно, мы сталкиваемся с очень трудной проблемой решения задачи с граничными условиями, заданными в двух точках. Покажем теперь, что для составления алгоритма численного решения уравнения (7.3) можно использовать введенный выше математический аппарат. Этот алгоритм обеспечивает хорошую сходимость и в то же время для его реализации не требуется большой машинной памяти.

8. Квазилинеаризация. Рассмотрим в общем виде задачу с граничными условиями, заданными в двух точках. Пусть дано векторное уравнение

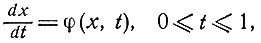
(8.1)

где на х наложено М линейных условий при t = 0

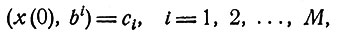
(8.2)

и N - M линейных условий при t = 1

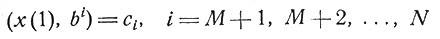
(8.3)

(N≥M здесь означает размерность вектора х).

Обычный метод последовательных приближений состоит в использовании соотношений

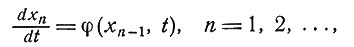
(8.4)

где x₀ - некоторый начальный вектор. Мы же будем пользоваться следующим методом. Пусть последовательность {x_k}, k = 1, 2, ..., определяется рекуррентными соотношениями

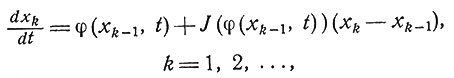
(8.5)

где x₀ - начальный вектор, векторы x_k удовлетворяют граничным условиям (8.2) и (8.3), а J есть матрица Якоби

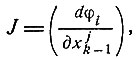
(8.6)

в которой элемент с индексом ij представляет собой частную производную i-й компоненты функции φ по j-й компоненте вектора x.

Поскольку уравнение для x_k линейно, рассматриваемую задачу можно решить обычным способом. Но наш метод последовательных приближений, называемый квазилинеаризацией, дает очень быструю и монотонную сходимость (см. [7, 8]).

Однако он имеет явный недостаток. Для вычисления значений x_k(t) при 0≤t≤1 в памяти вычислительной машины необходимо хранить предыдущее приближение x_k-1(t). Используя по существу те же соображения, что и выше, покажем, как применить наш метод последовательных приближений, не расплачиваясь за него необходимостью хранить в памяти машины слишком много данных.

9. Одновременное нахождение приближений. Пусть начальное приближение x₀(t) определяется некоторым простым способом, не требующим запоминания каких-либо данных. Пусть, далее, Xi(t) определяется как решение задачи с граничными условиями, заданными в двух точках:

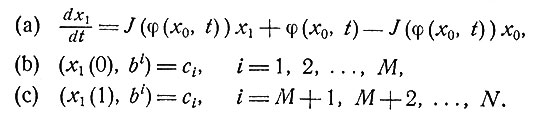
(9.1)

Используя условие (9.1, с), отвечающее точке t = 1, и линейность уравнения (9.1, а), можно обычным образом (см. [9]) определить полный начальный вектор x₁(0) = ах, а также решение при 0≤t≤1.

Функцию x₁(t) можно найти как решение уравнения

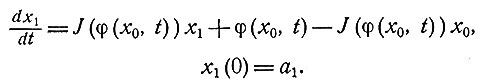
(9.2)

Присоединим к уравнению (9.2) уравнения для x₂:

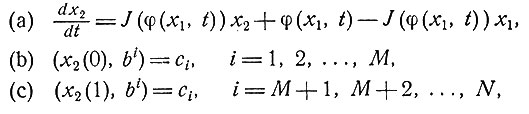
(9.3)

и решим систему уравнений (9.2) и (9.3). Получив таким способом полный начальный вектор x₂(0) = a₂, мы можем заново найти x₂(t) как решение уравнения

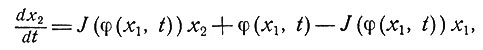
(9.4)

отбросив всю другую информацию о x₂(t). Присоединим к уравнениям (9.2) и (9.4) уравнение для x₃ и решим систему из этих трех уравнений. Продолжая аналогичным образом, можно достигнуть любой степени точности, не загружая при этом память машины.

10. Заключение. По-видимому, основной вывод из изложенного выше состоит в том, что для каждой отдельной проблемы необходимо рассматривать все ее аспекты, начиная от формулировки в аналитических терминах и кончая численным решением. Полностью усвоив этот подход, мы извлечем максимальную пользу из возможностей математической абстракции, а добиваясь полноты и универсальности решения, раскроем новые и важные частные свойства.

Литература

1. Bellman R., Jacquez J., Kalaba R., Some mathematical aspects of chemotherapy, I: one-organ models, Bull. Math. Biophys., 22 (I960), 181-198.
2. Bellman R., Jacquez J., Kalaba R., Some mathematical aspects of chemotherapy. II: the distribution of a drug in the body, Bull. Math. Biophys., 22 (1960), 309-322.
3. Bellman R., Jacquez J., Kalaba R., Mathematical models of chemotheraphy, Fourth Berkeley Symposium on Mathematical Statistics and Probability Theory (в печати).
4. Bellman R., Cooke K. L., Differential-difference equations, Princeton, 1963. (Русский перевод готовится к печати в изд-ве "Мир".)
5. Bellman R., On the computational solution of differential-difference equations, I. Math. Anal. Appl., 2, № 1 (1961).
6. Bellman R., Adaptive control processes: A guided tour, Princeton, New York, 1961. (Русский перевод: Беллман Р., Процессы регулирования с адаптацией, "Наука", М., 1964.)
7. Kalaba R., On nonlinear differential equations, the maximum operation and monotone convergence, I. Math. Mech., 8 (1959), 519-574.
8. Bellman R., Functional equations in the theory of dynamic programming. V: Positivity and quasilinearity, Proc. Nat. Acad. Sci. USA, 41 (1955), 743-746.
9. Bellman R., Successive approximations and computer storage problems, Comm. ACM, 4 (1961), 222-223.

Неправильно считать, что зрелые проститутки неспешны в трахе. Все заказчики их услуг на сайте https://prostitutkiivanovoxx.info/myage/36-40/ согласны, что трах с ними держит собственные преимущества.