Диалог четвертый. Компьютер анализирует эндшпиль

- Не совсем понятно, почему из трех стадий шахматной партии особого рассмотрения удостоилась только заключительная, к тому же не сильнейшая для компьютера.

- Да, но разговор у нас пойдет не об игровых программах, а о специальных, предназначенных для разыгрывания тех или иных классов окончаний.

- Какую практическую ценность они имеют, ведь все равно для игры машине придется пользоваться обычной программой.

- Не совсем так. Для определенных видов эндшпиля в компьютере может быть предусмотрена особая подпрограмма, к которой он обратится в случае необходимости. В результате машина значительно усилит свою игру. Между прочим, в современных моделях шахматных автоматов имеются разъемы для подключения блоков с более мощными программами, в том числе для игры в окончаниях.

- А насколько совершенны специальные эндшпильные программы?

- Сейчас станет ясно, почему данной теме посвящен целый диалог. Дело в том, что в разыгрывании некоторых классов окончаний, в основном малофигурных, машина уже сейчас превосходит человека и с ее помощью можно получить важные, порой весьма неожиданные результаты. А иногда (в этом мы убедимся ниже) компьютер способен произвести самую настоящую сенсацию!

- Вы меня заинтриговали, но сначала поясните, почему обычная игровая программа так сильно уступает специальной эндшпильной.

- Для этого рассмотрим один занятный пример, придуманный Г. Берлинером (рис. 40).

Рис. 40

Интересная позиция?

- Вы меня обижаете. Тут и делать нечего, эксперимент для начинающих. Белый король отправляется на ферзевый фланг, забирает пешку d6, и на этом все кончается. А что же компьютер?

- Для того чтобы обнаружить этот маневр и взять пешку, машине надо перебрать варианты на восемь ходов вперед (16 полуходов), что явно превышает все счетные способности. Не помогает и ФВ: все ходы белого короля просты и относятся к числу "тихих".

- Получается, что, даже случайно блуждая по доске, король (никогда не приблизится к пешке d6. Принцип централизации, заложенный в оценочную функцию, всякий раз заставит его вернуться на вертикаль "d" или "w".

- Именно поэтому Берлинер полагал, что с точки зрения машины, играющей белыми, ничейный исход здесь неизбежен. Я тоже никогда не сомневался в этом и постоянно использовал пример для иллюстрации ограниченных возможностей шахматного автомата. По крайней мере "Экспресс", с которым я сражался дольше всего, владея белыми фигурами, упорно держал короля в самом центре доски. Но вот, предложив как-то эту позицию шахматному компьютеру "Турбостар", я был крайне удивлен, если не сказать поражен, его неожиданной реакцией. Сначала белый король потоптался на месте - 1. Kpd3, 2. Kpe3, 3. Kpd3, а потом уверенно отправился на ферзевый фланг.

- Чем же это объяснить?

- Честно говоря, я и сам не знаю. Ведь информацию о том, какой алгоритм заложен в тот или иной компьютер, какие эвристические методы в нем использованы, авторы редко сообщают в печати. Что касается данного случая, то возможны разные предположения. Первое: то, что в машине содержится специальная программа для разыгрывания пешечных эндшпилей, впрочем, это маловероятно.

- А не думаете ли вы, что при небольшом числе ходов компьютер увеличивает глубину расчета и "вычисляет" решающий маршрут короля?

- Это не исключено, но что-то в прямолинейный перебор вариантов я не верю. Вот более правдоподобная версия. Ходы Kpd3-e3-d3 и т. д. форсируют ничью, а поскольку оценочная функция подсказывает машине, что к мирным переговорам приступать рано, она отказывается от повторения ходов и пробует Kpd3-c3. С учетом централизации значение оценочной функции несколько падает, но остается выгодным для белых, и в переборе машина надеется увеличить его. По тем же причинам на следующем ходу она отказывается от возвращения КрсЗ-d3, а предпочитает Kpc3-b3. Таким образом, в конце концов король добирается до пешки. Перебор оказывается не слишком велик.

- Эти соображения чисто эвристического характера - в другой, родственной позиции предлагаемый метод действий может не дать эффекта.

- Не буду спорить. Но в том, что алгоритм снабжен какой-то необычной эвристикой, сомневаться не приходится. Хотя возможна еще более простая разгадка: в эндшпиле с блокированной пешечной структурой короли, если это не связано с опасностью, стремятся навстречу друг другу. Тогда боковой маршрут белого предводителя тоже не вызывает удивления.

- Все-таки, мне кажется, что при любом алгоритме действий можно придумать позицию, аналогичную конструкции Берлинера: элементарной с точки зрения человека и проблематичной для ЭВМ.

- В принципе это утверждение верно, но оно не относится к специальным программам, в которых предусмотрено рассмотрение всех необходимых ситуаций. Вот мы и подошли к основной теме диалога.

- Не совсем ясно: ведь полный перебор вариантов, то есть изучение всего дерева игры, нереален даже в простейших случаях.

- Ограниченность материала позволяет использовать так называемый ретроспективный анализ (или, кратко, ретроанализ): перебор идет не "вперед", как обычно, а "назад" - от матовых позиций (или позиций, не вызывающих сомнений в оценке) к исходной. Многие ветви дерева при этом отбрасываются, и перебор удается успешно осуществить на компьютере. Кроме того, если некоторая позиция охвачена перебором, то для сильнейшей стороны машина предлагает ходы, приближающие ее к цели, а для слабейшей - оттягивающие ее достижение. Ретроанализ, проведенный для данного класса окончаний, позволяет однозначно оценить каждое из них. Существенно, что полученные оценки уже не могут быть никем оспорены.

- Другими словами, исследование эндшпиля, проведенное с помощью ЭВМ, является исчерпывающим и как бы напоминает математическую теорему.

- Да, но чтобы доказать "шахматную теорему", программистам приходится преодолевать немало технических трудностей, связанных с переработкой большого объема информации. И именно благодаря экспериментам на шахматной модели им удается успешно решать сложные проблемы из области информатики.

- В наших диалогах почти нет строгих математических рассуждений, и мне как будущему математику (а я надеюсь поступить в университет) немного обидно. Может быть, вы более подробно расскажете, что собой представляет ретроспективный анализ?

- Ваше "математическое" замечание вполне законно. Однако думаю, что не всех любителей шахмат волнуют математические нюансы алгоритмов и программ для ЭВМ; некоторых больше интересует конкретный материал: компьютерные комбинации, партии и т. д. Вместе с тем одна из основных задач, стоящих перед нами, заключается в привлечении юных читателей к серьезным занятиям математикой, информатикой, вычислительной техникой. Но если мы попытаемся подробнее углубиться в эти области, то, боюсь, наши диалоги никогда не закончатся...

Что же касается ретроспективного анализа, то я не возражаю: давайте попробуем аккуратно, если хотите, с математической точностью, описать его принципы. (Правда, предупредим читателя, что если ему не очень хочется ломать голову, то пусть пропустит ближайшие несколько страниц.)

Для удобства далее будем рассматривать окончания, в которых белые стремятся к победе, а черные - к ничьей. При изучении данного класса окончаний мы исходим из того, что нам уже известны оценки всех младших эндшпилей, возникающих при любом изменении соотношения сил на доске - взятии фигуры или превращении пешки.

- То есть считается, что анализ, как вы их называете, младших эндшпилей проведен раньше и с ними имеется полная ясность.

- Да, именно так. Теперь введем важное определение. Рангом выигранной для белых (а значит, проигранной для черных) позиции назовем наименьшее число ходов, за которое белые могут объявить мат неприятельскому королю или перейти в выигранный младший эндшпиль (независимо от очереди хода).

- При определении ранга позиции, наверное, предполагается, что обе стороны действуют наилучшим образом?

- Разумеется. В дальнейшем, говоря, что в данном окончании белые выигрывают в n ходов, мы, как правило, подразумеваем, что перед нами позиция n-то ранга.

Опишем теперь алгоритм ретроанализа. В отличие от алгоритмов шахматной игры он является не приближенным, а точным, что весьма принципиально.

- Но перед его началом надо запомнить все младшие эндшпили, выигранные для белых.

- Позиции с ходом черных, где их король заматован или белые произвели решающее изменение материала (взята черная фигура, белая пешка превращена в фигуру) - перешли в младший выигранный эндшпиль, отнесем к нулевому рангу-РЧ.

- Ну да, белым здесь как бы уже не надо играть (0 ходов).

- Теперь осуществим первый шаг алгоритма. Для этого разобьем все окончания исследуемого класса на два множества "неранжированных" позиций: НБ - с ходом белых и НЧ - с ходом черных (их король не заматован). В НБ выделим все позиции, где у белых имеется хоть один ход, ведущий в РЧ₀. Эти позиции относятся к первому рангу.

- Ясно, белые выигрывают в 1 ход, и, наверное, полученное множество вы обозначите РБ.

- Вы правильно сообразили. Удалим теперь РБ₁ из НБ, а в НЧ выделим все позиции, в которых любой ход ведет в РБ₁ Это также позиции первого ранга, но с ходом черных - РЧ₁, как бы они ни пошли, белые переводят позицию в нулевой ранг, то есть, пользуясь нашей терминологией, выигрывают в 1 ход. Удалим РЧ₁ из НЧ, и этим первый шаг алгоритма исчерпывается. Все готово для начала второго.

- После каждого шага алгоритма, и первого и последующих, в множествах неранжированных позиций НБ и НЧ остается все меньше и меньше элементов. Кажется, я уже и сам могу описать произвольный (n+1)-й шаг алгоритма. Конечно, в предположении, что n шагов уже проделано и к этому моменту получены множества ранжированных позиций: РБ₁, ..., РБ_n, а также РЧ₁, ..., РЧ_n и оставшиеся неранжированными множества НБ и НЧ.

Выделим в НБ позиции, в которых у белых есть хоть один ход, ведущий в РЧ_n. Это позиции ранга (n+1), они образуют множество РБ_n+1, другие позиции пока остаются в НБ. В НЧ выделим позиции, в которых любой ход черных ведет в РБ_n+1 или в позицию с еще меньшим рангом. Это также позиции ранга (n+1), их совокупность РЧ_n+1, оставшиеся позиции - НЧ. Шаг (n+1) завершен.

- Все абсолютно точно!

- Когда же алгоритм заканчивает свою работу?

- Процесс ранжирования завершается, когда очередное множество РБК или РЧК оказывается пустым. Позиции, оставшиеся в НБ и НЧ, не имеют ранга, в них белые не в состоянии выиграть: они либо ничейны, либо даже верх берут черные.

Итак, в процессе работы алгоритма мы не только находим все выигранные для белых позиции, но и устанавливаем, за сколько ходов они достигают цели (ставят мат или проводят решающее упрощение) при наилучшей защите черных. Кстати, весь алгоритм ранжирования легко представить в виде следующей схемы (рис. 41).

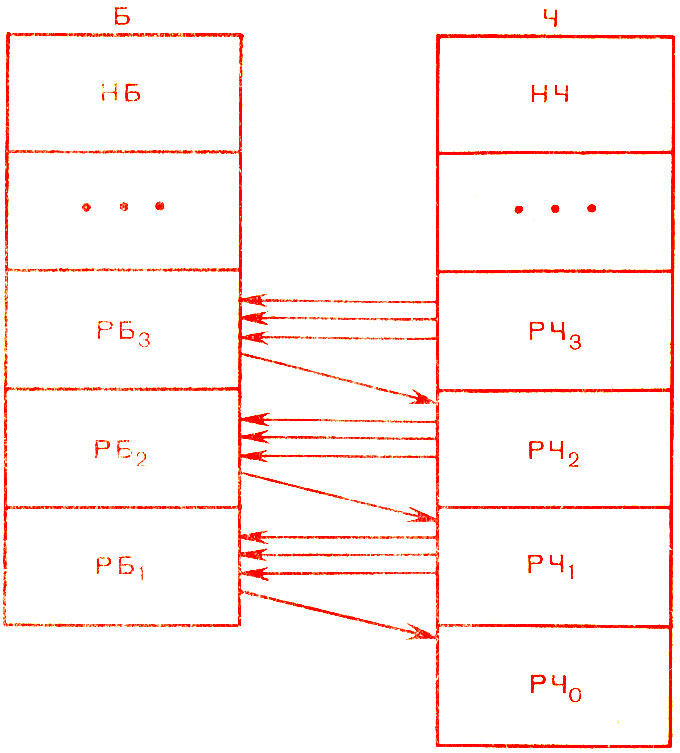
Рис. 41

- Да, она удачно отражает сущность алгоритма. Единственная стрелка, идущая слева направо, отвечает выигрывающему ходу белых, понижающему ранг позиции, а наличие нескольких стрелок, идущих справа налево, отвечает всем ходам черных, ведущим в положение, где белые имеют тот самый выигрывающий ход/

- Описанный алгоритм анализа, как вы смогли убедиться, в самом деле ретроспективный - для оценки позиций мы идем не "вперед", как обычно, а "назад". Полный перебор вариантов при этом не производится, а рассматриваются лишь важнейшие ветви дерева игры: если некоторая позиция охвачена перебором, то алгоритм предлагает белым только такие ходы, которые приближают к цели (понижают ранг позиции на единицу).

- Остался, кстати, еще один невыясненный вопрос. Проведя ретроанализ, машина находит все выигранные для белых позиции и попутно лучшие ходы в каждой из них. А как же быть с позициями, выигранными для черных?

- Вопрос резонный. Все дело в том, что для удобства мы все время рассуждали с точки зрения белых. Практически компьютерная программа проводит ретроанализ одновременно для обеих сторон. В результате каждая позиция получает однозначную оценку - при ходе белых и черных, и если она выиграна, то указывается, какой ход ведет к цели. А поскольку эта позиция появляется в результате процесса ранжирования, то мы одновременно получаем и максимальное число ходов, которое может оказать сопротивление обреченной стороне до перехода в проигранный младший эндшпиль.

- А что можно сказать о ничейных позициях?

- Они, если помните, остаются неранжированными. Это означает, что у данной стороны всегда есть хотя бы один ход, ведущий в другую неранжированную позицию. Таким ходом может оказаться любой, например при двух королях и легкой фигуре на доске. Но часто имеет место и другой вариант: лишь один ход сохраняет "неранжированность". Это не удивительно: и на практике нередко к спасению ведет один-единственный ход.

- Теперь я все понял и могу сказать, что этот интересный алгоритм вполне доступен школьникам, особенно если они увлекаются логическими задачами. Так что вы зря беспокоились и советовали перелистать несколько страниц нашего диалога.

Но возникает вопрос: почему нельзя использовать ретро-анализ для исследования произвольного вида окончаний? Ясно, что вручную можно справиться не с каждой позицией, но на компьютере...

- Вы рассуждаете несколько наивно. Не забывайте, что дело не в исходном положении, а в том множестве позиций, которое оно порождает. Напомню: анализ у нас ретроспективный, и мы отталкиваемся от всех возможных младших эндшпилей. Хотя они образуют лишь малую часть дерева игры, но число их может быть весьма велико. А возникающие при ранжировании два множества - РБК и РЧК могут содержать десятки тысяч позиций. Так что об исследовании вручную не может быть речи даже для самых элементарных случаев. Алгоритм, приспособленный для определенного класса окончаний, необходимо реализовывать на машине. Но и она далеко не всегда сможет провести анализ за разумное время.

- Вы меня убедили. И какие же виды эндшпиля посильны для компьютера?

- На практике для применения ретроанализа необходимо выполнение двух условий, упомянутых выше: во-первых, ЭВМ должна уметь оценивать все младшие эндшпили и, во-вторых, число различных позиций данного вида окончаний не должно быть слишком велико. На сегодняшний день досконально исследованы многие интересные и важные классы окончаний с четырьмя и пятью фигурами (именно их мы обсудим в данном диалоге), а с ростом быстродействия ЭВМ их возможности еще расширятся.

- А для каких окончаний впервые был применен ретро-анализ?

- Для эндшпиля "ферзь с пешкой против ферзя".

- А кто придумал ретро-анализ?

- Этот метод был открыт профессором А. Брудно и, как ни странно, впервые опробован им на машине для одной шахматной головоломки! Но об этом - в нашем заключительном диалоге.

- Хорошо, но мы уже давно собирались перейти к обсуждению серьезных окончаний и позиций.

- Ну что же, пора. Но сначала один забавный случай из шахматной истории.

...В 1968 году в столице состоялся традиционный матч Москва-Ленинград. При счете 39,5:39,5. (игра проходила на 40 досках в два круга) оставалась всего одна незаконченная партия, которая и решала судьбу матча. Ленинградец, игравший черными, имел лишнюю пешку, и в случае успеха его команда побеждала. Доигрывание длилось долго, гости уже опаздывали на поезд, и партия была отдана на присуждение в следующей позиции (рис. 42).

Рис. 42

- Здесь что: выигрыш или ничья?

- Анализом занималась авторитетная гроссмейстерская комиссия, но вся беда в том, что, хотя окончания "ферзь и коневая пешка против ферзя" исследуются уже много лет, до сих пор теория точно не установила, какие из них выиграны, а какие ничейны. Что касается данной позиции, то жюри в растерянности присудило ничью, очевидно, вызвав возражения ленинградцев.

- Если бы компьютер разбирался в таких позициях, недоразумения не произошло бы...

- Поэтому и решено было привлечь компьютер для анализа ферзевых окончаний. Кажется, это был первый эсперимент использования алгоритма ретроанализа для практических целей. И вновь пальма первенства принадлежала "Каиссе"!

- Как "Каиссе", игровой программе? Вы что-то путаете.

- Разумеется, была создана специальная программа для анализа. Но поскольку разрабатывалась она в том же коллективе ученых, что и "Каисса" (основная роль принадлежит математикам Э. Комиссарчику и А. Футеру), то удобно и ее называть по имени богини шахмат. Надеюсь, терминологических недоразумений это не вызовет.

- И каковы успехи машины?

- Программисты решили не браться за все окончания, в которых ферзь с пешкой борются против ферзя, а ограничились позициями с коневой пешкой на предпоследней горизонтали. Но зато, пользуясь ретроанализом, этот класс окончаний "Каисса" изучила досконально и про каждое из них могла точно сказать, выигрывает ли сильнейшая сторона или нет, а если выигрывает, то как быстро.

- В силу симметрии достаточно было изучить позиции с пешкой g7; все результаты автоматически переносятся на позиции с пешкой b7. Кстати, сколько всего положений в данном классе окончаний - при пешке на g7?

- Цифра внушительная - 15 930 523, из них 7 934 157 с ходом белых и 7 996 366 с ходом черных.

- Какие позиции относятся к нулевому рангу? Определив их, мы дальше можем запустить алгоритм ранжирования.

- "Каиссовцы" установили, что этот вид окончаний содержит более пяти миллионов позиций нулевого ранга, которые можно разбить на три основных вида:

1. черный король заматован;
2. белые взяли черного ферзя, а противник не может сделать ничью;
3. белые поставили нового ферзя - g8Ф, и противник тоже не может сделать ничью.

Есть еще ряд младших эндшпилей, которые надо иметь в виду, хотя они могут быть и не выиграны для белых. Например, пешка превращается не в ферзя, а в другую фигуру, или она берет ферзя и одновременно превращается.

- Почему во втором и третьем случаях добавлено условие с ничьей?

- Но ведь взятие ферзя может привести к пату, или черные в ответ берут ферзя, а пешка не проходит. А случается и так, что пешка проходит, а мат ставят черные.

- Обнаружила ли "Каисса" какие-нибудь любопытные позиции?

- Не просто любопытные, она нашла поистине уникальные позиции! Вот пример (ход черных), в котором при наилучшей игре обеих сторон соотношение сил меняется только на 59-м ходу - рекордное число!

Белые: Kpd6, Фa6, и g7; черные: Kpc2, Фb1.

Итак, здесь для выигрыша требуется более 50 ходов!

- Ну да, я совсем забыл, ведь в шахматном кодексе есть пункт, согласно которому партия считается законченной вничью, если обеими сторонами сделано 50 ходов или больше, в течение которых Ни одна из фигур не взята и ни одна из пешек не сдвинулась с места.

Что же получается?! Приведенные позиции выиграны для белых и вместе с тем ничейны! Нелепость какая-то.

- Напомню, что для трех видов окончаний в кодексе сделано исключение и число 50 увеличено до 100.

- Что же это за виды?

- Вот они.

1. Ладья и слон против ладьи.
2. Два коня против пешки, если выполнены условия:
   • а) пешка блокирована конем;
   • б) если пешка черная, то она продвинута не дальше полей a4, b6, c5, b4, e4, f5, g6, h4, а если белая, то не дальше полей a5, b3, c4, d5, e5, f4, g3, h5.
3. Ладья и пешка против слона и пешки, если выполнено одно из условий:
   • а) у белых пешка a2, у черных пешка a3 и чернопольный слон;
   • б) у белых пешка h2, у черных пешка h3 и белопольный слон;
   • в) условия а) и б) с переменой цветов, то есть у черных пешка a7 или h7, а у белых - a6 (и белопольный слон) или h6 (и чернопольный слон).

- Таким образом, "открытие" "Каиссы" показало, что исключения заслуживает и эндшпиль "ферзь и пешка против ферзя".

- В этом и состоит вся уникальность компьютерных находок. Это был первый случай в истории, когда машина вмешалась в шахматный кодекс! Между прочим, в рассматриваемом классе ферзевых окончаний (с пешкой g7) "Каисса" обнаружила 516 (!) позиций, где для победы требуется более 50 ходов (при неподвижной белой пешке).

- В упомянутой вами партии из матча Москва - Ленинград пешка "g" стояла на шестой горизонтали, и, значит, компьютеру осталось сделать всего один шаг, чтобы завершить спор городов...

- В дальнейшем этот эндшпиль был досконально исследован К. Томпсоном, создателем "Белл" - третьей чемпионки мира среди больших ЭВМ. Программа Томпсона проанализировала позиции с белой пешкой на любом поле доски, так что фактически компьютер изучил весь класс окончаний "ферзь и пешка против ферзя". При этом выяснилось, что рекорд продолжительности игры (до решающего размена) принадлежит позиции с пешкой на a6 и равен 71-му ходу! Однако к правилу 50 ходов этот случай отношения не имеет, так как на одном месте (и на a6, и на a7) белая пешка держится меньшее число ходов.

- Наверное, пора перейти к какому-нибудь другому виду окончаний.

- Не спешите. Я еще не рассказал о другом необычном случае, связанном с этим эндшпилем. Именно в нем компьютер впервые оказал практическую помощь гроссмейстеру. Это произошло в 1975 году на зональном турнире в Вильнюсе. Партия Григорян - Бронштейн была отложена в ферзевом окончании с лишней пешкой у черных. Гроссмейстеру было известно об успехах "Каиссы", и он обратился к ней за консультацией. Незадолго до начала доигрывания Бронштейн получил бандероль с подробным анализом позиции. Правда, Григорян уже в начале доигрывания сыграл неточно, и дело обошлось без подсказки "Каиссы"...

- На практике гораздо чаще ферзевых окончаний встречаются ладейные...

- Как раз на них мы и переключим наше внимание. Подробно остановимся на одном из наиболее распространенных и вместе с тем довольно сложных окончаний "ладья и пешка против ладьи". Кстати, сейчас будет уместно вспомнить про международного мастера Д. Леви - страстного любителя пари.

- В предыдущем диалоге речь шла о том, как он вышел победителем в нескольких спорах, скептически оценивая игровые способности машин.

- Но однажды компьютер его сильно подвел...

В середине 70-х годов Леви побывал в Москве- и как-то, беседуя с "каиссовцами", поспорил, что для данного вида эндшпиля невозможно провести исчерпывающий анализ даже с помощью ЭВМ.

- Кто же выиграл пари?

- Компьютер! Затратив 60 часов машинного времени, "Каисса" изучила все ладейные окончания данного вида и теперь в состоянии оценить любое из них.

- Как это было проверено?

- Прошел год после заключения пари, и проверить достижения "Каиссы" пригласили известного специалиста эндшпиля Ю. Авербаха. В Институт проблем управления, где в это время работали создатели "Каиссы", гроссмейстер захватил несколько монографий, посвященных ладейным окончаниям,- компьютеру предстояло серьезное испытание!

Сначала экзаменатор предложил машине ряд простых позиций, и та даже обиделась, она щелкала их как орешки. Наконец, Авербах расставил на доске следующее хитрое положение (рис. 43), полагая, что задал компьютеру каверзную задачку (ход черных).

Рис. 43

Однако после введения позиции в машину та быстро объявила (о положении дел на доске "Каисса" информировала через дисплей), что белые здесь выигрывают, причем после наиболее упорного 1... Лg8 победа достигается через 21 ход. Машина так и сыграла.

- Я бы здесь пошел 2. Лb6.

- Гроссмейстер сразу поставил ладью на h6 и был несколько раздосадован, когда "Каисса" объявила шах - 2... Лg7+, заметив при этом, что белые уже упустили выигрыш.

- Неужели?

- В самом деле, после 3. Кре8 Лg8+ 4. Кре7 Крb7 5. Лh1 Лg7+ 6. Kpf6 Лg4 7. Лс1 Лb4 8. d7 "Каисса" сделала единственный ход 8... ЛЬ6-Н, ведущий к ничьей.

Пришлось Авербаху взять свой ход 2. Лh6 назад. Но после 2. Ле8 Лg7+ 3. Ле7 Лg8 4. Лh7 Kpb7 он снова ошибся - 5. Лb2?, о чем машина не преминула тут же сообщить. Она объявила спасительный шах - 5... Лg7+ у и после 6. Кре6 Лe6+ 7. Кре7 Лg7+ 8. Kpf6 Лg1 играть на выигрыш стало бесполезно.

- Может быть, вместо 5. Лh2 сильнее 5. Kpe6?

- Правильно, в конце концов Авербах так и сыграл, и машина подтвердила, что только этот маневр ведет к цели. После 5... Крс8 6. Кре7 Крb7 7. Kpd7 Kpb8 8. Лh11 атака черных с фланга уже не опасна, и 8... JIg7+ 9. Креб JIg6+ 10. Кре7 Лg7+ 11. Kpf6 Jlg8 12. Kpf7 ЛдЗ 13. Лd1! Лf3 + 14. Кре7 Ле3 + 15. Kpd8 приводит к выигрышу белых.

В заключение "Каиссе" было предложено одно из самых трудных ладейных окончаний (рис. 44). Многие годы им занимались крупнейшие исследователи эндшпиля, пока наконец не была поставлена последняя точка.

Рис. 44

Немного поразмыслив, машина объявила, что здесь выигрывает только 1. Kpc1!

- По-моему, найти такой ход да еще понять, что он единственный, человеку совершенно немыслимо, будь он хоть трижды гроссмейстер.

- Самое интересное, что при наилучших действиях обеих сторон белые здесь продвигают свою пешку лишь на 35-м ходу!

- А если в исходном положении ход черных?

- Тогда они делают ничью: спасает 1... Лh8! и на 2. Kpc1 ладья идет обратно - 2... Лb8!!

- Парадоксально! Мне кажется, что машина, овладевшая столь высокой техникой игры в эндшпиле, может стать прекрасным спарринг-партнером даже для гроссмейстеров. Я уже не говорю о перворазрядниках, таких, как я...

- Быстрые и точные ответы "Каиссы" произвели на Авербаха сильное впечатление, и ему не оставалось ничего другого,

как признать полное превосходство машины над человеком в данном виде ладейных окончаний. Прямо из института он отправился на телеграф и послал в Лондон телеграмму на имя Д. Леви. В ней было всего пять слов: "Поздравляю Новым годом Вы проиграли".

- Не приведете ли один из рекордов для эндшпиля "ладья и пешка против ладьи"?

- Пожалуйста. Взгляните на рисунок 45.

Рис. 45

В этой позиции ход черных - их король под шахом, и соотношение сил меняется только на 60-м ходу, когда белая пешка превращается в ферзя. В главном варианте ходы белых, отмеченные восклицательным знаком,- единственные выигрывающие, а ходы черных с тем же знаком - единственные максимально затягивающие сопротивление.

1. Kpe5!

- Так ли важно, куда ставить короля - на e5 или d5?

- Если бы король сейчас занял соседнее поле, то белые достигали бы цели в два раза быстрее - за 28 ходов!

2. Лc5+! Kpd6! 3. Kpb4! Лb1! 4. Лс2! Лf1 5. Kpb5! Лf5+! 6. Kpb6 Лf8! 7. Лd2+ Кре5! 8. Крс7.

- Некоторые ходы вы не снабжаете восклицательным знаком, то есть они не единственные. Скажем, сейчас можно ли пойти королем на a7 или b7, или вообще дать еще один шах ладьей?

- Ход 8. Kpb7 той же силы, 8. Kpa7 оттягивает достижение цели на два хода, а остальные ходы вообще выпускают победу.

8... Лf4 9. Kpc6 Лc4+! 10. Kpb5! Лc8! 11. Лb2! Лb8+! 12. Kpc6 Kpe6. Как бы вы сейчас сыграли?

- Я считаю, что любой шахматист, не задумываясь, объявил бы здесь шах - 13. Лe2+, отбрасывая черного короля подальше в сторону.

- Полагаю, вы имели в виду шахматиста-человека. Но я вынужден вас удивить, в этом случае после 13... Kpf5! выигрыша уже нет. Но, к счастью для машины, она лишена эмоций и отказывается от первого порыва - дать вертикальный шах...

13. Лb6+!! Смысл горизонтального шаха в том, чтобы передать очередь хода черным. Не достигало цели 13. Лg2 из-за того же ответа 13... Kpf5!

13... Kpe7 14. Лh7+ Kpe6 15. Лb2! Kpe7. Вновь черные могут проиграть вдвое быстрее, продолжая 15... Kpe5 или 15... Kpf5, на что следует 16. Лb5+ и 17. Лb5.

16. Kpc7 Лb4 17. Лe2+. Теперь этот шах решает 17... Kpf7 18. Kpc6 Лb8! 19. Kpc5 Лc8+! 20. Kpd5 Лd8+ 21. Kpc4 Лc8+! 22. Kpd3 Лd8+ 23. Kpc2 Лc8+ 24. Kpb1 Лb8 25. Лe3 Лс18 26. Kpc2.

- Предыдущий ход белых был мне понятен. Из книжки по ладейным окончаниям я помню, что при отрезанном короле черных и "лобовой" атаке их ладьи именно таким способом (Лe3) обеспечивается продвижение пешки вперед. Но сейчас-то она уже могла наконец сдвинуться с места? Сколько же можно, в конце концов, стоять на месте, будто прикованная к цепи?!

- Наберитесь терпения, ждать осталось недолго. Поспешное 26. b3? в один миг губило всю проделанную работу из-за ответа 26... Лс12! Поэтому король снова идет в наступление.

26... Лc8+ 27. Kpd3 Лb8 28. Kpc3 Лс8+ 29. Kpd4 Лd8 + 30. Kpc5 Лc8+ 31. Kpd6 Лb8 32. b3.

- Фантастика! Только на 32-м ходу пешка заявила о себе, да и то как-то робко - двинулась лишь на одно поле вперед!

- Зато теперь дело пойдет быстрее.

32... Лb5 33. Kpc6 Лb8 34. ЛdЗ Kpf8 35. Kpc5 Kpe7 36. b4 Лс8+ 37. Kpb5 Лb8+ 38. Kpa4 Лa8+ 39. Kpb3 Лb8 40. Лd4 Kpe6 41. Kpc4! Kpe5 42. Лd5+ Kpe6 43. b5 Лс8+ 44. Лс5! Лb8 45. Kpb4 Kpe7 46. Kpa5 Kpd6 47. Лg5 Лс8 48. Kpb6 Лd8 49. Kpb7 Лd7 + 50. Kpa6 Лe7 51. b6 Лe3 52. Kpa7 Kpc6 53. Лg3+ Kpb5 54. Лd6 Лf3 55. b7 Лa3 + 56. Kpb8 Лe3 57. Лd2 Kpc6 58. Лa2 Лb3 59. Kpc8 Лe3

- Странный ход. Положение безнадежно, но, взяв на b7, машина могла затянуть сопротивление.

- Вы настолько увлеклись шахматным сюжетом, что совсем забыли о математическом подходе компьютера к своей задаче. Ведь все выигранные для белых младшие эндшпили "Каисса" относит к нулевому рангу. В этом смысле окончания "король и ладья против одинокого короля" и "король, ферзь и ладья против короля и ладьи" для нее равноценны, хотя во втором случае мат дается быстрее.

- По большому счету и для человека безразлично, что получится во время игры: его одинаково устроят оба эндшпиля.

- Вот именно. Итак, хотя после 59... Л:b7 белым нужно всего три хода, чтобы получить решающий материальный перевес: 60. Лс2+ Kpb6 61. Лb2+ и 62. Л:b7, но младший эндшпиль возникает немедленно (после взятия пешки). "Каисса", насколько может, оттягивает переход в такой эндшпиль (60. b8Ф Ле8×).

60. Лс2+ Kpd6 61. b8Ф+, и все кончено.

- Целых 60 ходов на доске не менялось соотношение сил!

- Но к правилу 50 ходов это не имеет отношения, ведь несколько раз двигалась пешка. Хочу заметить, что, приводя те или иные машинные достижения, мы всякий раз приводим лишь одну рекордную позицию, да и то ограничиваемся основным вариантом. Для иллюстрации этого вполне достаточно. В действительности исследования компьютера значительно шире. Он не только находит позиции с максимальной длительностью игры, но и детально разбирает каждую из них: указывает все варианты, ведущие к цели, отмечает, какие ходы являются единственными, какие ведут к удлинению или сокращению решения и какие не влияют на него.

- Сомневаюсь, чтобы человек, каким бы супергроссмейстером он ни был, во время партии, да и в домашнем анализе тоже, сумел бы найти варианты, которые мы только что разобрали.

- Закончим рассмотрение ладейных окончаний настоящей головоломкой (рис. 46).

Рис. 46

Представьте себе, что вы играете белыми, сейчас ход противника, а вам дано право поставить своего короля на любое свободное поле доски. Какое из них вы выберете, чтобы добиться победы?

- Ума не приложу!

- Удивительно, но такое поле всего одно: как установила "Каисса", белые выигрывают только при короле на e8!

- Просто не верится!

- Ну что же, перейдем к другим видам пятифигурных окончаний. Думаю, что интереснее всего эндшпиль "ладья и слон против ладьи". Что вам известно о нем?

- Насколько знаю, он считается теоретически ничейным. Правда, с детства помню позицию Филидора (белые: Kpd6, ЛИ, Cd5; черные Kpd8, Ле7), в которой белые, несколько раз перебрасывая ладью с фланга на фланг, в конце концов берут верх. Но если филидоровскую позицию получить не удается, то на доске ничья.

- Да, но исключений предостаточно, а в турнирах сильнейшая сторона нередко берет верх. Что касается общей оценки эндшпиля, то мы вернемся к этому чуть ниже, а пока очередной рекорд, установленный ЭВМ (рис. 47). В этой позиции белые берут слона и объявляют мат на 59-м ходу.

Рис. 47

- Опять это фатальное число - 59... Ведь и ферзь с пешкой справлялись с ферзем за столько же ходов.

- Совпадение лишь в рангах позиций. Но если в ферзевом окончании за столько ходов мы попадали в выигранный младший эндшпиль, то в данном случае просто ставится мат.

Теперь мне хотелось бы затронуть одну в некотором роде философскую проблему. Вот вы сказали, что окончание "ладья и слон против ладьи" считается теоретически ничейным. А что под этим понимать - "теоретически ничейное", "теоретически выигранное"?

- Можно внести уточнение. Класс выигранных позиций характеризуется тем, что сильнейшая сторона, как правило, берет верх, а класс ничейных - тем, что игра, как правило, заканчивается вничью.

- Верно. Но слова "как правило" напоминают об известном тезисе: нет правил без исключения. А если этих "исключений" окажется слишком много, больше чем самих "правил"?

- Тогда, наверное, придется изменить отношение к данному классу окончаний...

- Как же оценить, сколько "правильных" позиций, а сколько "исключительных"?

- Ну, обычно шахматист-практик это чувствует интуитивно. В принципе следовало бы получить точные статистические данные.

- Вы совершенно правы. Только опираясь на статистику, можно точно охарактеризовать тот или иной вид эндшпиля. Действительно, если доля выигранных позиций близка к 100%, дискуссий о данном классе окончаний не возникает. Ясно, однако, что такой анализ осуществим лишь с помощью ЭВМ.

- Значит, компьютер может поколебать сложившуюся точку зрения?

- Компьютер может все. И вот у меня для вас сюрприз! Программа Томпсона провела статистические подсчеты для окончания "ладья и слон против ладьи" и обнаружила, что доля выигранных позиций составляет 40,1%.

- Удивительное открытие. Даже не знаю, как к нему отнестись. Получается, что нет особых оснований утверждать, что этот эндшпиль ничейный.

- Конечно. Выражаясь математическим языком, можно сказать, что вероятность того, что наугад взятая позиция с ладьей и слоном против ладьи выиграна для сильнейшей стороны, равна 0,4,- весьма высокая. Правда, если говорить о практическом значении этого статистического результата, то надо учесть два сделанных нами допущения:

1. все позиции имеют равные шансы возникнуть в реальной партии;
2. при "доигрывании" и белые, и черные играют наилучшим образом.

- А каковы статистические данные для ферзевых и ладейных окончаний, рассмотренных раньше?

- Они получены для каждого фиксированного положения пешки на вертикалях "a", "b", "c" и "d".

- Ну да, по соображениям симметрии этого достаточно.

- Компьютер установил, что в ферзевом эндшпиле наибольший процент выигранных позиций при белой пешке на d7 (e7) - 85,6%. Если же пешка стоит на a3 (b3), то вероятность победы почти вдвое меньше - 48,5%. В ладейном эндшпиле при белой пешке на d7 (e7) вероятность выигрыша еще выше - 89,1% (абсолютный рекорд), а минимальный шанс при пешке на a2 (h2) - 44%. Те же цифры, очевидно, сохраняются при перемещении пешки на соответствующие поля королевского фланга.

- Как мы убедились, правило 50 ходов не зря было отменено для эндшпиля "ладья и слон против ладьи". А существует ли машинный анализ двух других видов окончаний, отмеченных в кодексе как исключение?

- Два коня, как известно, не матуют одинокого короля. Другое дело, если его сопровождает пешка.

- Алгоритм матования ясен. Один конь блокирует пешку, а другой вместе с королем загоняет неприятельского короля в угол доски, патуя его. Теперь конь-блокер освобождает дорогу пешке и, пока та идет в ферзи, замыкает матовое кольцо.

- Советский этюдист А. Троицкий еще в 30-е годы (очевидно, без помощи ЭВМ) доказал, что в этом эндшпиле для выигрыша, если он есть, нередко требуется более 50 ходов. На рисунке 48 рекордная позиция, найденная недавно компьютером.

Рис. 48

Черного короля удается загнать в правый верхний угол (поле h7), а белый король занимает в этот момент поле f7, свободный конь - поле e6. И лишь на 70-м ходу второй конь покидает свою стоянку, позволяя пешке сделать шаг вперед.

- Нетрудно догадаться, каков финал игры: 71. Kg5+ Kph8 72. Ke5 h1 Ф. Без пешки на доске сейчас стоял бы пат. 73. Kg6×.

- На рисунке 49 рекорд иного рода.

Рис. 49

Белые матуют на 115-м ходу (!), правда, без нарушения правила 50 ходов. Пешка делает шаг вперед на 16, 24, 69 и 113-м ходах, на 114-м превращается в ферзя, и черный король получает мат.

- Но вы не упомянули еще один вид эндшпиля. А его я, кажется, вообще не встречал в теории.

- Действительно, это окончание было исследовано сравнительно недавно, причем занимались им и многие известные гроссмейстеры, в том числе голландец Я. Тимман. Именно он в 1983 году предложил следующую позицию (рис. 50).

Рис. 50

- Наверное, цель белых - перегнать неприятельского короля на правую половину доски, после чего либо он попадает в положение цугцванга, теряя пешку, либо белые отдают качество, обеспечивая беспрепятственное движение вперед своей пешки "a".

- Так и есть, причем в данной рекордной позиции пешка a3 берется лишь на 77-м ходу!

- Результаты анализа эндшпиля "ладья и слон против ладьи" произвели на меня сильное впечатление. А как обстоят дела в эндшпиле, родственном ему,- "ладья и конь против ладьи".

- До вмешательства ЭВМ он был мало исследован и считался "битой ничьей". Но, как выяснилось, и здесь категорические выводы делать рискованно: процент выигранных ситуаций достаточно высок - 35,9%. В рекордной позиции на рисунке 51 белые матуют в, 33 хода.

Рис. 51

- Я слышал, что среди этюдистов в свое время много споров вызывало окончание "два разноцветных слона против коня".

- Некоторые полагали, что оно ничейно, и из этого исходили при составлении этюдов. Однако компьютер разбил эту уверенность в пух и прах, доказав, что сильнейшая сторона почти всегда побеждает - 91,8% выигранных положений. В рекордной позиции коня удается взять лишь на 67-м ходу (рис. 52).

Рис. 52

- Еще один серьезный удар по правилу 50 ходов!

- Решение я, как обычно, опущу - не стану вас утомлять.

- Мы столь подробно обсуждаем успехи машины в анализе эндшпиля, что полезно было бы собрать наиболее яркие компьютерные рекорды вместе. Работа пригодится для шахматной главы будущего издания книги Гиннесса...

- Около десятка шахматных монстров нас еще ждет впереди. Любопытно, что раньше в шахматном кодексе, в правиле 50 ходов, оговаривалось, что если в некоторой позиции для победы необходимо больше 50 ходов (и это можно доказать), то верхний предел следует увеличить до 75 или 100 ходов. Поскольку данным пунктом кодекса никто никогда невоспользовался, в дальнейшем его отменили. Правда, как мы знаем, были сделаны исключения для трех видов окончаний.

- Но теперь, когда компьютеры добились столь внушительных успехов в исследовании эндшпиля, следует признать, что это полумера, и вернуться к старому положению.

- Согласен с вами. Шахматный кодекс должен содержать список всех "исключительных" окончаний и предусматривать возможность его пополнения.

До сих пор мы рассматривали эндшпиль с объективно сложным соотношением сил. На рисунке 53 совсем необычный случай.

Рис. 53

- В чем же необычность? Оценка окончания "ферзь и ладья против ферзя" не вызывает сомнений.

- Сейчас я вас потрясу. В этой позиции белые берут верх на 67-м ходу! Здесь, правда, имеется в виду не переход в младший выигранный эндшпиль (размен ферзей происходит на 55-м ходу), а натуральный мат. Рекорд также установлен программой Томпсона.

- Странное дело! Выходит, что я могу иметь лишнюю ладью, а кодекс неумолимо заставит меня смириться с ничьей. По-моему, законодателям шахматных правил есть над чем задуматься.

- Что поделаешь, перед нами еще одно вмешательство компьютера в шахматный кодекс! На рисунке 54 другая, еще более занятная позиция с тем же соотношением сил.

Рис. 54

- Неужели победа белых в этой партии здесь еще затягивается?

- Предыдущая позиция была рекордной. На сей раз белые, несмотря на лишнюю ладью и свой ход.:, вообще не могут выиграть! При отступлении ладьи противник +сооружает патовое гнездо (1. Ле5 или 1. Лb7- 1... Фd8+), у ферзя нет удачных отступлений, королю же не уйти от шахов. Если же ход черных, им не избежать поражения.

- Я бы сказал, что это редчайшая картина взаимного цугцванга при столь внушительном материальном превосходстве одной из сторон.

- Поразительно, но именно машина доказала единственность подобной конструкции для данного эндшпиля (разумеется, симметрия не в счет: аналогичным образом фигуры могут разместиться и в трех других углах доски).

- Какие еще пятифигурные окончания исследовал компьютер?

- Легко подсчитать, что всего существует 125 видов эндшпиля, в которых белые представлены двумя фигурами, а черные - одной (короли не в счет). Наиболее важные из них мы уже рассмотрели. Надо сказать, что большинство сочетаний фигур не представляет интереса: ферзь или ладья и еще какая-нибудь фигура против слона или коня и т. д. В некоторых окончаниях заслуживают внимания лишь отдельные представители - конь или слон с пешкой против коня или слона. Эндшпиль "две пешки против пешки", хотя и содержит немало нюансов, легко анализируется без помощи компьютера.

- Я встречал этюды с таким финалом: белый ферзь и легкая фигура сражаются с черным ферзем.

- В рекордной позиции ферзь со слоном ставят мат на 33-м ходу, а ферзь с конем - на 41-м. Кстати, многие думают, что при таком соотношении сил выигрыш маловероятен, но компьютер опроверг это мнение. В первом классе окончаний 53,4% выигранных позиций, а во втором - 48,4%.

- Наверное, интересны окончания "ферзь против двух легких фигур"?

- В принципе ферзь легко расправляется с парой неприятельских фигур, а машинная статистика выигранных ситуаций такова: ферзь против слона и коня - 93,1%, ферзь против двух коней - 89,7%, ферзь против двух слонов - 92,1%.

- Почему же на 100%? Впрочем, в исходной позиции королю и ферзю белых может быть объявлена вилка...

- Дело не только в этом. Теории известно немало ситуаций, когда пара легких фигур сооружает неприступную крепость вокруг своего короля. Исследуя эти окончания, машина и здесь вела поиски необычных позиций взаимного цугцванга. Оказалось, что в двух случаях из трех такие конфигурации единственные!

Рис. 55

Посмотрите на рисунок 55. При своем ходе белым не одолеть черного короля (на отступление ферзя следует Cc7 + ), а черные, начиная, быстро проигрывают из-за шаха ферзем с c7 или по линии "b".

И в позиции на рисунке 56 белые, начиная, не могут освободить короля (1. Фa3 Cc8!), а если ход черных, то клубок их фигур мгновенно рассыпается.

Рис. 56

- Приведенные позиции поистине уникальны: во-первых, содержат любопытный шахматный сюжет и, во-вторых, обнаружены компьютером. Указанные вами проценты явно против легких фигур, и если ферзь берет над ними верх, то как долго они могут оказать сопротивление?

- Вот три рекордные позиции, в которых ферзь оказывается на высоте, но вынужден потратить максимум времени, чтобы забрать одну из легких фигур.

- Сколько именно ходов?

- В позиции на рисунке 57, поверьте на слово, белые берут коня или слона только на 42-м ходу.

Рис. 57

- Охотно верю.

- А в положении на рисунке 58 коня удается забрать лишь на 63-м ходу. Надеюсь, вы доверяете машине?!

Рис. 58

- Вполне. Решения чересчур длинные, и я думаю, что не стоит их воспроизводить.

- В заключение еще один рекорд-монстр (рис. 59). Белые берут одного из слонов только на 71-м ходу!

Рис. 59

- Итак, два- рекорда из трех пополняют коллекцию исключений из правила 50 ходов. А последний - так вообще всем рекордам рекорд!

- Среди четырехфигурных окончаний самое интересное "ладья против коня".

- Оно считается теоретически ничейным, но вопрос, ловится ли конь, иногда решается совсем не просто.

- Вы совершенно правы. Эндшпиль на редкость хитрый. А в рекордной позиции на рисунке 60 белые забирают коня на 27-м ходу.

1. Kpd2! Ход на соседнее поле с2 уже выпускает выигрыш. 1... Kd4 2. Kpc3. Выпускает победу 2. Kpd3, впрочем, белым предстоит сделать еще немало единственных ходов, чтобы окружить коня. По-моему, найти их и даже просто запомнить совершенно невозможно. А ведь на доске всего четыре фигуры!

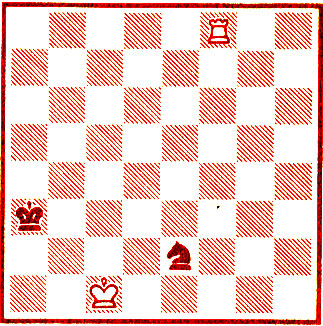
Рис. 60

2... Kb5+ 3. Kpc4 Kd6+ 4. Kpc5 Kb7+ 5. Kpb6 Kd6 6. Лf4! Kpb3 7. Kpc5 Kb7+ 8. Kpc6 Kd8+ 9. Kpb5 Ke6 10. Лf3+ Kpc2 11. Kpc4 Kpd2 12. Лf5 Kpc2 13. Лf2 + Kpd1 14. Kpd3 Kc5+ 15. Kpd4 Kb3+ 16. Kpc3 Kpe1 17. Лb2! Kc5 18. Kpd4 Ke6+ 19. Kpe3 Kpdl 20. Лb6 Kg5 21. Лc6! Kf7 22. Лc7 Ke5 23. Kpe4! Kg4 24. Лg7! Kf6+ 25. Kpe5 Kh5 26. Лg5, и конь пойман.

- Честно говоря, я так и не успел понять, что случилось: фигуры загадочно перемещались по доске, и вдруг конь неожиданно оказался в ловушке.

- Неожиданно только для нас с вами. Машина-то вела свой анализ от конца! Надеюсь, вы не забыли, что эндшпильная программа не столько играет в шахматы, сколько занимается ретроанализом... Если вы не возражаете, давайте сравним два рисунка. На рисунке 61 изображен этюд.

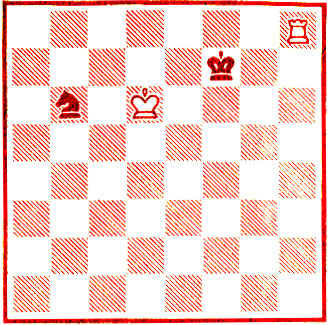
Рис. 61

Справитесь с конем?

- Попробую. 1. Лh4 Kc8 + 2. Kpd7 Kb6+ 3. Kpc6 Kc8 4. Лb7+ Kpf6! 5. Лh6+ Kpg7 6. Лe6 Kpf8! 7. Kpd7 Kpf7 8. Лh6!, и конь в капкане.

- Автор этюда сопровождает основное решение дополнительными вариантами, вот самый длинный из них - 6... Ka7 7. Kpd6! Kpf8 8. Kpd7 Kb5 9. Лc3 Kd4 10. Лe3 Kc2 11. Kpd6 Kpf7 12. Лf3 Kpg6 13. Kpc5 Ke1 14. Лe3 Kc2 15. Лe2 с выигрышем.

Теперь взглянем на другую позицию (рис. 62).

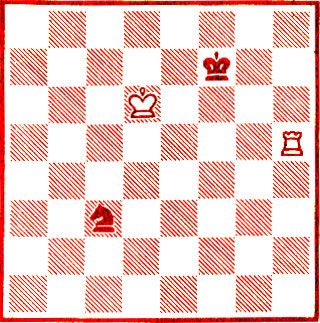
Рис. 62

Программа указала здесь такие ходы: 1. Kpe5 Ka4 2. Лh7 + Kpe8 3. Kpd6 Kb6 4. Лb8+ Kpf7. Дальше можно не продолжать, так как перед нами... исходное положение этюда А. Копнина.

- Вы хотите сказать, что компьютер составил более сложный этюд, чем известный композитор?

- Вот именно!

- Да, есть над чем подумать... А как обстоят дела с эндшпилем "ладья против слона"?

- В нем практически нет положений, вызывающих сомнение в оценке. Интересны, как обычно, позиции с максимальной продолжительностью игры. Рекорд ЭВМ - 18 ходов (рис. 63).

Рис. 63

1. Kpa5! Kpb7 2. Лb3+ Kpa7 3. Лf3! Се2.

- Почему не 3... Cc4?

- После 4. Лc3 Cf1 5. Лc7+ Kpb8 6. Kpb6 получалась выигранная позиция, хорошо известная в теории.

4. Лf7+ Kpb8 5. Kpb6 Kpc8 6. Kpc6. В этом смысл хода Лf3 на третьем ходу, теперь у черных нет спасительного шаха слоном.

6... Kpd8 7. Kpd6 Kpc8 8. Лc7+ Kpb8. Еще одна теоретическая позиция возникает в случае 8... Kpd8, белые выигрывают слона: 9. Лc2 Cd3 10. Лd2! Cg6 11. Лe2 Cf7 12. Лb2 Kpc8 13. Лh8 + Kpb7 14. Лb7.

9. Kpc6 Cc4 10. Kpb6 Cb3. Перед нами выигранная позиция, уже упомянутая выше. 11. Лc3 Ca2 12. Лс2 Cb3 13. Лb2 Ce6 14. Лe2 Cd7 15. Лf2 Ce6 16. Лf8+ Cc8 17. Лb8 Kpa8 18. Л:c8×.

Разобрав этот эндшпиль, обратимся к следующему этюду (рис. 64).

Рис. 64. В. Платов, 1925. Выигрыш

- Все понятно. Решает 1. Кра5 Се2 2. Л!7+ и т.д., а исходная позиция этюда получается из предыдущей только через два хода.

- Причем в положении, предлагаемом ЭВМ, ладья попадает на f3 в процессе решения, что, несомненно, улучшает произведение. Как видите, в активе компьютера, помимо этюда с ладьей против коня, есть и этюд с ладьей против слона.

- Четырехфигурных окончаний в пять раз меньше, чем пяти-фигурных,- 15, я уже подсчитал. Интересно, в каком из них самое длинное решение?

- В эндшпиле "ферзь против ладьи" рекорд составляет 31 ход (рис. 65).

Рис. 65

1. Kpb7 Лb4+ 2. Kpc6 Лc4+ 3. Kpb6 Лb4+ 4. Kpa5 Лc4 5. Фd6 Лd4 6. Фf6 Kpd3 7. Kpb5 Kpe3 8. Kpc5 Лf4 9. Фa1 Лf8. Ладья иногда покидает своего короля, но так, чтобы не попасть под двойной удар. Этот метод защиты, найденный ЭВМ, усложняет задачу белых. 10. Фd4+ Kpe2 11. Фg4 + Kpe3 12. Фe6+ Kpf3 13. Kpd4 Лa8+ 14. Kpe3 Лf8 15. Фe6 + Kpg4 16. Фg6+ Kpf3 17. Фg5. Ферзь, с одной стороны, стремится ограничить подвижность черных фигур, а с другой - прикрывает тыл, обеспечивая приближение собственного короля. 17... Лf4 18. Kpd3 Ла4 19. Фd5+ Kpf2 20. Фс5+ Kpg3 21. Kpe3 Лf4 22. Фh5 Лa4 23. Фe5 + Kph3 24. Фe6+ Kph4 25. Фе7+ Kpg3 26. Фd6 + Kph4 27. Kpf3 Kph5 28. Фd5+ Kph4 29. Фd8+ Kph5 30. Фе8+ Kpg5 31. Ф:а4, и все кончено.

- Для неопытных игроков матование слоном и конем одинокого короля вызывает определенные трудности.

- Машина установила, что для мата требуется не более 33 ходов, это и есть рекорд для четырехфигурных окончаний.

- Матование двумя слонами, наверное, проще.

- Да, здесь достаточно 19 ходов.

- Похоже, наш рассказ о машинных достижениях в анализе эндшпиля подошел к концу...

- Исследование окончаний с пятью фигурами (считая королей), по-видимому, находится на пределе современных возможностей ЭВМ. Однако новые поколения компьютеров, быстродействие которых достигнет многих миллиардов операций в секунду, наверняка смогут анализировать более сложные окончания, с различным числом фигур.

- Восхищаясь искусством анализа окончаний, наверное, стоит упомянуть и об успехах ЭВМ в области композиции. Не правда ли, многие из рекордных позиций, предложенных компьютерами, можно считать этюдами?

- С некоторой натяжкой. Это чисто аналитические позиции, а эстетических, художественных элементов в них маловато.

- А как проявил себя компьютер в составлении задач?

- Шахматные проблемисты часто обращаются к помощи ЭВМ при составлении так называемых кооперативных задач.

- В них цель состоит, кажется, не в том, чтобы заматовать противника, а в том, чтобы получить мат самому.

- Да, при этом начинают черные, которые и помогают противнику пленить их короля. Композитор задается некоторым соотношением сил, затем предлагает компьютеру подобрать позиции на кооперативный мат в заданное число ходов, и остается лишь отобрать лучшие из них.

- Интересно посмотреть один из образцов компьютерного творчества.

- Пожалуйста, на рисунке 66 любопытный пример. Композитора заинтересовала конструкция "белый конь против черного слона".

Рис. 66. Г. Мертес, ЭВМ, 1986. Кооперативный мат в 8 ходов

В каком углу, на ваш взгляд, черный король получит мат?

- Наверное, на поле h8 - оно ближе.

- Тем не менее король идет совсем в другую сторону - 1. Kpd7 Kpf2 2. Kpc6 Kpe3 3. Kpb5 Kpd4 4. Kpa4 Kpc5 5. Kpb3 Kd4+! 6. Kpb2 Kpb4 7. Kpa1 Kpa1 8. Cb1 Kb3×.

- Что можно сказать об ЭВМ не как о составителе, а как о решателе композиций?

- Если в составлении задач и этюдов успехи ЭВМ пока довольно скромные, то в решении - именно задач - с ЭВМ почти невозможно состязаться.

Рис. 67

- Наверное, даже не нужна специальная программа, можно использовать обычную игровую. Вспоминаю, что еще в детстве прочитал где-то о машине, которая за 10 минут расправилась со следующей задачей (рис. 67):

1. e8C! Kp:d6 2. c8Л! и 3. Лc6×; 1... Kp:f6 2. g8Л! и Лg6×.

- Автор этой старинной задачи (1903 г.) - Ф. Хоффман. Но 10 минут для такого простого задания сегодня непозволительная роскошь! Современный компьютер объявит мат за несколько секунд.

- Так или иначе, что стоит машине провести полный перебор вариантов на 2, 3 или 4 хода и заматовать черного короля?

- Ну а если мата нет?! Тогда она все равно предложит какой-нибудь ход. Разбирайся потом, ведет он к цели или нет.

- Да, это не профессиональная работа...

- В этом случае программа должна информировать об отсутствии решения после введения задачи в ЭВМ. Кроме того, машина должна сообщать о побочных решениях и дуалях.

- Уточните, пожалуйста, что это такое.

- Представьте себе, что в задаче-двухходовке, кроме авторского вступления, имеется еще и другое.

- Но такая задача никуда не годится!

- Это и называется побочным решением. Если же первый ход белых единственный, а после ответа черных мат ставится несколькими способами, то мы имеем дело с дуалью. Побочные решения в задаче недопустимы, а дуали в главном, или, как говорят, тематическом (идейном), варианте снижают ее ценность.

- Значит, при решении задач на ЭВМ должен предусматриваться целый ряд проверок: на саму выполнимость задания (и не быстрее, чем положено!), на поиск побочных решений и дуалей.

- Ну и, наконец, компьютер обязан указывать решения задачи при любых защитах черных. Кстати, в современных шахматных программах для персональных ЭВМ, как правило, предусмотрен режим решения задач. Как мы знаем, обязательно имеется он и во всех шахматных микрокомпьютерах.

Между прочим, быстродействующие машины все чаще используются для проверки правильности задач, оказывая неоценимую помощь композиторам. Через компьютеры были "просеяны" многие сборники задач, и под микроскопом ЭВМ нередко обнаруживался серьезный брак: одни задачи содержали побочные решения и дуали, в других мат ставился быстрее, чем положено, третьи вообще не решались. Любопытно, что опровержения задач порой отличаются изяществом и вызывают удивление у самих композиторов.

- Изъяны обнаруживались даже в произведениях знаменитых проблемистов?

Рис. 68. С. Лойд, 1857. Мат в 4 хода

- Они тоже люди... Взгляните на рисунок 68. Содержащееся в книгах решение этой миниатюры довольно симпатичное: 1. Cc3 d5 2. Kpf3 d4 3. Cb3 dc 4. Лd6×.

- И что, мат ставится быстрее?

- Дело не в этом, машина указала довольно грубое побочное решение: 1. Cb6! Kpd2 2. Kpf3 Kp:d1 (2... Kpd3 3. Ce3 и 4. Ce2×) 3. Ce3 и 4. Лc1×; 1. d5 2. Kpf3 d4 3. Ce2+ Kpd2 4. Ca5×.

Посмотрите на рисунок 69.

Рис. 69. Л. Лощинский, Л. Гугель, В. Шиф, 1922. Мат в 2 хода

- Какое же недоразумение могло произойти в двухходовке, неужели композитор просмотрел другой первый ход?

- Опять не угадали. В данной задаче нет побочного решения, потому что нет никакого! Авторский замысел заключался в 1. K:d3 с угрозой 2. Kp:c4×. На 1... Ф:g7 (Ф:f6, C:g7, Лb2, Лa2) с целью перекрыть пятую линию следует 2. K:g7 (соответственно Kd4, Лg7, K:b2, Kb2)×.

- Не помогает и 1... Фa7 (Ф:e6) - 2. Kc7 (Ф:e6)×. По-моему, задача безукоризненна...

- Но вмешивается компьютер и находит блестящее опровержение - 1... Фd7!!, и мата нет, а стало быть, и нет задачи!

- Не слабо. Оказывается, человек, а в данном случае сразу трое композиторов способны пропустить неожиданную реплику даже в двухходовке.

- Для компьютера это просто смешно!

- Да, весьма пикантно, когда машина начисто опровергает задачу. Думаю, что этот пример - редчайший экземпляр.

- Ошибаетесь. Взгляните на задачу, которая несколько лет назад завоевала первый приз на одном из конкурсов (рис. 70).

Рис. 70. В. Сычев, 1983. Мат в 3 хода

Автор указал такое вступление: 1. Фe6!

- Вижу угрозу -2. Лc3+! C(K):c3 3. Cf2×, 2... Kpd4 3. Фd5×.

- Вариантов не так мало, но черный конь и слон то и дело попадают под связку: 1... Cf6 2. Cd2+! Kpf3 3. Лc3×, 1... Cf4 2. Cf2 + ! Kpf3 3. Kd2×, Еще один мат со связкой завершает игру после l...d5 - 2. Ф:e5 Ф:f8 3. Лc3× (2... Ф:e5 3. Kg4×). Наконец, 1... Ф:f8 (Kf5) 2. Cd2+, и мат следующим ходом.

- Ну, что же, довольно яркая задача. Даже не желаю говорить о ее дефектах.

- А зря! Это еще один образец, который вы хотели увидеть. Вновь задача опровергается на первом же ходу!

- Невозможно поверить!

- Опровержение столь парадоксально, что найти его в состоянии только машина! Итак, на 1. Фe6 следует великолепный скачок коня в угол доски - 1... Kh!!, и мата нет и в помине...

Не случайно композиторы любят повторять парадоксальный тезис: нет задач правильных, а есть задачи неопровергнутые!

В принципе компьютер способен помочь композитору не только в проверке задачи на корректность, но и в чисто творческих вопросах. Взяв на себя рутинную работу, ЭВМ позволяет составителю смелее фантазировать, просматривать неизмеримо большее число промежуточных позиций в поисках оптимального расположения фигур.

- Хорошо, с задачами все ясно. Но в решении этюдов, надо полагать, успехи компьютеров скромнее.

- Конечно, ведь число ходов ничем не ограничено. Впрочем, если игра носит комбинационный, форсированный характер, то с этюдом часто справляется обычная игровая программа.

- Возвращаясь к задачам, можно сделать вывод, что при массовом распространении микро-ЭВМ шахматные конкурсы могут потерять свое значение. Не так ли?

- Такая опасность есть. Участник конкурса вполне может доверить позицию машине, а сам отправиться спать... Но ведь мы решаем задачи для своего удовольствия, и нам нет никакого смысла эксплуатировать машину. Что же касается конкурсов, то пусть композиторы придумывают головоломки похитрее, чтобы машине они оказались не по зубам!

Между прочим, конкурсы проводятся не только между решателями, но и между самими композиторами! В таких состязаниях задачи и этюды, представленные авторами, предварительно публикуются в печати, и лишь после их обсуждения и анализа подводятся окончательные итоги. Очевидно, в недалеком будущем компьютерная проверка позволит исключить из рассмотрения все произведения, содержащие изъяны. Объективное судейство будет обеспечено. Вот вам еще один пример компьютерных возможностей!