2. Регулярность; характеризации

2.1. Представимость

Обратимся теперь к рассмотрению некоторых весьма простых и естественных "устройств" для задания языков. Мы увидим, что кажущиеся совершенно различными классы таких устройств эквивалентны в том смысле, что задают один и тот же класс языков. Последнее утверждение составляет содержание теоремы Клини. Эта красивая теорема сейчас, как и раньше, является одним из краеугольных камней теории языков. Она характеризует простейший и широко изучавшийся класс языков, а именно класс регулярных языков. Теорема Клини также хорошо укладывается в нашу общую концепцию морфизмов, поскольку дает характеризацию для языков, получаемых простыми морфическими представлениями.

Понятие представимости мы определим сначала с помощью (конечных) направленных или ориентированных графов (короче, орграфов) G. По определению орграф есть пара G = (V, E), где V - конечное множество, элементы которого называются вершинами, а E - некоторое множество упорядоченных пар элементов из V. Элементы множества E называются стрелками.

В дальнейшем мы будем рассматривать размеченные (labeled) орграфы: каждая стрелка помечается одной или несколькими буквами из алфавита ∑. Кроме того, выделяются два (не обязательно непересекающихся) подмножества V, называемые множествами начальных и заключительных вершин. Размеченный орграф с выделенными начальными и заключительными вершинами называется конечным автоматом. Ниже приводится пример конечного автомата G₁ над алфавитом ∑ = {a, b} с шестью вершинами и шестью стрелками:

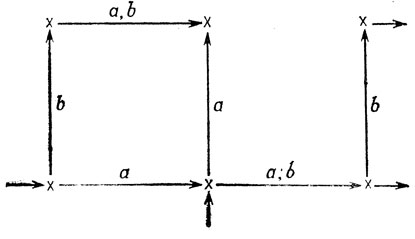
Начальные (соответственно заключительные) вершины отмечены маленькими входящими (соответственно выходящими) стрелками.

Любому конечному пути в размеченном орграфе мы приписываем одно или несколько связанных с ним слов, читая буквы вдоль этого пути. Одному пути может соответствовать несколько слов, если некоторая входящая в этот путь стрелка помечена двумя или более буквами. Обращаясь к нашему примеру, мы видим, что каждое из слов

соответствует некоторому пути из начальной вершины в заключительную, причем слово ab соответствует двум таким путям. (Мы опустили формальное определение пути и соответствующего ему слова, но читатель может при желании определить эти понятия самостоятельно.)

Теперь введем наиболее важное для наших рассмотрений понятие. Язык L(G), представленный конечным автоматом G над алфавитом ∑, состоит из всех слов w над 2, таких, что w соответствует некоторому пути из какой-либо начальной вершины автомата G в какую-либо заключительную его вершину. Считается, что пути, не содержащему стрелок, соответствует пустое слово λ. Следовательно, λ принадлежит языку L(G) тогда и только тогда, когда некоторая начальная вершина одновременно является заключительной.

Таким образом, слова из (2.1) принадлежат языку L(G₁), представленному автоматом G₁ из нашего примера. Легко видеть, что в действительности язык L(G₁) состоит в точности из слов (2.1). Итак, в этом случае язык L(G₁) конечен. Язык L(G₂), который представлен конечным автоматом G₂, определяемым орграфом

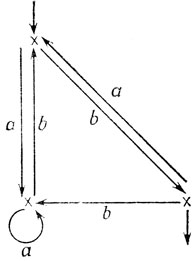
бесконечен, что очевидно, поскольку он содержит, например, все слово вида aⁱb² при i≥1. Читатель может попытаться явно описать весь язык L(G₂). Хотя здесь автомат имеет только три вершины, такое описание не вполне очевидно

Язык L называется представимым, если существует такой конечный автомат G, что L = L(G). Легко видеть (см. упр. 1), что все конечные языки представимы. С другой стороны, например, язык L = {aⁱbⁱ|i≥1} не представим. Интуитивные соображения состоят в том, что конечный автомат способен "считать" только до числа своих вершин и, следовательно, не может порождать язык L. Для более строгого доказательства этого факта надо рассмотреть произвольный конечный автомат G, для которого выполнялось бы условие L(G) = L. Если i превосходит число вершин в G, то любой путь из начальной вершины в заключительную, которому соответствует слово aⁱbⁱ дважды проходит через некоторую вершину на участке, соответствующем подслову aⁱ. Но это означает, что существует число j<i, такое, что слово a^jbⁱ принадлежит L(G), а это противоречит предположению.

Теорема Клини, которая будет доказана ниже, дает исчерпывающую характеризацию представимых языков. Прежде чем перейти к этой теореме, мы обсудим некоторые эквивалентные определения представимости. Их эквивалентность приведенному выше определению будет достаточно очевидна.

Для заданного алфавита ∑ и положительного целого n рассмотрим отображение h алфавита ∑ в множество (n×n)-матриц, элементы которых равны 0 или 1. Отображение h продолжается на ∑* с помощью следующих условий: h (λ) - единичная матрица и для произвольных слов w₁ и w₂ выполняется равенство h(w₁w₂) = h(w₁)h(w₂). (В правой части этого равенства стоит произведение матриц.) Таким образом, h будет морфизмом, отображающим ∑* в мультипликативный моноид (n×n)-матриц.

Рассмотрим теперь n-мерные вектор-строку π и вектор-столбец ζ с элементами 0 и 1 и для заданного слова w∈∑* образуем произведение

Очевидно, для любого w произведение (2.2) является неотрицательным целым числом. Те слова до, для которых произведение (2.2) положительно, образуют язык над ∑, называемый языком, представленным тройкой (h, π, ζ). Говорят, что язык L матрично представим, если для некоторого n он пред" ставим какой-либо тройкой (h, π, ζ).

Лемма 2.1. Язык L представим тогда и только тогда, когда он матрично представим.

Доказательство. Для заданного конечного автомата G над алфавитом 2 построим тройку (h, π, ζ) следующим образом. Пусть n - число вершин в G. Зафиксируем произвольное упорядочение вершин. Для любого i = 1, ..., n 1-й элемент в π (соответственно в ζ) равен 1 тогда и только тогд когда i-я вершина в G является начальной (соответственно заключительной) вершиной. Если i и j - числа, не превосходящие n, а a - элемент ∑, то (i, j)-й элемент матрицы h(a) равен 1 в том и только том случае, когда в G имеется помеченная буквой a стрелка, ведущая из i-й вершины в j-ю.

Наоборот, с данной тройкой (h, π, ζ) подобным же образом можно сопоставить конечный автомат. Таким образом устанавливается взаимно-однозначное соответствие между конечными автоматами G и тройками (h, π, ζ). Мы утверждаем далее, что это соответствие сохраняет представимость языков: если L = L(G) и L₁ представлен тройкой (h, π, ζ), соответствующей G, то L = L₁.

Чтобы доказать это утверждение, покажем по индукции, что при любом k ≥ 0 оба языка L и L₁ содержат одни и те же слова длины k. Это верно для k = 0: оба языка L и L₁ содержат λ в том единственном случае, когда некоторая начальная вершина G является также заключительной вершиной. Пусть по предположению индукции оба языка L и L₁ содержат одни и те же слова длины, меньшей k, и пусть w - слово длины k. Запишем w в виде w = w₁a, где a - некоторая буква. Тогда следующие утверждения эквивалентны:

• (i) w∈L₁;
• (ii) (πh{w₁)) (h(a)ζ) положительно;
• (iii) w₁ принадлежит языку, представленному тройкой (h, π, ζ'), где ζ' получается из h(a)ζ заменой положительных элементов на 1;
• (iv) w₁ принадлежит языку, представленному конечным автоматом G', полученным из G заменой заключительных вершин на те, которые соответствуют вектору ζ';
• (v) w∈L.

В частности, эквивалентность (iii) и (iv) следует из предположения индукции (которое нужно применить к G' тройке (h, π, ζ')). Эквивалентность (i) и (ii), (ii) и (iii) и (iv) и (v) следует из определений и правила умножения матриц. Следовательно, мы завершили индуктивный шаг и тем самым доказали лемму.

Другое, очевидно эквивалентное, определение представимости получается при рассмотрении праволинейных грамматик. Для будущих целей мы введем общее понятие грамматики и различные типы грамматик.

Система подстановок есть пара (∑, P), где ∑ - алфавит, а P - конечное множество упорядоченных пар слов над 2. Элементы (w, u) множества P называются правилами подстановки (или продукциями) и обозначаются w→u. Для данной системы подстановок отношение выводимости ⇒ на множестве ∑* определяется следующим образом. Для любых слов x и y отношение x⇒y имеет место тогда и только тогда, когда существуют такие слова x₁, x₂, w, u, что

и w→u является продукцией системы. Рефлексивное транзитивное замыкание отношения ⇒ обозначается через ⇒*. (Таким образом, x⇒y имеет место тогда и только тогда, когда существуют слова x₁, ..., x_n, такие, что x = x₁, y = x_n и x_⇒1x_i+1 имеет место для каждого i = 1, ..., n-1.)

Грамматикой называется четверка G =(R, ∑_N, ∑_r, ∑_S), где R = (∑, P) - система подстановок, ∑_N и ∑_r - непересекающиеся алфавиты, такие, что ∑ = ∑_N∪∑_r, а ∑_S - подмножество ∑_N. Элементы из ∑_N, ∑_r и ∑_A называются нетерминальными, терминальными и начальными символами соответственно^*. Язык, порождаемый грамматикой G, определяется следующим образом:

^* (Или для кратности нетерминалами, терминалами и аксиомами соответственно.- Прим. перев.)

(Здесь ⇒* есть отношение, определенное системой подстановок R.)

Для i = 0, 1,2, 3 G называется грамматикой типа i, если выполняется i-е из приведенных ниже ограничений, наложенных на систему продукций P.

(0) Никаких ограничений.

(1) Каждая продукция в P имеет вид w₁Aw₂→w₁ww₂, где w₁ и w₂ - произвольные слова над ∑, w - непустое слово над ∑, а A принадлежит ∑_N (с возможным исключением для продукции S→λ, S∈∑_S, вхождение которой в P, однако, влечет невхождение S в правую часть любой продукции).

(2) Каждая продукция имеет вид A→w, где A∈∑_N.

(3) Каждая продукция имеет вид или A→aB, где A, B∈∑_N и a∈∑_r, или A→λ, где A∈∑_N.

Язык, порождаемый грамматикой типа i, называется языком типа i, i = 0, 1,2, 3.

Можно показать, что определенные таким образом четыре семейства языков образуют строго убывающую иерархию, обычно называемую иерархией Хомского. Языки типа 0 называются также рекурсивно перечислимыми. Языки типа 1 (типа 2, типа 3) называются контекстными (соответственно контекстно-свободными, праволинейными). В задачи настоящей книги не входит систематическое исследование этой иерархии, и интересующийся читатель может обратиться к [Sa2].

Для класса языков, рассматриваемых в этой главе, особый- интерес представляют праволинейные грамматики, как показывает следующая лемма.

Лемма 2.2. Язык представим тогда и только тогда, когда он является языком типа 3.

Доказательство. Лемма следует непосредственно из определений. Как и в доказательстве предыдущей леммы, надо построить взаимно-однозначное соответствие между двумя классами представляющих устройств. Кратко поясним, как строится это соответствие.

Для заданного автомата H с множеством вершин ∑_N и алфавитом пометок ∑_r построим праволинейную грамматику G следующим образом. ∑_N и ∑_r суть нетерминальный и терминальный алфавиты соответственно. Алфавит ∑_S состоит из всех начальных вершин. Продукция A→aB принадлежит G тогда и только тогда, когда существует стрелка, помеченная буквой a и ведущая из A в B в автомате H. Далее, продукция A→λ принадлежит G в том и только том случае, когда A является заключительной вершиной в H. Других продукций в G нет. Ясно, что аналогичным образом можно построить автомат H по грамматике G. Это построение сохраняет определяемый язык.▫