По какому месту надо стучать молотком (Глава восьмая) [1973 Шилейко А.В., Шилейко Т.И.

Говорят, что первую половину пути путешественник всегда думает о том, что он оставил, а вторую половину пути - о том, что его ждет впереди. Если применить подобный афоризм к авторам этой книги, то придется сравнить их с путешественниками, совершающими кругосветное путешествие. Чем меньше страниц остается до конца книги, тем острее чувствуется необходимость вернуться к вопросам, поставленным в самом начале.
В предисловии мы определили кибернетику, как науку о том, по какому месту надо стучать молотком

Ответили ли мы на этот вопрос? В предыдущих главах были рассмотрены всевозможные автоматические системы. Попутно нам удалось ответить на целый ряд вопросов, в частности, когда нужно подавать управляющее воздействие и какой вид должно иметь это воздействие. Единственный вопрос, который так ни разу и не возник на предыдущих страницах, это где или, более правильно, к какой именно точке системы управляющее воздействие должно быть приложено. Рассматривая возможные конструкции регулятора паровой машины, мы предполагали, что управлять скоростью этой машины можно и нужно одним-единственным способом - поворачивая заслонку в трубе, подводящей пар в цилиндр. Так ли это на самом деле? И действительно ли вопрос о точке приложения управляющих воздействий всегда .решается так же просто, как в случае паровой машины?

На первый взгляд кажется, что так оно и есть. Чтобы изменить направление движения автомобиля, надо повернуть баранку, а чтобы увеличить его скорость - нажать на акселератор. Чтобы заставить сокращаться мышцу лягушачьей лапки, надо приложить электрическое напряжение к спинному нерву. Наконец, чтобы убить мамонта, надо приложить воздействие к шесту, поддерживающему камень. Правда, того же эффекта можно было бы добиться, постукивая другим камнем по основанию скалы, но вряд ли такой способ мог прийти в голову конструктору ловушки для мамонта и его последователям.

Ясно одно - во всех рассмотренных в этой книге примерах вопрос о точке приложения управляющего воздействия представляется исключительно простым. Но это простота кажущаяся. Объясняется она тем, что, во-первых, мы сознательно рассматривали системы, уже приспособленные для управления, т. е. автомобиль, снабженный сложной системой рычагов, передающих движение от рулевой баранки к передним колесам, паровую машину с заслонкой в паропроводящей трубе и т. п. Во-вторых, и это значительно важнее, мы ни разу не поставили вопроса об эффективности управления.

Вернемся еще раз к паровой машине. Предположим, что нагрузка упала до минимума и чтобы поддерживать нужное значение скорости вращения вала, нам пришлось почти полностью прикрыть заслонку. Рассматривая подобную ситуацию в пятой главе, мы предполагали, что давление пара остается постоянным. Но прикрывая заслонку, мы уменьшаем расход пара. Если топка котла продолжает работать с прежней интенсивностью, то единственная возможность поддерживать давление пара постоянным состоит в том, чтобы выпускать излишек пара через предохранительный клапан котла. Так и делается на самом деле. Но спрашивается, что в этом хорошего? Ведь драгоценное топливо затрачивается теперь в прямом смысле этого слова на ветер.

Как же избежать подобной непроизводительной затраты топлива при уменьшении нагрузки тепловой электростанции? Казалось бы, сделать это достаточно просто, если соединить рычаг центробежного регулятора не с заслонкой в пароподводящей трубе, а с такой же точно заслонкой в трубе, подводящей нефть к топке (или подводящей воздух, если топка угольная). Это действительно можно осуществить. Но ведь паровой котел с топкой - система значительно более инерционная, чем маховик паровой машины. Если ПИД-регулятор должен был предугадывать факт увеличения скорости за несколько секунд или даже за несколько долей секунды до того, как он может наступить на самом деле, то регулятор, поддерживающий скорость постоянной путем изменения количества подаваемого топлива или интенсивности его горения, должен предугадывать возможное изменение скорости уже за несколько минут до того, как оно должно наступить. Ясно, что такой регулятор будет значительно сложнее, а сложнее, значит, дороже.

Есть и еще один способ, сводящийся к тому, чтобы попросту препятствовать изменению нагрузки. Т1менно так и поступают в настоящее время, соединяя отдельные электростанции в так называемое энергетическое кольцо. Энергетическое кольцо охватывает области, расположенные в различных часовых поясах. Если, например, в том месте, где расположена данная электростанция, наступила ночь и энергии потребляется мало, электростанция переключается на питание других областей, где еще только наступает вечер. Наоборот, в часы, когда в данной области потребление максимально, другие электростанции кольца передают ей часть своей энергии.

Чтобы такое кольцо работало правильно, снова нужно управление. Но здесь точками приложения управляющих воздействий оказываются уже распределительные устройства, включаемые не на.входе, а на выходе паровой машины, а точнее, на выходе генератора, приводимого в движение паровой машиной.

Даже из этого простого примера видно, что вопрос о точках приложения управляющих воздействий совсем не так прост, как нам казалось на первый взгляд. Более того, мы получили некоторое представление о том, как надо искать подобные точки. Можно сказать, что среди нескольких возможных управляющих систем наиболее эффективной оказывается та, которая осуществляет качественное управление при минимальных затратах. Что такое затраты, понять легко, но вот, что такое "качественное управление"? Этот вопрос подводит нас к другому, значительно более общему вопросу: а почему вообще нужно управлять?

В первой главе этой книги мы упомянули вскользь один из всеобщих законов природы, называемый вторым началом термодинамики. Простейшая формулировка этого закона, ставшая в последнее время классической, во всяком случае для популярной литературы, гласит: природа стремится к беспорядку. Но откуда у природы столь странные стремления и что такое беспорядок вообще, чем от отличается от порядка?

Ответы на эти вопросы требуют некоторой подготовки, поэтому давайте перенесемся на некоторое время в область фантастики. Рассмотрим ситуацию, столь полюбившуюся авторам научно-фантастических произведений. Звездолет садится на неизвестную планету. Открываются люки, астронавты спускаются на обожженный выхлопом грунт и вдруг обнаруживают совершенно правильный белый квадрат на сером фоне скалы. Ни у кого не остается ни малейших сомнений в том, что планета населена разумными существами. Правильный квадрат есть несомненный признак разумной деятельности. Но почему? Почему тончайшая игра красок на закатном небе, которую, к слову сказать, еще не удалось в точности воспроизвести ни одному, даже самому гениальному художнику, - это игра неразумной природы, ко всему прочему стремящейся к беспорядку, а вот квадрат - это обязательно признак присутствия разума? Снова вопрос, и снова ответ на него требует некоторой подготовки.

Пусть имеется мешок с несколькими сотнями карточек или фишек, причем на каждой карточке изображена одна из букв русского алфавита. Вытащим из мешка наугад четыре карточки и разложим их на столе слева направо в том порядке, в каком мы вынимали их из мешка: Какова вероятность того, что при этом получится осмысленное русское слово? В словаре русского языка содержится всего около тысячи четырехбуквенных слов, включая такие архаичные слова, как "веды", и такие заимствованные из других языков слова, как, например, "герц". Общее количество возможных сочетаний из 32 букв по 4 равно, очевидно, 324 = 1048 576. Следовательно, вероятность вытащить из мешка четыре карточки с такими буквами и в таком порядке, чтобы из них составилось осмысленное русское слово, немногим меньше одной тысячной. Еще меньше вероятность составить, вытаскивая карточки из мешка наугад, какое-нибудь данное слово, например слово "стол". Эта вероятность, согласно сказанному выше, меньше одной миллионной. И, наконец, совсем уж исчезающе мала вероятность составить два одинаковых слова подряд. С позиций математики такая вероятность меньше чем Ю-12, а с позиций "здравого смысла" мы вправе утверждать, что такого не бывает.

Предположим теперь, что мы написали те же буквы на гальке морского берега. На каждом камешке по одной букве. Волны прибоя все время перемешивают камешки. При этом каждый раз возникает какое-то сочетание букв, в том числе могут, конечно, получаться и осмысленные сочетания. Однако поскольку осмысленных сочетаний значительно меньше, чем неосмысленных, то вероятность появления осмысленного сочетания значительно меньше, а следовательно, как мы показали это в главе шестой, появляться они будут исключительно редко. По этой же причине, если мы сами выложим из камешков с буквами какое-нибудь слово, то совершенно естественно, что первый же удар волны разрушит это слово и заменит его бессмысленным, на наш взгляд, сочетанием букв.

Теперь мы можем уже сделать некоторые выводы. Все окружающие нас предметы, которые мы объединяем под одним понятием "природа", состоят из бесчисленного множества частей, а эти части в свою очередь состоят из бесчисленного множества частиц. Все эти части и частицы находятся в непрерывном движении - таково основное и главнейшее свойство природы, т. е. материального мира. Двигаясь, они естественным образом предстают перед нами каждый раз в различных сочетаниях. Каждое отдельное сочетание по-своему неповторимо, поскольку вероятность его реализации исчезающе мала.

Мы сами как бы делим эти сочетания на два различных класса: сочетания, принадлежащие к одному из классов, мы называем порядком, а сочетания, принадлежащие к другому классу, - беспорядком. Именно потому что к классу "порядок" относится значительно меньше сочетаний, чем к классу "беспорядок", вероятность порядка значительно меньше. Так, в нашем примере с четырехбуквенными словами к классу "порядок" относилось всего лишь 1 000 возможных сочетаний, в то время как к классу "беспорядок" - остальные 1 047 576 сочетаний. Следовательно, слова "природа стремится к беспорядку" надо понимать так: природа не предпочитает одних сочетаний другим. Если мы и вправе в чем-то обвинять природу, то только в безразличии, но отнюдь не в коварных намерениях. Скорее наоборот, именно безразличие природы, приводящее к тому, что каждый раз возникает одно какое-либо сочетание составляющих ее частей и частиц, причем это сочетание немедленно сменяется другим сочетанием, не схожим с предыдущим, и послужило причиной тому, что в числе прочих возникают и те сочетания, которые мы склонны теперь относить к классу порядка. Прекрасно сказано об этом в поэме "О природе вещей", написанной древнеримским поэтом и философом Титом Лукрецием Каром в I веке до нашей эры:

^* (Лукреций, О природе вещей. Пер. с латинского Ф. А. Петровского. Изд. АН СССР, 1946, книга пятая, стр. 293, строки 963-966. )

Сформулируем теперь некоторые определения, что значительно упростит нам дальнейшее изложение. Так, всякую совокупность конечного числа материальных объектов мы будем называть физической системой или просто системой, а составляющие ее материальные объекты - элементами этой системы. Заметим, и это очень важно, что рассматривая некий объект - как элемент системы, мы предполагаем, что сам он не изменяется хотя бы в течение того времени, пока мы наблюдаем систему, и не может быть разделен на более мелкие элементы. Так, например, рассматривая мешок с карточками, на которых написаны буквы, мы считаем, что в течение всего времени, пока мы производим эксперименты с этим мешком, т. е. вытаскиваем из него карточки, ни одна из карточек не окажется разорванной пополам (что в принципе, конечно, возможно) и, например, буква А не превратится в букву Л из-за того, что в результате частого хватания руками у буквы А сотрется перекладина.

Элементы системы находятся в непрерывном движении и вследствие этого каждый раз выступают перед нами в различных сочетаниях. Отдельное сочетание, которое можно отличить от других сочетаний, мы будем называть состоянием системы, независимо от того, имеет ли это состояние какой-нибудь смысл. При таких условиях выдвинутый выше тезис о безразличии природы можно сформулировать еще и следующим образом: все состояния физической системы равновероятны.

Некоторую определенную совокупность различных состояний мы будем называть конфигурацией. Так, например, всякое состояние физической системы "мешок с карточками", при котором вынутые из мешка карточки (точнее, буквы, написанные на этих карточках) составляют слово, имеющее смысл в русском языке, мы будем относить к конфигурации "слово". Все остальные возможные состояния относятся к конфигурации "не слово".

Конечно, конфигураций может быть больше, чем две. Так, например, конфигурацию "слово" можно подразделить на ряд более мелких конфигураций: существительное, глагол и т. д.

Назовем физическую систему организованной, если она в течение достаточно длительного времени остается в пределах некоторой данной конфигурации. Это ни в коей мере не означает прекращения изменения ее состояния. Движение продолжается, и состояния непрерывно сменяются одно другим. Однако в организованной системе это движение происходит таким образом, что каждое новое состояние оказывается относящимся к той же самой конфигурации, что и предыдущее.

Теперь все зависит от того, как определить конфигурацию. Если считать, например, что все возможные состояния данной физической системы относятся к одной и той же конфигурации или, возвращаясь к мешку с карточками, считать, что любое сочетание из четырех букв - это слово, то ясно, что система всегда будет находиться в пределах этой конфигурации. Можно поступить иначе, условившись, например, считать словом любые сочетания из четырех букв, начинающиеся с букв А, Б и т. д. до П, и не словом - любые сочетания из четырех букв, начинающиеся с букв Р, С и т. д. до Я. Ясно, что при таком условии система, в которой все состояния равновероятны, будет относиться к конфигурации "слово" лишь в половине общего числа возможных случаев. А для того чтобы постоянно удерживать ее в пределах конфигурации "слово", необходимо произвести какие-то дополнительные действия. Например, все карточки с буквами от А до П сделать из железа, карточки с буквами от Р до Я сделать из меди и вытаскивать первую карточку с помощью магнита, а остальные три - просто руками.

Последнее замечание содержит явный намек на то, каким образом можно изменять вероятности состояний. Однако мы не будем пока вдаваться в обсуждение этой возможности, а сделаем другое, более общее наблюдение. Действительно, сказанное выше наводит на мысль о том, что, определяя конфигурацию, мы тем самым определяем и степень организованности системы. Ведь само слово "организованность" предполагает выполнение каких-то действий по организации. С другой стороны, если конфигурация такова, что к ней могут относиться все без исключения возможные состояния системы, то вряд ли есть основания считать систему, находящуюся в пределах этой конфигурации, организованной.

Все сказанное непосредственно приводит нас к следующему выводу: степень организованности системы, находящейся в течение длительного времени в пределах данной конфигурации, тем выше, чем меньше вероятность самопроизвольного нахождения системы в пределах этой конфигурации,

Иными словами, каждой конфигурации системы можно поставить в соответствие определенную величину, которая будет характеризовать степень организованности системы, если она остается в пределах данной конфигурации.

Согласно сказанному выше в качестве такой величины, казалось бы, естественно выбрать величину, обратную вероятности самопроизвольного нахождения системы в пределах данной конфигурации. Но здесь появляется одна трудность.

Мы уже предложили один из способов организации системы "мешок с карточками", состоявший в том, чтобы изготовлять карточки из двух различных материалов - меди и железа, а для вытаскивания пользоваться магнитом Теперь мы несколько видоизменим этот способ. Пусть по-прежнему буквы от А до П написаны на железных карточках, а буквы от Р до Я - на медных. Однако мы не будем использовать магнит, а перед тем, как вытаскивать первую карточку из мешка, мы взвесим ее и вытащим, если она легкая (железная), и не вытащим, если она тяжелая (медная). Поскольку железных и медных карточек в мешке поровну, чтобы выбрать нужную карточку, мы в среднем затратим два взвешивания.

Итак, чтобы вытащить из мешка одну четверку карточек, относящихся к конфигурации "слово", необходимо выполнить два взвешивания (в среднем); чтобы вытащить подряд две четверки карточек, относящихся к конфигурации "слово", нужно выполнить четыре взвешивания, и т. д. по два взвешивания на каждую следующую четверку. Другими словами, количество усилий, затрачиваемых на организацию системы, оказывается равным количеству усилий, затрачиваемых на одну попытку такой организации, умноженному на количество попыток. Это также совершенно естественно.

Иначе будет обстоять дело, если за меру организованности мы примем, как это предлагалось выше, величину, обратную вероятности самопроизвольного прихода системы в пределы данной конфигурации. Так, если по-прежнему вытаскивать карточки наугад, невзирая на их вес, то вероятность вытащить четверку карточек, относящуюся к конфигурации "слово", будет равна ½, вероятность вытащить две такие четверки подряд будет равна ¼, вероятность вытащить три такие четверки будет равна 1/8 и т. д. Величины, обратные вероятностям, умножаются, а не складываются, что явно противоречит нашему естественному представлению о том, какой должна быть мера степени организованности.

Поэтому в качестве меры степени организованности системы берут не величину, обратную вероятности, а логарифм этой величины - ведь логарифм произведения равен сумме логарифмов сомножителей. Но мы уже знаем, что если все состояния системы равновероятны, то вероятность для системы оказаться в пределах данной конфигурации пропорциональна количеству состояний, составляющих эту конфигурацию, или, иными словами, пропорциональна количеству способов, которыми может быть построена данная конфигурация

Установим теперь окончательно, что за меру организованности физической системы, находящейся в течение достаточно длительного времени в пределах данной конфигурации, мы принимаем логарифм величины обратной вероятности того, что система самопроизвольно окажется в пределах данной конфигурации, или взятый со.знаком минус логарифм этой вероятности, или же, наконец, величину, пропорциональную взятому со знаком минус логарифму от числа способов, которыми может быть реализована данная конфигурация. В математической записи это выглядит так:

где p - вероятность для системы находиться в пределах данной конфигурации; γ - количество способов, которыми может быть реализована данная конфигурация; k - постоянный коэффициент.

Та же самая величина, но взятая с противоположным знаком, получила в физике название энтропии. Используя те же обозначения для энтропии, мы можем записать:

Ясно, что величина энтропии тем больше, чем больше вероятность конфигурации, в которой находится система. Выражение энтропия всякой физической системы стремится к возрастанию - представляет собой еще одну, правда, не очень четкую, формулировку второго начала термодинамики.

На самом деле, мы установили выше, что энтропия, равно как и сама физическая система, ни к чему не стремится, во всяком случае в указанном выше смысле. Просто если органичиваться рассмотрением таких систем, как, например, галька на морском берегу, то здесь отсутствуют какие-либо условия, делающие одно конкретное сочетание камешков предпочтительнее другого. Поэтому чем больше различных сочетаний составляют конфигурацию, тем больше вероятность этой конфигурации и тем чаще она наблюдается на самом деле. С другой стороны, если случайно или под воздействием каких-либо внешних причин установилось одно какое-либо сочетание и мы выделяем это сочетание как самостоятельную конфигурацию, то чрезвычайно велика вероятность того, что в ближайший момент времени это сочетание будет нарушено и система перейдет к другой конфигурации, более вероятной.

Все сказанное до сих пор на страницах этой книги позволяет нам утверждать, что цель управления состоит в поддержании физической системы в пределах конфигурации, обладающей малой вероятностью самопроизвольного возникновения. Иными словами, цель управления - понизить энтропию системы или повысить степень ее организации. Все три только что высказанные формулировки полностью эквивалентны друг другу.

Рассмотрим снова самую простую систему - паровую машину. Будем считать, что состояние паровой машины определяется всего лишь тремя факторами: давлением пара, положением заслонки и величиной нагрузки. Если полностью отсутствуют какие-либо регулирующие воздействия, у нас нет никаких оснований предпочесть одну величину угла поворота заслонки всем остальным. То же самое можно сказать и по отношению давления пара или величины нагрузки. Следовательно, мы имеем множество возможных сочетаний значений этих трех параметров и все они равновероятны.

Введем в рассмотрение две различные конфигурации, одна из которых имеет место тогда, когда скорость вращения вала находится в данных пределах, а другая - когда скорость вращения вала имеет произвольное значение. Первая конфигурация может иметь место при достаточно большом количестве различных сочетаний значений параметров. Например, когда давление пара минимально, а заслонка открыта полностью; когда давление пара максимально, нагрузка минимальна, а заслонка только чуть приоткрыта и т. п. В то же время очевидно, что количество сочетаний значений параметров, обеспечивающих произвольное значение скорости, значительно больше. Поэтому есть все основания ожидать, что паровая машина без регулятора будет находиться в пределах второй конфигурации, имеющей большую вероятность. Однако стоит нам соединить заслонку с рычагом регулятора Уатта, как положение резко меняется. Более вероятной становится первая конфигурация, и большую часть времени система находится в пределах этой конфигурации.

Но соединяя заслонку с рычагом регулятора Уатта, мы, вообще говоря, не изменяем вероятностей отдельных ее положений. Наоборот, если по-прежнему считать, что давление пара и нагрузка изменяются произвольно, то и положение заслонки также будет изменяться произвольно и у нас нет никаких оснований предпочесть одно какое-либо положение заслонки всем остальным. Следовательно, все три введенные нами в рассмотрение параметра, взятые по отдельности, по-прежнему могут изменяться так, что все возможные их значения равновероятны. А вот количество сочетаний значений этих параметров уменьшилось, потому что, введя управление, мы поставили значения одного из параметров в зависимость от значений двух других. Иначе, мы сделали движения заслонки согласованными с движениями других частей системы. Безразличию природы мы противопоставили согласованность, или целенаправленность действий в искусственно созданном механизме.

Рассмотрим теперь еще более простой случай. Пусть давление пара остается постоянным, а изменяется только нагрузка. Предположим также, что нагрузка изменяется случайным образом, и, следовательно, мы ничего не можем сказать о возможных значениях величины этой нагрузки кроме того, что каждое такое значение имеет определенную вероятность.

Обозначим через р{х) вероятность того, что в ближайший момент времени значение величины нагрузки будет заключено между х и х+Δх, где Δx - наперед заданная малая величина. Напомним читателю, что величину р(х) можно вычислить, если в течение очень долгого времени производить замеры величины нагрузки, например каждую секунду, и затем поделить количество случаев, когда значение измеренной величины оказывалось заключенным между х и Δх, на общее количество замеров. Чем больше количество замеров, тем ближе результат деления к истинному значению вероятности. Выбирая для величины х различные значения в пределах возможного диапазона изменения нагрузки, мы можем аналогичным образом вычислить вероятность для всех этих значений.

Заметим теперь, что для каждого конкретного значения величины нагрузки (при условии, что давление пара постоянно) существует такое положение заслонки, при котором скорость вращения вала находится в заданных пределах. Предположим снова, что управление полностью отсутствует и положение заслонки совершенно произвольно. Тогда мы опять-таки можем говорить только о вероятности р(у) того, что значение угла поворота заслонки а заключено в пределах между у и Δу, где Δy - некоторая малая величина.

Примем полную величину диапазона возможных изменений нагрузки за единицу, а величину Ах выберем равной, например, 0,001. Если к тому же предположить, что все значения величины нагрузки равновероятны, то величина вероятности р(х) для любого х, очевидно, окажется равной 0,001.

Проделаем то же самое с заслонкой, т. е. примем величину полного возможного угла поворота заслонки за единицу, а Δу положим равным 0,001. Если считать все положения заслонки равновероятными, то р(у) также окажется равным 0,001 для любого у.

Итак, факт, состоящий в том, что величина нагрузки имеет данное значение, и факт, состоящий в том, что угол поворота заслонки имеет данное значение, - это случайные события, которые можно характеризовать только вероятностью их наступления.

Рассмотрим теперь события, состоящие в том, что нагрузка имеет величину х, а угол поворота заслонки имеет величину у, причем у таково, что скорость вращения вала машины находится в заданных пределах. Вероятность подобного события обозначим через р(х, у). Какова же будет эта вероятность? Из сказанного ясно, что р{х,у) - это вероятность одновременного наступления двух событий, причем в случае полного отсутствия управления это вероятность одновременного наступления двух независимых событий. А коли так, мы вправе применить рассмотренную в главе теорему умножения вероятностей и положить

Так оно и есть на самом деле! Если все сделанные выше предположения справедливы, то ситуация, когда заслонка паровой машины случайно установится именно в то положение, которое необходимо для поддержания данной скорости, может встретиться в среднем лишь один раз на миллион случаев.

С другой стороны, вводя управление, мы повышаем вероятность р(х, у). Заметим, что мы повышаем именно вероятность, поскольку, как это следует из сказанного в главе пятой, даже самая совершенная система управления не может гарантировать нам, что заслонка окажется в нужном положении во всех без исключения случаях. Еще более справедливым это утверждение оказывается для более сложных систем, рассмотренных в главе шестой. Следовательно, мерой согласованности между движением заслонки и изменением нагрузки мы с полным основанием можем считать величину, показывающую, насколько р(х,у) при наличии управления превышает значение р(х)р(у), т. е. величину той же вероятности при отсутствии управления.

С учетом соображений, которые были развиты нами выше при выводе меры организованности системы, примем теперь величину

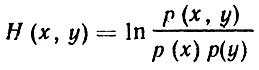
за меру качества управления. Величина Н(х, у) называется взаимной информацией случайных событий х и у или, иначе, количеством информации, содержащейся в событии у относительно события х. Так мы пришли к еще одному важнейшему понятию, рассматриваемому в рамках кибернетики, - понятию информации. Мы установили также, что чем больше информации о поведении внешней среды несет с собой управляющее воздействие, тем выше качество управления.

И все же мы должны констатировать, что, даже достигнув высокого качества управления, конструктор управляющей системы еще не может считать себя полностью удовлетворенным. И правда, стоит ли городить сложные и дорогие управляющие системы для той же паровой машины, если, как это было рассмотрено в начале главы, большая часть пара из котла через предохранительный клапан будет уходить на ветер? Ясно, что, кроме качества управления, важны еще общие затраты на работу системы в целом. Последнее соображение позволяет нам определить эффективность системы автоматического управления как отношение качества управления к общим затратам.

Так по какому же месту надо стучать молотком? Сумеем ли мы теперь, пройдя столь долгий путь и познакомившись с принципом действия новейшего чуда современности - цифровых вычислительных машин, получить удовлетворительный ответ на этот вопрос. К сожалению, нет. Тайна Николая Ивановича по-прежнему остается нераскрытой.

Но многое мы все же знаем. Во-первых, мы знаем, что мест, по которым можно стучать молотком, много. Точнее, каждая система имеет несколько точек, к которым можно прикладывать управляющее воздействие, причем чем сложнее система, тем таких точек больше. Во-вторых, мы знаем, что, выбирая одну какую-либо точку для приложения управляющего воздействия, мы должны выбрать также соответствующую стратегию управления. Стратегий таких много, но лучше из них та, при которой качество управления оказывается более высоким. Наконец, мы знаем, к чему стремиться, проектируя автоматическую систему управления. Стремиться надо к тому, чтобы наиболее высокой оказалась эффективность управления.

Как же надо строить эффективную систему управления? Современная теория автоматического управления располагает многими средствами решения этой задачи. Все эти средства, однако, можно свести к двум основным группам. Первая из них - это составление математических моделей. Суть всех методов, относящихся к этой группе, состоит в том, что знание, имеющееся у нас об объекте управления, мы используем для того, чтобы составить математическое описание. Располагая таким описанием, достаточно просто определить, изменение каких именно параметров в наибольшей мере влияет на конечный результат, а следовательно, узнать и точки возможных приложений управляющих воздействий. Используемые при этом методы объединяются сейчас под общим названием теория чувствительности. Затем составляется такое же точно математическое описание системы управления и проверяется, как объект и система управления работают совместно. Отдельные параметры системы управления изменяются до тех пор, пока не будет достигнуто наибольшее возможное значение эффективности. Все это можно проделать с помощью цифровой вычислительной машины, и тогда мы приходим к тому, что принято называть сейчас автоматическим проектированием

Вторая группа методов основывается на общей идее обучения. Система управления, которая обязательно содержит в этом случае цифровую вычислительную машину, подсоединяется к объекту. Первоначально системе не задается никакой стратегии управления. Устанавливается только цель, которая, как было установлено выше, состоит в достижении наибольшей эффективности. Стратегия управления вырабатывается постепенно методом проб и ошибок точно так же, как это было описано в предыдущей главе. Таким образом создаются адаптивные (приспосабливающиеся) самообучающиеся системы

Рассмотрим в заключение этой главы еще один вопрос. Выше мы безоговорочно приняли тезис о равнодушии природы. Если это на самом деле так, то процессы управления могут осуществляться лишь в искусственно созданных системах. Так ли это на самом деле? Настолько ли равнодушна природа, как это следует из второго начала термодинамики?

Заметим прежде всего, что, пытаясь объяснить сущность второго начала термодинамики, мы ввели очень много различных условий. Мы совершенно не учитывали те воздействия, которым неизбежно подвергается всякая физическая система со стороны внешней среды. На элементы системы мы наложили чрезвычайно суровое ограничение, запретив им делиться на части, а также полностью исключив из рассмотрения процессы, происходящие внутри самих элементов. Наконец, мы совершенно не рассматривали влияния других законов природы, столь же всеобщих, как и второе начаао термодинамики. Посмотрим теперь, что получится, если хотя бы частично снять эти ограничения.

Начнем с последнего. Выше мы все время исходили из предположения что все возможные состояния системы равновероятны. В качестве модели такой системы мы брали мешок с карточками я настаивали на том, что карточки из мешка вытаскиваются наугад т. е. совершенно случайным образом.

Можно предложить и другую модель, более близкую к действительности - стеклянную банку, заполненную каким-нибудь газом, например водородом. Банка хорошо закупорена, а стенки ее настолько толстые, что практически теплообмен между газом и внешней средой полностью отсутствует. Газ внутри банки находится при определенной температуре. Это означает, что средняя скорость движения его молекул имеет некоторую постоянную величину. При этом каждая отдельная молекула движется с некоторой скоростью, причем данная скорость может как угодно отличаться от средней. Молекулы непрерывно сталкиваются между собой, и после каждого такого столкновения изменяются как направления движения, так и скорости каждой из двух столкнувшихся молекул.

Давайте мысленно привяжем к каждой молекуле ярлычок и напишем на нем число, равное скорости данной молекулы в данный момент времени. Полную совокупность таких чисел определим как состояние физической системы.

После каждого столкновения числа, написанные на ярлычках, придется заменять другими, и, следовательно, система непрерывно переходит из одного состояния в другое.

Если предположить, что в какой-то момент времени мы знали все числа, написанные на ярлычках, т. е. скорости движения всех молекул, то после многократных столкновений эти скорости изменятся, и если теперь мы взглянем на нашу банку с газом, каждое число, написанное на ярлычке, можно рассматривать как случайное. Казалось бы, здесь снова можно говорить о безразличии природы, которое в данном случае проявляется в том, что каждая молекула способна принимать любое значение скорости. Но на самом деле это не совсем так. Вспомним, что скорость молекулы определяет ее кинетическую энергию, а сумма энергий всех молекул составляет полную энергию газа, заключенного в банке. Выше мы сделали предположение, что обмен энергией между газом, находящимся в банке, и внешней средой отсутствует, следовательно, в силу закона сохранения энергии или, как его иначе называют, первого начала термодинамики энергия газа должна оставаться постоянной, а значит, должна оставаться постоянной и сумма скоростей отдельных молекул.

Поскольку скорость молекулы не может быть отрицательной (мы рассматриваем только абсолютные значения скоростей, а не их направления), сказанное означает, что скорость отдельной молекулы, во всяком случае, не может быть больше той суммы скоростей, которая и определяет общую энергию системы. Опять мы можем сказать, что каждая молекула в рассматриваемом примере может принимать любое из числа возможных значений скорости, причем слово "возможных" приобретает в данном случае совершенно конкретный смысл: возможных, т. е. таких, при которых не нарушается закон сохранения энергии.

Итак, мы видим, что безразличие природы не безгранично. Она безразлична лишь до тех пор, пока не нарушаются ее основные законы.

Но пойдем дальше. В примере с газом мы рассматривали молекулы как упругие шарики, которые сталкиваются между собой, а также со стенками сосуда и затем разлетаются в разные стороны, не претерпевая при этом никаких изменений, кроме изменения скорости. Но мы знаем, что каждая молекула в свою очередь представляет собой сложную систему, состоящую из нескольких атомов.

Каждый атом - это опять сложная система, состоящая из ядра и нескольких движущихся вокруг него электронов. Согласно основному принципу квантовой физики электрон в атоме не может принимать любого значения энергии, а лишь сравнительно небольшое число разрешенных значений. Кроме того, общее количество электронов в атоме должно быть таким, чтобы сумма их отрицательных зарядов уравновешивала положительный заряд ядра. Все это дополнительные ограничения, накладываемые "равнодушной" природой. o Если вернуться теперь к той же самой банке, но предположить, 1то она заполнена не чистым водородом, а смесью двух газов - водорода и кислорода, причем такой смесью, что на две части водорода приходится одна часть кислорода, да к тому же еще нагреть эту смесь до определенной температуры, то вместо безразличных столкновений и отскакиваний молекул произойдет совсем другое. Молекулы водорода начнут соединяться с молекулами кислорода, в результате чего образуется вода. Мы не рекомендуем читателю находиться вблизи такой банки, поскольку процесс соединения молекул происходит очень бурно. Попросту он сопровождается взрывом.

Но в то же время мы вынуждены констатировать, что в данном случае беспорядок сменяется относительно большим порядком. Во всяком случае пространство, вначале заполненное хаотически движущимися атомами, оказывается теперь заполненным тройками таких атомов, причем в пределах каждой тройки атомы связаны между собой в строго определенном порядке.

Еще более впечатляющая картина получится в том случае, если вместо водорода и кислорода мы возьмем два других газа, а именно пары натрия и хлор. Атомы снова начнут соединяться друг с другом, и в результате такого соединения образуются правильные кубики кристаллов поваренной соли. Здесь уже порядок выступает в настолько явном виде, что всякий, кто не знаком с кристаллами, мог бы усмотреть в подобном явлении разумную деятельность с неменьшими основаниями, чем если бы он увидел квадрат, начерченный на скале незнакомой планеты.

Попробуем разобраться, что же, собственно, происходит. В соответствии с теми же законами квантовой физики, электроны, которые могут принимать только строго определенные значения энергии, располагаются на различных расстояниях от атомного ядра. Каждому такому расстоянию соответствует то, что принято называть электронной оболочкой. На оболочке, расположенной ближе всего к ядру, могут располагаться только либо один, либо два электрона. На последующих оболочках может располагаться до восьми электронов.

Свойства атома зависят от того, сколько электронов имеется на внешней оболочке. Если их ровно восемь, вещество, состоящее из таких атомов, как говорят, химически инертно. Если же электронов на внешней оболочке меньше, чем восемь, такие атомы охотно соединяются с другими атомами, стремясь при этом образовать молекулы, у которых общая для обоих атомов внешняя оболочка содержит ровно восемь электронов. Все это хорошо известно читателю из обычного курса химии.

Однако попробуем теперь рассмотреть те же процессы под несколько другим углом зрения. Предположим на время, что атомы различных веществ просто обладали бы способностью "склеиваться" друг с другом, причем совершенно безразлично, какой атом с каким. Представим себе атомы этакими шариками, намазанными клеем.

Снова представим себе банку, наполненную такими атомами, которые к тому же находятся в непрерывном движении. Какова вероятность образования молекулы, состоящей из двух атомов, в данном месте объема банки? Если атомы - это шарики, намазанные клеем, то для образования молекулы достаточно, чтобы два атома просто оказались в нужном месте. Следовательно, искомая нами вероятность - это вероятность сложного события, сотоящего в том, что атом некоторого вещества оказался в данный момент времени в данном месте (обозначим это событие как х) и атом другого вещества оказался в тот же самый момент времени в том же самом месте (обозначим это событие как у). Вероятности сложных событий мы условились выше обозначать через р(х, у). Следовательно, р(х,у) - это вероятность образования двухатомной молекулы в случае, когда атомы представляют собой шарики, намазанные клеем. Поскольку оба наших события очевидно независимы, то р(х, у)=р(х)р(у), где р(х) - вероятность атому вещества А оказаться в данное время в данном месте, а р(у) - тоже самое для атома вещества Б.

Если, пойти теперь несколько дальше и предположить, что наша банка заполнена атомами самых различных веществ, то очевидно, что эти атомы будут соединяться в любых сочетаниях и все эти сочетания будут равновероятными, если, конечно, все атомы представляют собой шарики, намазанные клеем, и все они с равной вероятностью могут оказаться в данном месте банки.

Совсем иначе будет обстоять дело в случае настоящих атомов. Здесь для образования молекулы еще недостаточно, чтобы два атома в одно и то же время оказались в одном и том месте. Необходимо еще одно дополнительное условие, а именно, чтобы внешние оболочки встретившихся атомов определенным образом соответствовали друг другу. Молекула воды, например, образуется тогда, когда встречаются два атома водорода, во внешних оболочках которых имеется по одному электрону, и один атом кислорода, у которого во внешней оболочке нехватает как раз двух электронов. Следовательно, вероятность образования молекулы будет теперь отличаться от вероятности встречи атомов. Требуется еще дополнительное условие, чтобы встретились нужные атомы.

Теперь можно снова привлечь введенное выше понятие конфигурации. Если банка заполнена атомами кислорода и водорода, а мы знаем об этих атомах только, что они могут склеиваться по три, то в силу всех проведенных выше рассуждений мы вправе ожидать, что такие тройки атомов будут образовываться самым произвольным образом, т. е. возможны образования троек: водород-водород-водород, водород-водород-кислород, водород-кислород-кислород, кислород-кислород-кислород. Наиболее вероятной окажется конфигурация, при которой тройки каждого вида встречаются в одинаковых количествах. Мы были бы вправе утверждать даже, ссылаясь на второе начало термодинамики, что если в некоторый данный момент времени в банке имеет место другая конфигурация, то рано или поздно она обязательно уступит свое место конфигурации наиболее вероятной.

Однако опыт говорит нам о другом. Если в банке имеются атомы кислорода и водорода и если выполняются некоторые дополнительные условия, состоящие в данном случае в том, что атомы должны обладать определенным запасом кинетической энергии, то какова бы ни была исходная конфигурация, через весьма небольшой промежуток времени она уступит место другой конфигурации, а именно такой, когда каждый атом кислорода окажется соединенным с двумя атомами водорода. Только те атомы, которые оказались "лишними", могут соединяться друг с другом иным и то далеко не всяким образом.

Нужно ли делать из этого вывод, что второе начало термодинамики действует не всегда? "Конечно, нет", - ответит на такой вопрос ортодоксальный физик. Ведь из многочисленных наблюдений и опытов мы прекрасно знаем, что именно последняя из описанных конфигураций и является в рассматриваемом случае наиболее вероятной. И система "банка с кислородом и водородом" стремится при нять наиболее вероятное состояние в полном соответствии со вторым началом термодинамики.

Но тогда возникает следующий вопрос. Мы знаем и другое: если заполнить банку атомами других веществ или рассматривать ту же банку с кислородом и водородом, но при других значениях кинетической энергии атомов, то наиболее вероятными окажутся другие конфигурации. Вправе ли мы утверждать тогда, что второе начало, а может быть, и другие фундаментальные законы термодинамики проявляются по-разному в зависимости от того, что мы знаем о системе, где происходят те или иные процессы? Ну, конечно же, нет. Процессы, происходящие в природе, ни в малейшей степени не зависят от того, что мы о них знаем и не знаем. А вот сами атомы - те действительно "знают", какие конфигурации они должны образовывать в тех или иных условиях.

Следовательно, мы вправе сделать сейчас чрезвычайно важный вывод. Атомы различных веществ в силу особенностей строения их внешних электронных оболочек содержат определенное количество информации. Эта информация и позволяет отличать, например, атом водорода от атома кислорода.

Очень интересно, что информация, содержащаяся в атомах, в разных случаях используется по-разному. Человек-исследователь получает информацию косвенно, исследуя физические, химические и другие свойства веществ. К сожалению, современная техника еще не дает возможности исследователю увидеть электроны в атоме и подсчитать их количество на оболочках. Природа же использует информацию, содержащуюся в атомах, непосредственно при химических реакциях, т. е. при образовании молекул из отдельных атомов. Так или иначе, но именно информация и есть та причина, которая позволяет создавать системы, обладающие большим относительным порядком, чем тот исходный материал, из которого они создаются.

Заметим, что вообще-то говоря, мы могли и не привлекать к рассмотрению столь тонкие объекты, как атомы. Тот же самый эффект был нами уже использован однажды, когда мы предложили изготовлять карточки в мешке из двух различных материалов - железа и меди. Различие между медными и железными карточками имело тогда тот же самый смысл, что и различие, например, между атомами водорода и кислорода. В этой связи можно привести и еще один пример.

Заполним теперь наш мешок не карточками, а металлическими кубиками. Если высыпать эти кубики из мешка, то они образуют кучку, причем в пределах этой кучки кубики будут распределяться совершенно случайным образом. Если высыпать кубики на деревянную доску и продолжать встряхивать эту доску, то можно получать любые сочетания кубиков, причем все они будут равновероятны, а вероятность каждого данного сочетания представляет собой чрезвычайно малую величину.

Ситуация резко изменится, если кубики намагнитить. Тогда они начнут притягиваться друг к другу, причем к определенной стороне одного кубика будет притягиваться совершенно определенная сторона другого кубика. Если вытряхнуть такие кубики из мешка на доску и встряхивать эту доску, то вместо беспорядочного распределения будут получаться забавные узоры. Предлагалось даже использовать такие кубики для создания абстрактных скульптур.

Ясно, что здесь мы снова наблюдаем уже знакомое нам явление. Намагниченный кубик - это все равно что атом с определенной структурой внешней электронной оболочки. Он сочетается с другими кубиками не произвольно а совершенно определенным образом. Система, которая строится из таких кубиков, при желании может рассматриваться либо как абстрактная скульптура, либо как некий аналог кристаллических решеток, создаваемых природой. Кубики можно, например, намагнитить, так чтобы из них получались узоры, напоминающие снежинки.

Сделаем еще одно наблюдение. Смесь двух газов - кислорода и водорода, даже если в ней выдержаны должные пропорции, может в течение сколь угодно долгого времени оставаться такой же точно смесью и в ней не будет образовываться никаких молекул Причина этому состоит в том, что атомы самих газов кислорода и водорода также соединяются в молекулы. Молекула водорода, например, состоит из двух атомов, и их общая электронная оболочка содержит ровно два электрона. Такая молекула инертна и поэтому реакции в смеси не возникает. Если же мы нагреем хотя бы небольшой участок смеси, то под влиянием дополнительной энергии нагревания молекулы газов начнут разбиваться на отдельные атомы, а эти атомы в свою очередь начнут соединяться между собой, но уже в других сочетаниях. Поскольку реакция соединения кислорода с водородом сопровождается выделением энергии, а эта энергия в свою очередь может быть затрачена на разрыв связей других молекул, возникает так называемая цепная реакция, проще говоря, взрыв.

Все сказанное выше можно обобщить следующим образом. Для того чтобы в физической системе возник процесс, направленный в сторону достижения большего относительного порядка, необходимо, по меньшей мере, два условия. Первое из них - наличие в системе определенного количества информации. Такую информацию, как мы уже установили, несут в себе сами атомы из-за особенности структуры их внешних электронных оболочек или металлические кубики, если они намагничены. Второе условие можно назвать внешним. Для реакции образования воды в смеси кислорода с водородом таким внешним условием явилось первоначальное нагревание. В случае намагниченных кубиков внешнее условие - это встряхивание доски, на которую насыпаны кубики.

Образование более сложных и менее вероятных конфигураций требует уже не одно условие, а наличие сочетаний большого количества различных внешних условий. Так, например, если составить смесь различных веществ, углерода, водорода, азота и некоторых других и подвергнуть эту смесь воздействию совершенно определенного сочетания различных внешних условий, таких как температура, давление, электрическое поле, а также наличие специальных веществ, называемых катализаторами, то в смеси начнется процесс, приводящий к образованию чрезвычайно сложных молекул - молекул белка.

В настоящее время ученые умеют искусственно создавать такие условия и синтезировать белок. Правда, для этого понадобились чрезвычайно сложные установки, обеспечивающие получение и поддержание такого сочетания условий, которое само по себе мало вероятно. Но было время, когда подобное сочетание условий создалось естественным образом, - именно этому мы и обязаны появлению на земле живых существ и в том числе нас самих.

Молекула белка обладает замечательным свойством. Сам факт присутствия этой молекулы в смеси веществ приводит к тому, что начинают возникать другие подобные ей молекулы, точно так же как при опускании кристаллика в перенасыщенный раствор какой-нибудь соли мы вызываем, в нем процесс кристаллизации.

В свете всего сказанного выше мы способны теперь объяснить подобное явление следующим образом. Сочетание внешних условий, приведшее к созданию одной белковой молекулы, представляет собой конфигурацию, вероятность самопроизвольного образования которой чрезвычайно мала. Следовательно, такая конфигурация сама по себе содержит определенное количество информации и эта информация передается белковой молекуле. Молекула "запоминает" информацию точно таким же образом, как в цифровой вычислительной машине мы запоминали информации, записывая ее на карточках. Затем белковая молекула передает запомненную информацию окружающей ее среде, вызывая образование себе подобных. Назвав информацию, запомненную белковой молекулой, стратегией управления, мы можем закончить эту главу.

Аппетит поистине приходит во время еды. Назвав информацию, заключенную в белковой молекуле, стратегией управления, авторы получили блестящую возможность построить модель белковой молекулы, а затем заняться отысканием в этой модели все тех же датчиков, линий связи, усилителей и исполнительных механизмов. А коли так, то еще одно небольшое усилие - и можно опять вернуться к лягушкам и мамонтам, автомобилям и мылу. Но все это будет составлять предмет уже совсем другой науки, называемой бионикой. Поэтому не будем уподобляться засидевшемуся гостю и лучше всего подведем сейчас