Пятьсот миллионов чего? (Глава седьмая) [1973 Шилейко А.В., Шилейко Т.И.

- повторил Маленький принц: спросив о чем-нибудь, он не успокаивался, пока не получал ответа".

'- Три да два - пять. Пять да семь - двенадцать. Двенадцать? да три - пятнадцать. Добрый день. Пятнадцать да семь - двадцать два. Двадцать два да шесть - двадцать восемь. Некогда спичкой чиркнуть. Двадцать шесть да пять - тридцать один. Уф! Итого, стало быть, пятьсот один миллион шестьсот двадцать две тысячи семьсот тридцать один. -
Пятьсот миллионов чего?
- А? Ты еще здесь? Пятьсот миллионов... Уж не знаю, чего... У меня столько работы! Я человек серьезный, мне не до болтовни! Два да пять - семь

Этот отрывок из "Маленького принца" Сент-Экзюпери мы привели здесь потому, что нам самим необходимо срочно научиться считать. Это убедительно следует из всего того, что было сказано в предыдущей главе. Правда, кое-что мы уже умеем. В пятой главе мы научились вычислять интеграл с помощью цилиндра с золотником и брать производную с помощью еще более простого устройства, состоящего из кусочка металла, подвешенного на двух пружинках. Строго говоря, это устройство вычисляло ускорение, т. е. вторую производную по времени. Однако поскольку регулируемым параметром - интересующей нас величиной - была скорость, то отклонение грузика оказывалось пропорциональным первой производной от регулируемого параметра по времени.

Такие вычислительные устройства получили название аналоговых. Названы они так потому, что в своей работе подобные устройства используют метод аналогий. Сущность метода аналогий была хорошо известна Тому Сойеру. Чтобы подтвердить это, приведем еще один маленький отрывок, на этот раз из Марка Твена:

"Он подумал, что, пожалуй, стоило бы отыскать шарик, который он забросил, и терпеливо принялся за розыски. Но найти шарик не мог. Тогда он вернулся к тайнику, стал на то самое место, с которого бросал шарик, вынул из кармана второй шарик и бросил его в том же направлении, приговаривая:

Он заметил, куда упал шарик, побежал туда и стал искать. Должно быть, шарик упал слишком близко или слишком далеко. Том проделал то же самое еще два раза. Последняя проба удалась: шарики лежали в двух шагах друг от друга".

Интересно, как решил бы подобную задачу отдаленный потомок Тома Сойера, если бы он отправился в лес, снабженный последней моделью карманной цифровой вычислительной машины "настоящей Барлоу"? Такая машина могла бы оказать Тому массу неоценимых услуг, особенно на экзаменах в воскресной школе, но помочь найти шарик, брошенный в сторону, она бы, наверное, не смогла. Действительно, для решения подобной "баллистической" задачим - в машину необходимо ввести начальные условия, т. е. направление, в котором брошен шарик, и его начальную скорость. В принципе это, конечно, возможно, но потребовалась бы измерительная аппаратура, во много раз более сложная, чем та примитивная "вычислительная машина", которой пользовался Том. Вот она, сила аналогий!

Все это, конечно, шутка, однако над многим в коротком рассказе, который мы привели здесь, и особенно над тем, что шарик был найден только с третьей попытки, стоит серьезно задуматься. Специалист по аналоговой технике сказал бы, что с помощью своей "вычислительной машины" Том решал "краевую баллистическую задачу со случайными параметрами, используя при этом метод периодизации решений". Но не будем углубляться в терминологию. Заметим только, что аналоговая вычислительная машина, опираясь на существующие в природе аналогии, воспроизводит физический процесс именно так, как он происходит на самом деле. При этом для исследования полета шарика совсем не обязательно, как это делал Том, пользоваться другим таким же точно шариком. Можно использовать любую физическую систему, например электрическую цепь. Требуется только, чтобы процессы в выбранной физической системе описывались математическими уравнениями, которыми описывается исследуемый процесс. Отсюда и название - метод аналогий.

Выбираемая для исследования физическая система называется моделью исследуемой системы. Заметим, что процессы в модели оказываются аналогичными процессам в используемой системе лишь приблизительно по той причине, что никакие уравнения не могут описать происходящие в природе явления абсолютно точно со всеми мельчайшими подробностями. Поэтому и получаемое решение лишь приближенно соответствует истине. Не учтенные при описании, как говорят, "малые" параметры выступают здесь в роли случайных возмущений. Из-за их влияния Тому и пришлось бросать шарик три раза.

В настоящее время аналоговая вычислительная техника представляет собой мощнейшее средство для решения сложных задач, сводящихся в основном к дифференциальным уравнениям. Чрезвычайно широко используется она и во всевозможных автоматических системах. Вспомним, однако, что в предыдущей главе мы столкнулись с необходимостью определять вероятности различных явлений, а для этого, как также было установлено выше, надо уметь главным образом складывать и делить. Поэтому всех интересующихся принципом действия и возможностями аналоговых вычислительных машин мы отсылаем к специальной литературе^* и переходим к рассмотрению другого класса средств вычислительной техники - цифровых вычислительных машин.

^*(А. В. Шилейко, Основы аналоговой вычислительной техники. М., "Энергия", 1971.)

Для того чтобы представить себе принцип действия цифровой вычислительной машины, вернемся еще раз к вступлению. Странствуя по планетам, Маленький принц встретился с Деловым человеком, который считал звезды, толком не зная, что он считает и зачем ему это нужно. Это занятие роднит его с цифровой вычислительной машиной, которая также не знает, что она считает. Разовьем эту идею еще дальше. Представим себе человека, который хочет сосчитать звезды, но не хочет при этом научиться даже складывать. Тогда ему очень поможет устройство, к описанию которого мы и переходим.

Наше устройство представляет собой деревянный ящик, наполненный карточками (рис. 32). Точно такие ящики читатель наверняка встречал в каталоге любой библиотеки. На каждой карточке написан ее порядковый номер, и в ящик они сложены по номерам, т. е. первой по порядку лежит карточка номер 1, а последней - у противоположной стенки ящика - лежит карточка, например, с номером 200.

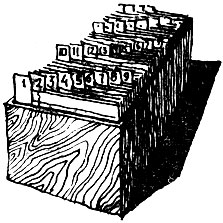
Рис. 32 Деревянный ящик, наполненный карточками

Посмотрим, как можно использовать подобное устройство для складывания чисел. Условимся, что складывать надо любые числа, состоящие не более чем из девяти цифр. Пусть, например, нужно сложить 29 783 и 37 561. Поступим следующим образом. Вытащим из ящика карточки с порядковыми номерами от 1 до 9 и запишем - на этих карточках первое слагаемое, начиная с младшей цифры. Иными словами, на карточке номер 1 напишем цифру 3, на карточке номер 2 - цифру 8 и так далее, а на карточке номер 5 - цифру 2. На карточках от номера 6 до номера 10 напишем нули.

Положим взятые карточки на место, вытащим карточки с номерами от 11 до 20 и точно таким же образом запишем на них второе слагаемое, т. е. на карточке номер 11 запишем цифру 1 и так далее, а на карточке номер 15 - цифру 3. На карточках от номера 16 по номер 20 записываем нули. Операция, которую мы только что проделали, называется вводом исходных данных.

Поставим карточки 11-20 на место и извлечем из ящика карточку номер 100. На ней написано такое правило:

Достаньте из ящика карточку номер 99 и напишите на ней с левой стороны одно под другим числа 1, 11, 21, 22 и 31. После этого выполняйте правило, написанное на следующей по порядку карточке, т. е. на карточке с номером 101.

Выполним неукоснительно все то, что предписывает это правило. Тогда карточка номер 99 приобретет вид, показанный на рис. 33. Кррме того, выполняя предыдущее правило, мы уже извлекли из ящика карточку номер 101. На ней написано:

Достаньте из ящика карточки, номера которых записаны на карточке номер 99, и разложите их в том же порядке. Затем выполняйте правило, записанное на карточке номер 102.

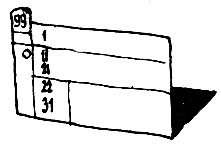
Рис. 33 Карточка номер 99 приобретет вид

Снова неукоснительно выполняем это правило, т. е. достаем из ящика карточки с номерами 1, И, 21, 22 и 31 и кладем их на стол так, чтобы сверху оказалась карточка номер 1, под ней карточка номер 11, затем карточки с номерами 21 и 22 и, наконец, в самом низу карточка номер 31. Предположим также, что на карточке номер 21 кто-то уже написал 0.

Правило, записанное на карточке номер 102, гласит:

Если на трех карточках, лежащих сверху, записаны нули, то запишите нули также и на двух остальных карточках и выполняйте правило, записанное на карточке номер 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке, т. е. на карточке номер 103.

В нашем случае явно приходится выполнять вторую часть этого правила, т. е. извлекать карточку номер 103 и выполнять то, что на ней написано. На карточке номер 103 и следующих за ней написаны такие правила:

103. Если на трех карточках, лежащих сверху, написаны цифры 1,0,0 (в любом порядке), tta четвертую сверху карточку запишите 0, а на пятую 1, после чего переходите к выполнению правила, записанного на карточке номер 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

104. Если на трех карточках, лежащих сверху, написаны цифры 1, 1, 0 или 2, 0, 0, на четвертую сверху карточку запишите 0, а на пятую 2, после чего переходите к выполнению правила, записанного на карточке номер 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

105. Если на трех карточках, лежащих сверху, написаны цифры 1,1,1, или 2,1,0, или 3,0,0 (в любом порядке), на четвертую сверху карточку запишите 0, а на пятую 3, после чего переходите к выполнению правила, записанного на карточке номер 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

106. Если на трех карточках, лежащих сверху, написаны цифры 2,1,1, или 2,2,0, или 3,1,0, или 4,0,0 (в любом порядке), на четвертую сверху карточку запишите 0, а на пятую 4, после чего переходите к выполнению правила, записанного на карточке номер 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

107. Если на трех карточках, лежащих сверху, написаны цифры 3, 1, 1, или 2, 2, 1, или 3, 2, 0, или 4, 1, 0 или 5, 0, 0 (в любом порядке), на четвертую сверху карточку запишите О, а на пятую 5, после чего переходите к выполнению правила, записанного на карточке номер 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

108. Если на трех карточках, лежащих сверху, написаны цифры 4,1,1, или 3,2,1, или 4,2,0, или 5,1,0, или 6,0,0 (в любом порядке), на четвертую сверху карточку запишите Ot а на пятую 6, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

109. Если на трех карточках, лежащих сверху, написаны цифры 5, 1, 1, или 4, 2, 1, или 3,3,1, или 7,0,0, или 5,2,0, или 4,3,0 (в любом порядке), на четвертую сверху карточку запишите 0, на пятую 7 после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

110. Если на трех карточках, лежащих сверху, написаны цифры 6, 1, 1, или 5, 2, 1, или 4, 3, 1 или 8, 0, 0, или 7, 1, 0, или 6, 2, О, или 5, 3, 0, или 4, 4, 0 (в любом порядке), на четвертую сверху карточку запишите 0, а на пятую 8, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

111. Если на трех карточках, лежащих сверху, написаны цифры 7, 1, 1, или 6, 2, 1, или 5, 3, 1, или 4, 4, 1, или 9, 0, 0, или 8, 1, О, или 7, 2, 0, или 6, 3, 0, или 5, 4, 0 (в любом порядке), на четвертую сверху карточку запишите 0, а на пятую 9, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

112. Если на трех карточках, лежащих сверху, написаны цифры 8, 1, 1, или 7, 2, 1, или 6, 3, 1, или 5, 4, 1, или 5, 5, 0, или 6, ,4, О, или 7, 3,0, или 8, 2, 0, или 9, 1, 0 (в любом порядке), на четвертую сверху карточку запишите 1, а на пятую 0, после чего переходите к выполнению правила 200. В противном случае выполняйте правивило, записанное на следующей по порядку карточке.

113. Если на трех карточках, лежащих сверху, написаны цифры 9, 1, 1, или 8, 2, 1, или 7, 3, 1, или 6, 4, 1, или 5, 5, 1, или 9, 2, О, или 8, 3, 0, или 7, 4, 0, или 6, 5, 0 (в любом порядке), на четвертую сверху карточку запишите 1, на пятую 1, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

114. Если на трех карточках, лежащих сверху, написаны цифры 9, 2, 1, или 8, 3, 1, или 7, 4, 1, или 6, 5, 1, или 9, 3, 0, или 8, 4, О, или 7, 5, 0, или 6, 6, 0 (в любом порядке), на четвертую сверху карточку запишите 1, а на пятую 2, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

115. Если на трех карточках, лежащих сверху, написаны цифры 9, 3, 1, или 8, 4, 1, или 7, 5, 1, или 6, 6, 1, или 9, 4, 0, или 8, 5, 0, или 7, 6, 0 (в любом порядке), на четвертую сверху карточку запишите 1, а на пятую 3, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

116. Если на трех карточках, лежащих сверху, написаны цифры 9, 4, 1, или 8, 5, 1, или 7, 6, 1, или 9, 5, 0, или 8, 6, 0, или 7, 7, О (в любом порядке), на четвертую сверху карточку запишите 1, а на пятую 4, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

117. Если на трех карточках, лежащих сверху, написаны цифры 9, 5, 1, или 8, 6, 1, или 7, 7, 1, или 9, 6, 0, или 8, 7Л 0 (в любом порядке), на четвертую сверху карточку запишите 1, а на пятую 5, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

118. Если на трех карточках, лежащих сверху, написаны цифры 9, 6, 1, или 8, 7, 1, или 9, 7, 0, или 8, 8, 0 (в любом порядке), на четвертую сверху карточку запишите 1, а на пятую 6, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

119. Если на трех карточках, лежащих сверху, написаны цифры 9, 7, 1, или 8, 8, 1, или 9, 8, 0 (в любом порядке); на четвертую сверху карточку запишите 1, а на пятую 7, после чего переходите к выполнению правила 200. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

120. Если на трех карточках, лежащих сверху, написаны цифры 9, 8, 1, или 9, 9, 0 (в любом порядке), на четвертую сверху карточку запишите 1, а на пятую 8, после чего переходите к выполнению правила 206. В противном случае выполняйте правило, записанное на следующей по порядку карточке.

121. Если на трех карточках, лежащих сверху, написаны цифры 9, 9, .1, на четвертую сверху карточку запишите 1, а на пятую 9, после чего переходите к выполнению правила 200.

На карточке номер 200 записано следующее сложное правило, которое для удобства мы подразделим на ряд последовательных пунктов:

а) пять карточек, лежащих на столе, положите в ящик на свои места;

б) на карточке номер 99 запишите новую колонку цифр правее предыдущей колонки так, чтобы каждая новая цифра равнялась предыдущей, увеличенной на единицу (старые цифры после этого зачеркните);

в) если новые цифры на карточке номер 99 меньше, чем 10, 20, 30 и 40 соответственно, переходите к выполнению правила, записан ного на карточке номер 101. В противном случае ваша работа завершена.

Попробуем теперь проделать все то, что нам предписывают только что сформулированные правила применительно к рассмотренному выше примеру. Перед нами на столе лежат пять карточек, на верхней из них написана цифра 3, на следующей за ней цифра 1 и затем цифра 0. Остальные две карточки пустые. Кроме того, на столе лежит карточка номер 99, на которой слева записана колонка цифр 1, 11, 21, 22, 31 (см. рис. 33).

Начинаем перебирать карточки с номерами 102-121 до тех пор, пока не дойдем до карточки номер 106. Правило, записанное на этой карточке, предписывает нам начертать на карточке, лежащей четвертой сверху (карточка номер 22), цифру 0, а на следующей за ней (карточка номер 31) - цифру 4. После этого, следуя правилу, записанному на карточке 200, мы расставляем пять лежащих перед нами карточек на свои места в ящике. Затем на карточке номер 99, которая остается лежать на столе, мы зачеркиваем 1 и пишем рядом с ней, правее, цифру 2, зачеркиваем цифру 11 и пишем правее ее цифру 12 и т. д. Карточка номер 99, после того как на ней проделано все, что предписывают правила, изображена на рис. 34.

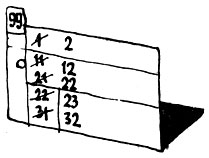
Рис. 34 Карточка номер 99, после того как на ней проделано все, что предписывают правила

Продолжаем выполнять правила. Извлекаем из ящика пять карточек с номерами 2, 12, 22, 23 и 32 и раскладываем их друг под другом. Перед нами цифры (в порядке сверху вниз) 8, 6, 0 и две пустые карточки. Это заставляет нас снова начать перебор карточек с номера 102 до тех пор, пока мы не дойдем до карточки номер 116. Выполняя записанные на ней правила, изображаем на карточке номер 23 цифру 1, а на карточке номер 32 - цифру 4. Переходим к выполнению правила, записанного на карточке номер 200, и т. д.

Если читатель не поленится довести начатый нами анализ до конца, то он убедится, что на карточках от номера 31 до номера 40 окажется записанным число 0 000 067 344. Мы записали это число так, что крайняя справа - цифра, зафиксированная на карточке номер 31, а крайняя слева - цифра, зафиксированная на карточке номер 40. Ясно также, что это число есть не что иное, как сумма чисел 29 783 и 37 561. Добавим еще, что после всего проделанного карточку номер 99 имеет смысл выбросить и заменить чистой карточкой с таким же точно номером.

То же самое следует проделать и с карточками от номера 1 по номер 40, однако уже после того, как полученный результат будет использован. Теперь наш ящик с карточками подготовлен для сложения следующей пары чисел,

Заметим, что карточки понадобились нам только для того, чтобы записывать на них или, другими словами, запоминать некоторые сведения. Поэтому ящик с карточками мы назовем запоминающим устройством или, еще короче, памятью, а отдельные карточки запоминающего устройства - ячейками.

Заметим также, что отдельные карточки в ящике использовались нами, вообще говоря, по-разному. Так, карточки от номера 1 по номер 20 можно назвать ячейками для хранения исходных данных, или условий задачи. Данные, записанные на этих карточках, нужны лишь до тех пор, пока задача не будет полностью решена. После этого их можно выбросить и. заменить пустыми с такими же номерами. К слову сказать, эта операция называется стиранием, или очищением ячеек памяти. Карточки от номера 22 по номер 30 можно назвать ячейками, хранящими промежуточные результаты вычислений. Каждая из них была нам нужна только один раз, когда складывалась соответствующая пара цифр. Поэтому здесь вместо девяти карточек можно было воспользоваться одной, зачеркивая на ней всякий раз предыдущую цифру и записывая новую, но тогда усложнились бы соответствующие правила.

Карточки с номера 31 по номер 40 называют ячейками для хранения результатрв. Эти карточки нельзя выбрасывать до тех пор, пока результат не будет тем или иным способом использован. Заметим, что результат может быть использован, в частности, и при решении следующей задачи. Тогда карточки остаются на своих местах.

Интересна роль карточки номер 21. На ней всегда записан 0. Такие карточки мы назовем ячейками, хранящими константы.

На карточке номер 99 мы записывали, зачеркивали и снова записывали цифры, которые непосредственно не участвовали в вычислениях, но использовались нами для установления порядка дейстзий. Такие карточки мы назовем рабочими ячейками.

Наконец, на карточках с номера 100 по номер 121, а также на карточке номер 200 записаны правила или, как сейчас принято говорить, программа вычислений. Читатель уже давно понял, что правила, записанные на карточках с номера 102 по номер 121, есть не что иное, как хорошо известная ему с первого класса таблица сложения. Эту таблицу, а также другие правила, позволяющие решать подчас неизмеримо более сложные задачи, принято называть алгоритмом. Алгоритм вместе с другими вспомогательными правилами, записанными в нашем случае на карточках с номерами 100, 101 и 200, и составляет программу.

Карточки с записанной на них программой играют совершенно исключительную роль. Действительно, если бы на этих карточках ничего не было записано, наша затея потеряла бы всякий смысл, так как никому не известно, что надо делать с ящиком, заполненным карточками. С другой стороны, достаточно изменить хотя бы одно правило программы, как будет решаться совершенно иная задача.

Но в рассмотренном нами примере, кроме ящика с карточками, в решении задачи принимал участие также и человек. Посмотрим подробнее, к чему сводилось это участие.

Во-первых, он должен был что-то записывать на карточках. Во-вторых, он должен был вытаскивать карточки из ящика либо по порядку, либо так, как это предписывалось правилами. Наконец, он должен был читать все, что написано на карточках, и выполнять правила. Если все организовать именно так, как было описано выше, то чтение и выполнение правил практически не требует никаких специальных знаний и способностей.

Действительно, возьмем на выбор какое-нибудь правило, например правило, записанное на карточке номер 114, и разобьем его на пункты, как это уже делалось выше. Тогда правило 114 приобретет следующий вид:

а) определите, имеются ли на трех карточках, лежащих сверху, цифры 9, 2, 1, или 8, 3, 1, или 7, 4, 1, или 6, 5, 1, или 8, 4, 0, или 7, 5, 0, или 6, 6, 0 (в любом порядке);

б) если результат, полученный при выполнении п. а), положителен на четвертую сверху карту напишите 1, а на пятую 2, после чего переходите к выполнению правила 200;

в) если результат, полученный при выполнении п. а), отрицательный, выполняйте правило, записанное на следующей по порядку карточке.

Рассмотрим сначала п. а). Ясно, что цифры, которые надо искать на трех карточках, лежащих на столе, записаны на карточке номер 114. Следовательно, действия, которые надо выполнять в соответствии с п. а), - сравнение цифр, записанных на двух различных карточках. Такое сравнение выполнить исключительно, просто, если предположить, что карточки прозрачные, а все записанные на них цифры имеют одинаковые размены и одинаковый шрифт. Тогда достаточно наложить одну карточку ца другую и посмотреть их на просвет. Автоматизировать такую операцию проще простого.

Результатом выполнения п. а) может быть только один из двух ответов - либо да, если искомая тройка цифр действительно обнаружена, либо нет - в противном случае. Каждый из этих ответов побуждает в свою очередь выполнять либо ц. б), либо п. в). Иными словами, возникает ситуация, когда в зависимости от результата выполнения первого действия осуществляется переход к выполнению либо второго, либо третьего пункта. Действие, выполняемое в подобной ситуации, называется переходом по точному совпадению. При этом совершенно неважно, что с чем совпадает, ведь вместо цифр на карточках могут быть изображены любые значки.

Пункт б) требует записать на четвертую карточку 1, а на пятую 2. Подобная операция легко может быть автоматизирована - это ясно без слов. Отметим только, что, выполняя данную операцию, мы как бы пересылаем, например, цифру 1 с карточки номер 114 на карточку, лежащую на столе четвертой сверху. Поэтому рассмотренная операция и получила название операции пересылки.

Наконец, п. в), предписывает нам вытащить карточку, стоящую в ящике следующей по порядку или, другими словами, увеличить номер предыдущей карточки на единицу. Эту операцию также чрезвычайно просто автоматизировать, если номера карточек, например, не записывать цифрами, а пробивать на карточках отверстия, количество которых совпадает с порядковым номером карточки. Тогда увеличить номер на единицу, значит, просто пробить одно дополнительное отверстие. Порядковый номер карточкой принято называть ее адресом, поэтому и сама только что рассмотренная операция получила название операции переадресации на единицу.

Снабдим наш ящик с карточками автоматом, способным выполнять три перечисленные выше операции: операцию перехода по точному совпадению, операцию пересылки и операцию переадресации на единицу. Если этот автомат работает в соответствии с еще одним правилом, а именно всегда начинает работу с просмотра карточки номер 100, то мы сможем полностью избавиться от услуг человека. Точнее, на долю человека выпадет теперь только необходимость записывать на отведенных для этого карточках исходные данные. Сам автомат, очевидно, относится к числу простейших. Согласно той классификации, которую мы провели в предыдущих главах, это автомат разомкнутого типа, выполняющий заданную раз и навсегда последовательность деислтай. Но чэдлй автомат, соединенный с ящиком, заполненным карточками, - это и есть цифровая вычислительная машина.

Чтобы устранить возможные недоразумения, торжественно заверяем читателя в том, что мы ничего не упрощали, во всяком случае в той части, которая касается принципа действия современных цифровых вычислительных машин. Цифровая вычислительная машина действительно не содержит ничего другого, кроме памяти и автомата, способного выполнять перечисленные выше операции. Если что и добавляется, так это устройства, позволяющие автоматически вводить исходные данные или извлекать результаты вычислений, но эти устройства не оказывают непосредственного влияния на процесс вычислений.

Конечно, технически все выглядит иначе. Так, память вычислительной машины - это не ящик с карточками, а устройство, состоящее из очень большого числа крохотных сердечников, способных намагничиваться и сохранять состояние намагниченности. Ряд таких сердечников составляет ячейку.Количество времени, затрачиваемого на то, чтобы записать что:нибудь в ячейку или прочесть ее содержимое, составляет у современных цифровых вычислительных машин одну десятимиллионную долю секунды. За такое же количество времени выполняются и операции перехода по точному совпадению, пересылки и переадресации на единицу. Для того чтобы выполнить сложение двух девятизначных цифр по изложенным выше правилам, современной вычислительной машине потребовалось бы около 10 мксек. Вряд ли можно предположить, что даже самый опытный и тренированный человек - вычислитель сумеет сложить два девятизначных числа быстрее чем за 10 сек. Следовательно, цифровая вычислительная машина работает примерно в миллион раз быстрее человека. Это одно из обстоятельств, объясняющих чудеса, творимые современной вычислительной техникой.

Есть и второе важное обстоятельство. Дело в том, что процесс работы по правилам, подобный описанному выше, приведет к успеху в том и только в том случае, если все правила будут выполняться неукоснительно: ни одно из них не будет пропущено и при их выполнении не будут допущены ошибки. Здесь вычислительная машина также обладает несомненными преимуществами. Современные машины могут работать без единой ошибки примерно в течение месяца. Иными словами, одна ошибка допускается за

операций. Исследования показали, что поставленный в такие же условия специально натренированный человек делает одну ошибку в среднем на каждую тысячу операций. Значит, машина ошибается в 25 920 000 000 раз реже, чем человек.

Количество ячеек в памяти современных цифровых вычислительных машин достигает нескольких миллиардов. В этой части машины пока еще уступают человеку, объем памяти которого значительно больше. Однако по мере развития технологии разрыв между объемом памяти машины и объемом памяти человека все более сокращается.

И все же наиболее поразительным, на наш взгляд, является тот факт, что каковы бы ни были быстродействие, объем памяти и надежность, самая сложная и самая совершенная цифровая вычислительная машина есть не что иное, как память, т. е. тот же самый ящик с карточками, только более усовершенствованный, и автомат, выполняющий над содержимым ячеек памяти простейшие операции.

Если память машины пуста, то она не может делать ничего, даже складывать. Все, что может цифровая вычислительная машина, это выполнять программу, записанную в соответствующих ячейках ее памяти.

С каким ликованием прочтет эти строки тот, кто до сих пор убежден, что машина лишь слепой исполнитель программы, введенной в нее человеком. Но подождите радоваться. Из всего сказанного выше с очевидностью следует, что цифровая вычислительная машина способна решить любую задачу, если только процесс решения можно описать в форме алгоритма, т. е. последовательности правил, подобной описанной выше. Составление программы - задача, которая решается также по определенным правилам. Следовательно, нет никаких препятствий к тому, чтобы машина сама составляла для себя программу. Чтобы пояснить, как это делается, вернемся еще раз к описанному выше примеру.

Заметим, что правила, начиная с записанного на карточке номер 102 вплоть до карточки с номером 121, в одинаковой мере пригодны для сложения любой пары цифр, взятых из двух слагаемых. Назовем эту часть программы стандартной программой сложения двух цифр. Правила, записанные на карточках с номерами 100, 101 и 200, обеспечивают повторение стандартной программы сложения двух цифр столько раз, сколько это нужно, пока не будет завершена операция сложения двух чисел.

Разовьем теперь эту идею дальше. Предположим, что мы хотим научить машину умножать числа. Известно, что операцию умножения можно выполнять, как ряд последовательных сложений. Следовательно, мы вправе рассматривать всю описанную нами программу как стандартную программу сложения на этот раз двух чисел. А чтобы научить машину умножать, достаточно добавить лишь несколько карточек, содержащих правила повторения стандартной программы сложения.

Но то, что получится после добавления этих карточек, это снова стандартная программа - программа умножения, а например, возведение в степень суть повторение операции умножения.

Подойдем теперь к тому же вопросу с несколько иных позиций. Перед началом работы в машине были карточки с записанными на них исходными данными задачи, в нашем примере это два числа. Но легко понять, что на карточках не обязательно писать цифры, можно писать все, что угодно, например слова, составленные из букв русского или латинского алфавита, или же какие-либо другие символы. Работа машины при этом никак не изменится, поскольку все, что делает машина, это выполнение операций сравнения. А операция сравнения будет выполнена также успешно, если на карточках, содержащих правила, будут записаны те же самые символы, что и на карточках с исходными данными. Сказанное в одинаковой степени справедливо и для настоящих вычислительных машин с памятью, состоящей из магнитных сердечников.

После выполнения программы появляются другие карточки с записанным на них результатом. Результат также не обязательно должен быть числовым, а может представлять собой последовательность любых символов, в том числе и букв, из которых составляются слова.

Рассуждая таким образом, мы можем сказать, что выполнение программы в цифровой вычислительной машине есть не что иное, как преобразование последовательности символов, представляющих собой исходные данные, в другую последовательность символов, представляющую собой результат. Заметим, что в общем случае результат может оказаться совсем не таким, которого мы ожидали.

Предположим, что мы применяем какую-то программу к некоторым исходным данным и получаем некоторый результат, не обязательно правильный. Введем меру отклонения полученного результата от правильного. В качестве такой меры можно использовать, например, количество символов в полученном результате, которые не совпадают с символами правильного результата. Предположим, наконец, что в памяти машины уже имеется большое количество разных стандартных программ, оставшихся от ранее решенных задач.

Рассмотрим теперь такую последовательность правил.

1. Применить к исходным данным некую стандартную программу (назовем ее программой А).

2. Определить меру отклонения полученного результата от правильного.

3. Изменить произвольным образом одно из правил программы А.

4. Снова применить измененную программу А к исходным данным, получить результат и определить меру отклонения нового результата от правильного.

5. Если новая мера отклонения оказалась меньше предыдущей, зафиксировать внесенное изменение и перейти к выполнению пункта 3. Если новая мера оказалась больше предыдущей, восстановить измененное правило программы А в его первоначальном виде и перейти к выполнению пункта 3.

Написанное здесь снова представляет собой программу. Выполнение этой программы может привести или не привести к успеху. В первом случае задачу можно считать решенной, причем в результате ее решения получается новая программа, т. е. машина оказывается обученной делать то, чего она раньше не умела. Если же успех не достигнут, то же самое повторяется применительно к некоторой другой стандартной программе Б и т. д. Чем больше готовых стандартных программ уже имеется в памяти машины или, другими словами, чем выше ее интеллектуальный уровень, тем больше вероятность успеха. Именно таким образом современные вычислительные машины обучаются играть в шахматы, доказывать математические теоремы и многому другому. Описанная выше программа была составлена американскими учеными Саймоном, Ньюэлом и Шоу и названа ими Всеобщим решателем задач.

Машина, снабженная Всеобщим решателем задач или любой другой эквивалентной ему программой, а также имеющая в своей памяти достаточный запас готовых стандартных программ, практически не нуждается в каком-либо дополнительном программировании. Это все же не значит, что такая вычислительная машина может действовать совершенно самостоятельно. Для выполнения работы необходимо установить цель, с которой выполняется работа. Она может быть задана либо в виде конечного результата (именно такой случай имелся в виду, когда мы рассматривали последовательность действий Всеобщего решателя задач), либо в виде определенных требований, предъявляемых к конечному результату. Интересно здесь то, что подобные требования должны быть сформулированы исключительно точно, поскольку машина будет выполнять их неукоснительно и не добавит к ним никаких дополнительных ограничений. Хорошей иллюстрацией здесь может служить анекдот, уже более десяти лет бытующий в различных вариантах в среде специалистов по вычислительной технике.

Один чрезмерно полный человек решил похудеть. Для этого надо было садиться на диету, но ему не хотелось испытывать неизбежное при диете чувство голода. Решение своей проблемы он предоставил цифровой вычислительной машине, введя в нее данные о калорийности всех имеющихся в продаже продуктов и поставив ей целью рассчитать меню, которое при заданном количестве потребляемых в день калорий обеспечивало бы максимальный общий вес продуктов. Решение, полученное машиной, оказалось простым и лаконичным: 200 л уксуса в сутки.

Чтобы избежать подобных "уксусных" решений, в последние гс ды все более четко намечается тенденция к организации для общения человека с машиной так называемого режима диалога. В режиме диалога человек не формулирует задачу сам, он только отвечает на задаваемые машиной вопросы. Вопросы же строятся в такой форме, чтобы ответами на них, по возможности, могли служить только либо да, либо нет. Таким образом, удается, во всяком случае, гарантировать достаточную полноту исходных данных и избежать "уксусных" решений, которые, очевидно, могут появиться тогда, когда предусмотрены не все возможные результаты.

Подведем итоги сказанному. Цифровая вычислительная машина во всем ее современном великолепии есть не что иное, как пустой

ящик (с карточками), соединенный с примитивным автоматом. Пока память машины пуста, она совершенно беспомощна, гораздо беспомощнее новорожденного ребенка, который с первых часов своего существования умеет уже очень многое, например сосать, глотать и переваривать пищу. Обычно при выпуске с завода память машины загружают первоначальным набором стандартных программ, позволяющих ей выполнять арифметические операции, решать многие часто встречающиеся задачи, а также стандартных программ, организующих работу первичных программ.

Дальнейшие способности машины приобретаются в результате обучения на основе накопленного опыта. Пределы такому самосовершенствованию устанавливаются только объемом памяти и, конечно, условиями, в которых протекает работа машины. Если всю свою "жизнь" машина будет решать одну и ту же задачу, например рассчитывать заработную плату, то ничего, кроме квалифицированного бухгалтера, из нее не получится. Однако если ввести в машину, например, правила игры в шашки и объяснить, что такое выигрыш, т. е. сформулировать цель, то мало-помалу такая машина может достигнуть весьма заметных результатов. Так и случилось в 1962 г., когда машина, запрограммированная американцем Артуром Л. Сэмюэлем, обыграла в шашки чемпиона штата Коннектикут Роберта В. Нили. Следовательно, в числе прочего машину можно обучить и играм, а это как раз то, что нам требуется.

Теперь мы имеем все основания составить еще одну модель автоматической системы управления. Такая модель показана на рис. 35. Располагая столь мощным средством, как цифровая вычислительная машина, мы можем представить себе теперь объект управления, значительно более сложный, чем это было до сих пор. Пусть таким объектом будет, например, завод, выпускающий много различных видов продукции. Выпуск продукции каждого отдельного вида регистрируется датчиком. Имеются также датчики, формирующие сведения о большом количестве других параметров, таких как количество имеющегося на складах и поставляемого сырья, количество поступающей к заводу энергии и т. п.

Данные от всех датчиков поступают в цифровую вычислительную машину. На основании этих данных, а также сообразуясь с заранее определенной целью, которая в нашем случае состоит в том, чтобы все виды продукции выпускались в строгом соответствии с планом и при минимальных затратах, машина разрабатывает стратегию управления и выдает сигналы, требующие применения тех или иных управляющих воздействий. Эти сигналы воспринимаются усилителями и передаются исполнительным механизмам.

Остается заметить, что введение цифровой вычислительной машины не изменило основной структуры системы управления. Снова мы имеем замкнутый контур с отрицательной обратной связью и снова система управления вводится в действие лишь тогда, когда в этом возникает необходимость, т. е. когда наблюдаются отклонения регулируемых параметров от предписанных значений. Изменились лишь количество регулируемых параметров и, конечно, сложность стратегии управления.

Познакомив читателя с основами систем автоматического управления и с принципом действия цифровых вычислительных машин, трудно обойти молчанием еще одно направление современной науки, само право которого на существование многими до сих пор ставится под сомнение. Это так называемый искусственный интеллект.

Рис. 35 Модель автоматической системы управления

Под общим названием "искусственный интеллект" объединяется сейчас целый ряд научных исследований, так или иначе связанных с попытками моделирования различных аспектов умственной деятельности человека. При этом с самого начала выделились два принципиально различных подхода к проблеме. Первый подход, сторонники которого составляют сейчас подавляющее большинство, заключается в программировании электронных цифровых вычислительных машин. Программа составляется таким образом, чтобы достигаемая в результате работа машины внешне как можно ближе напоминала работу человеческого мозга при решении сходных задач.

Второй подход основывается на изучении структуры человеческого мозга или отдельных его частей и попытках моделирования техническими средствами самой этой структуры. Поскольку о тонкой структуре мозга нам сегодня практически еще ничего не известно, совершенно естественно, что как количество сторонников этого второго подхода, так и количество выполненных в этом направлении работ насчитывает единицы.

Чрезвычайно большой интерес представляет сама история возникновения и развития рассматриваемого направления. Большинство авторов по совершенно понятным соображениям связывает начало работ в области искусственного интеллекта с появлением в 40-х годах нашего века электронных цифровых вычислительных машин. Только наиболее радикально настроенные ученые, такие, например, как уже упоминавшиеся выше Ньюэлл, Саймон и Шоу, позволяют себе говорить о предыстории и даже о доисторическом периоде исследований искусственного разума. Однако даже доисторический период они относят всего лишь на десятилетия назад, имея в виду отдельные работы по моделированию процессов мышления средствами аналоговой вычислительной техники.

На самом деле начало работ в области искусственного интеллекта следует датировать значительно более ранними сроками. Еще Лейбницем были проделаны успешные опыты по созданию механизмов, моделирующих процессы построения высказываний на основании законов формальной логики. При желании можно было бы указать примеры и более ранних работ, однако этого не стоит делать, дабы избежать бесплодных споров. В то же время нам представляется совершенно очевидным, что отмеченные опыты Лейбница имеют, возможно, даже большее право быть причисленными к области искусственного интеллекта, чем некоторые современные исследования, связанные, например, с распознаванием образов.

Тот факт, что начало исследований искусственного интеллекта следует относить не на несколько десятилетий, а, по меньшей мере, на 300 лет назад, имеет, на наш взгляд, чрезвычайно важное значение. Именно здесь кроется одно обстоятельство, во многом определившее пути развития исследований.

Разрабатывая теоретические основы кибернетики - науки, устанавливающей общность многих процессов, происходящих в живых организмах и искусственно создаваемых системах, Норберт Винер совершенно естественным образом пришел к заключению, что подобную общность следует усматривать во всем, включая также и процессы, объединяемые под названием "мышление" Винером была высказана даже мысль о возможном "бунте" машин, причем здесь имелись в виду не фантастические явления далекого будущего, а совершенно конкретные события, которые могут происходить в системах, характеризуемых высокой степенью автоматизации.

Подобные идеи Винера встретили яростное сопротивление большинства его современников. Поскольку наряду с этим нельзя было игнорировать явные успехи машин в таких, например, областях, как решение математических задач или управление артиллерийской стрельбой, и к тому же не было ни малейшей возможности отрицать тот факт, что во всяком случае решение математических ?адач - это процесс, безусловно относящийся к категории "мышление", то немедленно было предложено подразделять мыслительные процессы на "творческие" и "нетворческие". Как очень хорошо подметил один из ученых, к области разумного начали относить лишь то, чего не могут делать машины. Подобное определение обладает тем несомненным преимуществом, что оно эволюционирует по мере развития техники.

Так или иначе, но область исследований, относящихся к классу искусственного интеллекта, резко сузилась. Это не значит, конечно, что были прекращены или хотя бы сокращены работы по таким естественным применениям цифровых вычислительных машин, как решение математических задач. Но в то же время стало традицией называть искусственным интеллектом только модели различных "творческих" процессов. Мы берем здесь слово "творческих" в кавычки потому, что на сегодня не существует никакого маломальски убедительного определения, позволяющего провести различие между процессами творческими и нетворческими. Одна из попыток дать подобное определение принадлежит профессору Стенфордского университета Джону Маккарти. "Можно сказать. - говорит Маккарти, - что машина имеет интеллект, если она способна делать такие вещи, что если бы их делал человек, то мы имели бы основание считать его умным". Следуя Маккарти, мы должны определить теперь, чт такое умный человек, и проблема будет решена. Отложим пока обсуждение этого вопроса, и заметим только, что согласно общепринятой концепции человек, способный решать в уме сложнейшие математические уравнения и не более того, ни в коей мере не должен считаться умным.

Попробуем теперь разобраться, что представляют собой опыты по созданию искусственного разума, начав со второго из отмеченных выше направлений. По полу лаборатории резво катается на колесиках маленькая металлическая тележка, внешне напоминающая черепаху. На первый взгляд движения тележки кажутся совершенно беспорядочными, но присмотревшись внимательнее, можно заметить много интересного. Например, натолкнувшись на препятствие, тележка резко сворачивает в сторону, огибает его и продолжает двигаться по свободному пространству.

С течением времени движения тележки становятся все более вялыми и вдруг ее поведение резко изменяется. Вместо того чтобы беспорядочно метаться по комнате, тележка устремляется к стене и на несколько минут застывает в неподвижности у штепсельной розетки. Затем все повторяется сначала.

Неподготовленный наблюдатель вправе прийти в восторг. Действительно, бездушный механизм чувствует препятствия ч умеет их преодолевать. "Проголодавшись", он самостоятельно отыскивает кормушку (штепсельную розетку) и, подключившись к ней, насыщается (подзаряжает свои аккумуляторы). Иными словами, механизм ведет себя вполне разумно.

Уклонившись снова от обсуждения понятия "разум", укажем лишь, что для того, кто прочел предыдущие главы, в поведении черепашки нет ничего таинственного. В передней части тележки установлен бампер, при нажатии на который замыкается контакт. Контакт включает . миниатюрный электрический моторчик, поворачивающий передние колеса. Когда контакт разомкнётся, колеса поворачиваются в прежнее положение. При уменьшении напряжения аккумулятора ниже установленного предела включается чуть более сложная система управления, содержащая программу подключения к розетке.

Все это мы уже разбирали выше на большом количестве примеров, и пока такая черепашка при всей своей похожести на живое существо оказывается ничуть не сложнее швейной машины. Но вот еще один эксперимент. Экспериментатор наблюдает за черепашкой со свистком во рту и свистит каждый раз, когда черепашка наталкивается на препятствие. Проделав так несколько раз подряд, экспериментатор свистит, хотя никакого препятствия на пути черепашки нет, и - о чудо! - черепашка послушно поворачивает и катится в другом направлении. Она научилась реагировать на свисток. Установился условный рефлекс, правда, не надолго. Уже через какую-нибудь минуту черепашка перестает обращать внимание на свистки, и процесс обучения нужно начинать сначала. Моделирование условных рефлексов, моделирование процессов самообучения - это уже не работа по заданной программе.

Как же достигается такая способность черепашек? Было испробовано множество различных способов создавать самообучающиеся системы. Мы не будем описывать ни один из них, а построим свой собственный прибор, используя при этом опыт, полученный в предыдущих главах. Схема такого прибора показана на рис. 36. Главную роль в этом приборе играет та самая биметаллическая пластинка с обмоткой-подогревателем, которой мы с таким успехом пользовались в главе второй. Но начнем по порядку.

При нажатии на бампер Б замыкается контакт К. От положительного полюса аккумуляторной батареи электрический ток, проходя через замкнутый контакт К, поступает в двигатель Д рулевого управления. Через обмотки двигателя цепь тока замыкается на отрицательный полюс аккумулятора. Именно так работает черепашка, лишенная условного рефлекса.

Кроме того, при замыкании контакта К электрический ток от положительного полюса аккумуляторной батареи проходит также через обмотку реле Р₂ и возвращается к отрицательному полюсу аккумулятора. В результате замыкается контакт К₂₁ реле Р₂, но, как легко убедиться, внимательно рассмотрев схему, замыкание одного только контакта К₂₁ не влечет за собой никаких дополнительных действий.

В состав прибора входит также микрофон М. Когда раздается сильный звук, на выходе микрофона образуется электрическое напряжение. Это напряжение усиливается усилителем У (опять усилитель, на этот раз, по всей вероятности, выполненный на транзисторах) и вызывает прохождение электрического тока через обмотку реле P₁. В результате замыкаются сразу два контакта - К₁₁ и К₁₂, но, как легко убедиться, замыкание этих контактов опять-таки не вызывает никаких дальнейших действий. Заметим для определенности, что в положении, изображенном на рисунке, контакт, связанный с биметаллической пластинкой, разомкнут.

Совсем иначе будет обстоять дело, если сильный звук (свисток) раздастся в тот самый момент, когда будет нажат и бампер Б. В этом случае одновременно замкнутся оба контакта - К₁₁ и К₂₁ Электрический ток от положительного полюса аккумуляторной батареи пройдет сначала через контакт К₁₁, потом через контакт К₂₁ и, пройдя по обмотке-нагревателю биметаллической пластины, замкнется на отрицательный полюс аккумулятора. Контакты К₁₁ и К₂₁ остаются замкнутыми все время, пока свистит свисток и прижат бампер, и все это время биметаллическая пластина будет нагреваться. За один раз она нагреется не так уж сильно, но если совпадение свистка и нажатия на бампер будет повторяться много раз, пластина, наконец, нагреется настолько, что, изогнувшись, замкнет контакт, расположенный на ее конце. Если теперь не трогать бампер, а издать только громкий звук, реле Р₁ замкнет контакт К₁₂ и по цепи от положительного полюса аккумуляторной батареи через контакт K₁₂ и контакт биметаллической пластинки ток попадет в обмотки двигателя Д. Колеса повернутся. Черепашка научилась слушаться свистка. Через некоторое время биметаллическая пластина остынет, ее контакт разомкнётся и все придется начинать сначала.

Укажем теперь на одно очень важное обстоятельство. Биметаллическая пластина изгибается на нужную величину, достаточную для замыкания контактов, после нескольких импульсов тока, протекающих по ее обмотке-нагревателю. Иными словами, здесь наблюдается то же самое явление, которое мы рассматривали в главе второй в связи с датчиками и конструкцией нервной клетки, а именно явление порога срабатывания. Только после воздействия определенной силы (в нашем случае величина этой "силы" измеряется количеством импульсов тока) достигается тот или иной эффект. Оказывается, биметаллическая пластина, кроме многих полезных свойств, обнаруженных выше, позволяет также строить устройства, обладающие порогом срабатывания. Порогом срабатывания обладают и нервные клетки, что является одним из весьма важных их свойств. Многочисленные конструкторы строили своих черепашек совсем не для того, чтобы поражать воображение простаков, слабо разбирающихся в технике. Целью всех подобных экспериментов было доказать, что столь на первый взгляд сложный процесс, как обучение, можно воспроизвести, располагая лишь сравнительно простыми элементами, единственным требованием к которым является наличие порога срабатывания, будь-то нервная клетка или биметаллическая пластинка.

Некоторым из наших читателей может показаться, что слово "обучение" мы используем здесь без достаточных оснований. Чтобы развеять сомнения, рассмотрим конструкцию еще одного прибора, названного персептроном. Однако предварительно бросим еще один прощальный взгляд на рис. 36. Сделаем это для того, чтобы убедиться, что, меняя положение контакта, связанного с биметаллической пластиной, можно изменять величину порога срабатывания. Действительно, чем меньше величина зазора между контактом - и пластиной, тем меньше должна изогнуться пластина, тем меньшее количество импульсов тока потребуется для замыкания контакта. Наоборот, отдаляя контакт от пластины, можно увеличивать порог срабатывания. В дальнейшем нам будет безразлично, пользуемся мы биметаллической пластиной или каким-либо другим, может быть, менее понятным, но более простым с точки зрения современной технологии устройством. Важно лишь то, что мы располагаем элементом, обладающим порогом срабатывания, и знаем, что при желании этот порог срабатывания можно делать либо больше, либо меньше. Теперь мы полностью подготовлены для конструирова ния персептрона.

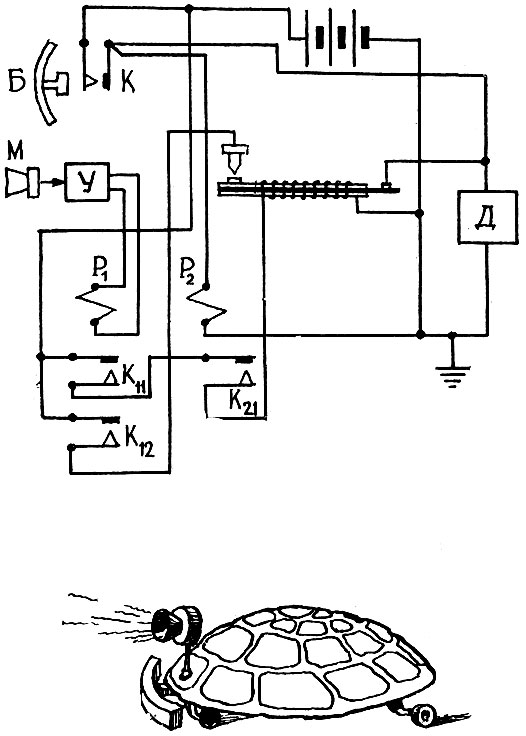
Рис. 36 Персептрон

Персептрон - это машина для распознавания образов. О тонкой структуре человеческого мозга мы знаем пока чрезвычайно мало. Поэтому в основу конструкции персептрона, которая представляла собой попытку построить модель подобной структуры, были 1 положены два ведущих соображения. Первое из них состояло в том, что мозг является совокупностью отдельных клеток, способных воспринимать и передавать возбуждение. Второе соображение сводилось к тому, что связи между отдельными клетками организуются некоторым случайным образом и в дальнейшем могут изменяться (совершенствоваться) на основе процесса обучения, т. е. последовательности актов "поощрения" и "наказания".

Эти две основные идеи нашли свое воплощение в конструкции прибора, схематически показанной на рис. 37. Персептрон состоит из трех основных частей. Первая часть, помеченная на рисунке буквой А, представляет собой прямоугольное табло, состоящее из большого количества (обычно больше 100) чувствительных органов, чаще всего фотоэлементов. Каждый чувствительный орган имеет самостоятельный вывод, на котором действует электрическое напряжение, пропорциональное интенсивности возбуждения. Если чувствительный орган - это фотоэлемент, то напряжение на его выводе пропорционально освещенности. Выводы от всех чувствительных органов соединяются с частью В.

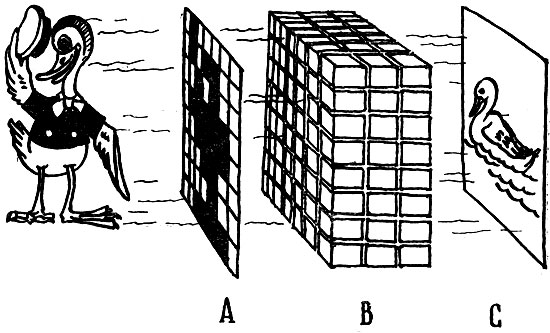
Рис. 37 Основные части персептрона

В части В прибора подсоединенные к ней выводы части А переплетаются и комбинируются между собой некоторым случайным образом. Часть В состоит из большого количества элементов, называемых обычно ассоциативными. Каждый ассоциативный элемент может находиться либо в возбужденном, либо в невозбужденном состоянии, причем переход ассоциативного элемента из невозбужденного состояния в возбужденное происходит в том случае, когда сумма сигналов, поступивших на вход этого элемента, превышает некоторый заданный уровень, называемый порогом. Сигналами, поступающими на входы ассоциативных элементов, могут быть либо выходные сигналы (электрические напряжения) чувствительных органов части Л, либо выходные сигналы других ассоциативных элементов.

Каждый ассоциативный элемент имеет выход, на котором также действует сигнал (электрическое напряжение). Выходы всех или определенной части ассоциативных элементов соединяются с частью С. Часть С также состоит из отдельных элементов, называемых реагирующими. Принцип действия реагирующих элементов в основном тот же, что и ассоциативных. Единственное отличие состоит в том, что выходы ассоциативных элементов соединяются со входами реагирующих элементов не случайно, а в некотором определенном порядке. Количество выходов реагирующих элементов также строго определено заранее и в точности соответствует количеству выбранных заранее классов распознаваемых объектов.

Пороги срабатывания ассоциативных элементов, а также в отдельных случаях и порядок соединения входов ассоциативных элементов с выходами чувствительных органов не являются постоянными, но могут изменяться под воздействием внешних сигналов, имеющих смысл поощрения и наказания. Обычно это осуществляется путем нажатия одной из двух кнопок. При нажатии кнопки поощрения существующие в части В связи и величины порогов закрепляются; при нажатии кнопки наказания величины порогов изменяются, а порядок связей (если это предусмотрено конструкцией) нарушается и заменяется другим.

Работа персептрона в свою очередь разделяется на две стадии: обучение и собственно, работа. Для обучения заранее выбирается группа объектов, каждый из которых рассматривается как типичный представитель некоторого наперед установленного класса. Один из объектов этой группы "предъявляется" персептрону, и манипулируя кнопками поощрения и наказания, добиваются такого положения, чтобы на заданном выходе части С возникал сигнал. Затем персептрону предъявляется следующий объект и т. д. Процесс повторяется много раз, поскольку при обучении распознаванию некоторого данного объекта может нарушиться уже установившаяся реакция на предыдущий объект. При удачном стечении обстоятельств персептрон оказывается способным распознавать не только объекты-представители, но и другие объекты, относящиеся к тем же классам, например одинаковые цифры или буквы, написанные по-разному или отпечатанные различными шрифтами.

Сказанное позволяет нам определить функции каждой из частей персептрона. Часть А в ответ на предъявление ей образа объекта (если чувствительные органы суть фотоэлементы, то предъявление сводится к проектированию изображения объекта на табло) вырабатывает совокупность электрических сигналов, которые можно назвать также первичными признаками. Каждому конкретному объекту соответствует своя характерная для него комбинация первичных признаков. Часть В в ответ на поступившую на входы ассоциативных элементов комбинацию первичных признаков вырабатывает свою комбинацию сигналов, которые можно назвать также вторичными признаками. Если комбинация первичных признаков зависит только от объекта, то комбинация вторичных признаков определяется как образом объекта, так и всем предшествующим процессом обучения. Часть С преобразует комбинации вторичных признаков в сигналы, указывающие на принадлежность данного объекта данному классу.

Мы столь подробно остановились на конструкции персептрона по той причине, что основные изложенные здесь идеи находят свое отражение во многих других моделях искусственного интеллекта. Каковы же результаты опытов с персептроном? Один из наиболее показательных экспериментов состоял в том, что в качестве образов, подлежащих распознаванию, персептрону предъявлялись географические карты с нанесенными на них линиями равного давления - изобарами. Цель обучения состояла в том, чтобы предсказать погоду в заданной области земного шара. После достаточно длительного обучения, а также ряда усовершенствовании, внесенных как в конструкцию персептрона, так и в методику эксперимента, были получены прогнозы, сравнимые по достоверности с прогнозами, сделанными специалистом-синоптиком. Л ведь предсказание погоды на основе карт с нанесенными на них изобарами - это однообразная работа, ежедневно выполняемая во всем мире десятками тысяч синоптиков, которые, очевидно, приобретают огромный опыт, повторяя изо дня в день одни и те же операции.

Весьма показательно, что столь впечатляющий результат не вызвал особых восторгов в среде специалистов по искусственному интеллекту. Многие авторы скорее склонны обвинять персептрон в том, что, будучи обучен отличать горизонтальные прямоугольники от вертикальных, он все же подчас путает круг с квадратом. Однако мы еще некоторое время воздержимся от выводов и перейдем пока к краткому обзору исследований, реализующих первый из отмеченных в начале главы подходов. В своем подавляющем большинстве эти исследования группируются вокруг таких направлений:

1) обучение машин различным играм и прежде всего игре в шахматы и шашки;

3) организация "диалогов", в процессе которых машина распознает смысл заданного вопроса и, если это оказывается возможным, формулирует правильный, осмысленный ответ;

6) сочинение стихов и музыкальных произведений.

Именно эти области деятельности по неким таинственным для нас соображениям принято относить к категории творческих.

К сожалению, ограниченный объем главы не позволяет нам хотя бы кратко описать используемые здесь конкретные приемы. Поэтому мы рассмотрим лишь те методы, которые в большей или меньшей степени оказываются общими для всех перечисленных задач.

Первая характерная особенность, которая определяет сам методологический подход, состоит в том, что для построения каждой модели не привлекаются какие-либо специальные технические средства. Модель во всех случаях представляет собой программу, реализуемую на цифровой вычислительной машине широкого назначения.

Хорошим примером таких программ может служить упоминавшаяся выше программа Всеобщего решателя задач. В начале этой главы мы изложили основные идеи американских ученых в несколько измененном виде применительно к рассматривавшейся там проблеме. Теперь же можно описать программу Всеобщего решателя задач именно так, как она была описана самими авторами.

Программа оперирует с четырьмя основными понятиями. Это понятия объекта, различия, оператора и цели. Понятие объекта достаточно широко. Оно включает в себя сделанное на некотором языке описание всякой конкретной ситуации, причем в число таких ситуаций могут входить как начальные (условия задачи, исходное расположение шахматных фигур на доске), так и промежуточные или же окончательные. Окончательная ситуация, как правило, представляет собой ожидаемый результат работы, т. е., например, выигрышную позицию на шахматной доске, сформулированное доказательство теоремы или законченное музыкальное произведение.

Понятие различие всегда предусматривает задание некоторой количественной меры, указывающей степень различия между какими-либо двумя объектами. Понятие оператор объединяет в себе любые средства, позволяющие преобразовать объект а в некоторый другой объект Ь.

Наиболее конкретным является понятие цели. Во Всеобщем решателе задач определены цели трех различных типов:

1) цели преобразования, состоящие в том, чтобы преобразовать объект а в объект Ь;

2) цели сокращения различия, состоящие в том, чтобы полностью уничтожить или уменьшить различие между объектами;

3) цели применения операторов, состоящие в том, чтобы применить данный оператор к некоторому объекту.

Соответственно трем видам целей имеется три различных вида процедур.

1. Процедура преобразования объекта а в объект b:

а) установи, в чем заключается различие d между объектами а и b;

г) если тебе сопутствует успех, находи новое различие и повторяй все сначала.

2. Процедура сокращения различия между объектами а и b:

а) обратись к оператору q, который может действовать в условиях различий данного вида;

б) задайся целью применить оператор q к объекту а;

г) если тебе сопутствует успех, начинай все сначала, т. е. применяй процедуру 1.

3. Процедура применения оператора q к объекту а:

а) сравни условия применения оператора со свойствами объекта а;

б) если эти условия не удовлетворяются, задайся новой целью преобразования объекта а в объект, удовлетворяющий условиям, и попытайся достичь этой цели;

в) если условия удовлетворяются, применяй оператор q к объекту с, а затем возвращайся к процедуре 2 и постарайся установить и уменьшить различия между объектом b и новым, только что полученным объектом а.

Отметим прежде всего существенное сходство только что описанных процедур с работой персептрона. Персентрон также имеет дело с объектами. Роль их играют описания распознаваемого образа (начальная ситуация) и промежуточных ситуации, в качестве которых выступают комбинации сигналов на выходах ассоциативных элементов. Каждый раз персептрои преобразует начальный объект в один из возможных промежуточных объектов. При этом фиксируются различия, которые и служат основанием для поощрения или наказания. Наконец, целью работы персептрона является преобразование заданного начального объекта в конечный объект, представляющий собой признак класса объектов.

Легко проследить, что сходные процедуры используются, например, в процессе игры в шахматы. Здесь каждый раз игрок имеет дело с объектом, представляющим собой описание позиции на доске. Операторы преобразования суть различные ходы. Цель - достигнуть выигрышной позиции.

Весьма существенное значение при реализации моделей искусственного интеллекта имеют способ организации описанных процедур и привлекаемая при выборе такого способа степень формализации. Для того чтобы сказанное стало более понятным, заметим, что, описывая каждую из трех процедур, мы использовали слово "попытайся". Это было необходимо по той причине, что, выполняя последовательность действий, предписанную процедурами, мы каждый раз неизбежно сталкиваемся с проблемой выбора. В случае игры в шахматы - это выбор одного из некоторого множества различных ходов, в случае персептроиа - выбор того ассоциативного элемента, порог которого будет изменен, и т. п. Проблема выбора сама по себе может решаться различными способами. Для подавляющего большинства ситуаций можно представить себе, во всяком случае теоретически, систему правил, однозначно определяющих выбор в каждой конкретной ситуации. Такая система правил называется алгоритмом. Если она существует и используется в действительности, сам способ организации принято называть алгоритмическим. Если же такой системы правил не существует, выбор совершается либо чисто случайным образом, либо на основе каких-то косвенных указаний. В случае шахмат, например, среди многих возможных ходов может быть испытан тот, который ранее привел к выигрышу в сходной ситуации. В подобных случаях способ организации программ принято называть эвристическим программированием. Некоторые авторы склонны даже отождествлять понятия эвристического программирования и искусственного интеллекта.

Каковы же результаты, достигнутые на пути создания программных моделей искусственного интеллекта? Сильнейшие шахматные программы в дебюте и в начале миттельшпиля играют приблизительно в силу третьего разряда, но значительно слабее в эндшпиле. Программа игры в шашки не уступает сильнейшему противнику. Добавим только, что, вероятно, можно придумать такие игры, в которых машина, вне всяких сомнений, будет оставлять человека далеко позади.

Менее чем за девять минут с помощью программы, составленной для вычислительной машины ИБМ 704, были доказаны все 350 теорем из известной книги Рассела "Principia rnathematica". Здесь интересно отметить также, что в процессе доказательства новых теорем машина использовала теоремы, доказанные ранее ею самою.

О распознавании образов говорилось уже достаточно много, добавим только, что, по мнению ряда ведущих специалистов, современные машины не только способны распознавать заболевание на основе предъявленных им перечней симптомов, но и в ряде случаев превосходят при этом опытных врачей-диагностов.

Перевод с одного языка на другой, по общему признанию специалистов, является одним из наиболее слабых мест искусственного интеллекта. Многочисленные опубликованные примеры показывают, что в этой области машины достигли лишь уровня студента первого курса технического вуза. Наконец, знаменитая "Иллиак сюита", написанная машиной для струнного квартета, может быть, и не вызывает особых восторгов, но звучит вполне "по-человечески". Во всяком случае, во время шуточного эксперимента, поставленного одним из авторов, среди двух десятков человек прослушавших "Иллиак сюиту", в число которых входили и специалисты-музыковеды, ни один не заподозрил подвоха.

Иными словами, "во внеслужебное время" машина ведет себя, как человек средних, а в некоторых случаях даже выше средних способностей. Она может узнать вас в лицо, поболтать с вами о футболе, сыграть в шахматы или в шашки, причем в шашки наверняка обыграет, поговорить на не очень правильном, но вполне понятном иностранном языке и экспромтом сложить четверостишье. Казалось бы, отсюда следует вполне естественный вывод: умственная деятельность человека допускает моделирование и сейчас весь вопрос в том, какие именно стороны этой деятельности нужно моделировать в первую очередь, чтобы принести наибольшую пользу. Примерно подобный вывод и делают специалисты. В частности, именно благодаря такому выводу работы в области искусственного интеллекта разбились сейчас на ряд самостоятельных направлений. Работы по машинному переводу привели к бурному развитию математической лингвистики, наиболее плодотворными приложениями которой являются создание специальных машинных языков и трансляторов с этих языков, дешифровка неизвестных текстов, а также весьма интересные работы по математическому анализу литературных произведений.

Работы в области распознавания образов также имеют ряд плодотворных приложений, среди которых в первую очередь нужно отметить машинную диагностику и всевозможные задачи идентификации. Опыты по организации диалогов с машиной побудили развитие одного специального направления в математике, так называемой алгебры бинарных отношений. Практическим приложением этих работ является создание специальных программ, позволяющих человеку объяснить свою задачу машине даже в том случае, если у него нет специальной подготовки в области программирования.

Однако, несмотря на целый ряд достигнутых в последние годы серьезных успехов, работы в области моделирования разумной деятельности переживают сейчас своеобразный кризис. Один из признаков этого кризиса в том и состоит, что исследования, которые еще десять лет тому назад велись единым фронтом и имели перед собой одну достаточно общую цель, разбились на ряд более мелких и подчас даже мало связанных между собой направлений. Поводом к этому послужили соображения методологического характера.

Сейчас еще трудно до конца проанализировать причины такого кризиса, а следовательно, и наметить пути его преодоления. По всей вероятности, наибольший вред принесло первоначальное деление задач на творческие и нетворческие или, выражаясь более современным языком, на алгоритмизируемые и неалгоритмизируемые. Именно в результате такого деления внимание специалистов, работающих в области искусственного интеллекта, оказалось сконцентрированным на алгоритмизируемых задачах. При этом, например, из того обстоятельства, что до сих пор не удалось создать шахматную программу, играющую в силу международного гроссмейстера, делается вывод о принципиальной невозможности моделирования творческих процессов. Иными словами, сегодня, как и четверть века тому назад, мы исходим из той основной концепции, что машина не может мыслить.

В этой связи имеет смысл вернуться сейчас к определению искусственного интеллекта, данному Джоном Маккарти. Что же должен делать человек для того, чтобы мы могли считать его умным? Один из знакомых авторов, ныне покойный, египтолог - ученый c мировым именем, член-корреспондент АН СССР, во всем, что не касалось его специальности, проявлял полнейшую интеллектуальную беспомощность. До конца своих дней он называл трамвай конкой и всегда носил в кармане записку с собственным адресом, без которой он просто не мог добраться домой. Известно также, что относительно сильный шахматист может в то же время оказаться человеком с весьма средними умственными способностями. Наконец, широко используемые на западе тесты, на основании которых определяется коэффициент интеллектуальности (IQ), в основе своей достаточно примитивны, и если применить эти тесты к машине, конечно, соответствующим образом запрограммированной, то машина заведомо получила бы высший балл.

Количество подобных примеров можно умножать до бесконечности. Единственный правильный вывод из них состоит в том, что в настоящее время мы просто не в состоянии определить понятие "умный" со степенью определенности, достаточной для того, чтобы затем можно было распространять это понятие на искусственно создаваемые модели. А коли так, то сама постановка вопроса: может ли машина мыслить? - попросту не имеет смысла. Перед тем как задавать такой вопрос, мы должны сначала строго определить понятие "мыслить", а такого определения, за исключением цитированного выше "мыслить, значит делать то, чего не может машина", пока не существует.

Все было бы очень просто, если бы сама проблема являлась чисто терминологической. Тогда можно было бы, ничтоже сумняшеся, воздать человеку человечье, а машине машинное и продолжать работы по моделированию разумной деятельности, назвав их для приличия каким-нибудь другим термином.

Но, к сожалению, дело обстоит гораздо сложнее. Общая концепция об ограниченности возможностей машинного моделирования приводит к тому, что работами в области искусственного интеллекта занимаются сейчас почти исключительно программисты. Вполне естественно, что они пользуются свойственными им приемами работы и прежде всего стремлением к математической строгости и стремлением обязательно формализовать задачу перед тем, как приступать к ее решению. За этим следует обязательное сведение условий задачи к системе правил и количественных оценок. А суть дела состоит как раз в том, что далеко не все мыслительные процессы, в том числе и достаточно примитивные, в основе своей являются формальными или хотя бы формализуемыми.

Поясним сказанное следующими примерами. Из числа фигур, изображенных на рис. 38, человек наверняка определит фигуру б как восьмерку, а фигуру г как нуль (если, конечно, заранее известно, что все эти фигуры суть цифры). В то же время машина, работающая по любому из современных методов распознавания образов, с большой степенью вероятности определит фигуру б как нуль, а фигуру г либо как восьмерку, либо вообще воздержится от распознавания. Иди другой пример. В ответ на просьбу провести на рис. 39 вертикальную линию большинство из опрошенных укажут линию АВ, в то время как машина, основываясь на системе формальных правил, конечно, всегда будет выбирать линию CD. Два перевода одного и того же литературного произведения, сделанные двумя различными переводчиками, могут одинаково хорошо передавать сущность оригинала и притом формально сколь угодно сильно отличаться друг от друга.

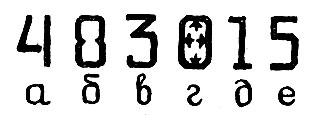
Рис. 38 Из числа фигур, изображенных на рисунке, человек наверняка определит фигуру б как восьмерку, а фигуру г как нуль

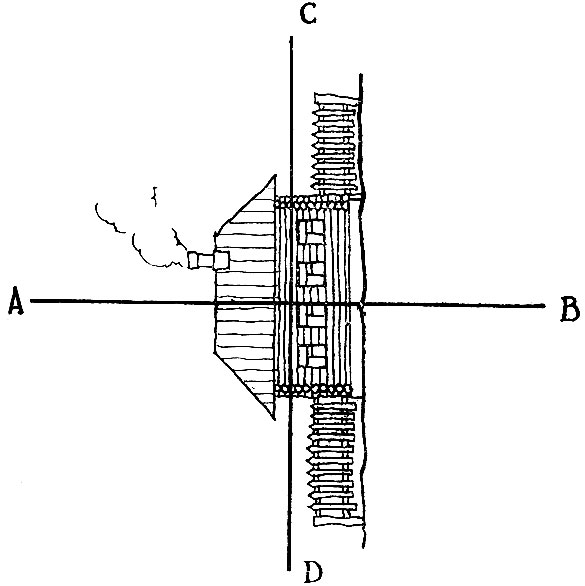
Рис. 39 В ответ на просьбу провести на рисунке вертикальную линию большинство из опрошенных укажут линию АВ, в то время как машина, основываясь на системе формальных правил, конечно, всегда будет выбирать линию CD

Все это означает, что многие мыслительные процессы в основе своей не формализуемы, во всяком случае в общепринятом смысле этого слова. Однако отсюда отнюдь не следует, что неформализуемый процесс не может быть воспроизведен в машине. Нужны просто другие методы, которые в противоположность строгим математическим методам можно назвать интуитивными. В зачаточном состоянии такие методы уже существуют, например программа игры в шашки предусматривает выбор очередного хода на основе вычисления количественных оценок различных позиций. Но наряду с этим та же программа предусматривает сравнение возникающих на доске позиций с позициями, которые имели место в ранее сыгранных машиной партиях, и может быть выбран тот самый ход, который привел к выигрышу в сходных условиях в одной из предыдущих партий. При доказательстве теорем также допускается возможность использовать ход рассуждений, уже проведенных ранее при доказательстве другой теоремы. Обобщая, можно назвать подобные приемы ассоциативным мышлением или мышлением по аналогиям.

Реализация ассоциативных приемов во многом затрудняется формальным характером самих программ, а также языков, используемых для описания ситуации. Вообще есть много оснований полагать, что проблема создания подходящего языка представляет собой в настоящее время ключ к дальнейшему развитию работ в области искусственного интеллекта.

Математические методы широко внедряются сейчас в биологию, психологию, лингвистику. Это, несомненно, приносит большую пользу, однако для дальнейшего развития работ по моделированию разумной деятельности не менее кажен, по всей вероятности, и обратный процесс, связанный с использованием при моделировании методов классической психологии или языкознания.

Рассмотрим, например, в общих чертах процесс машинного перевода. Большинство существующих программ предусматривает перевод фраза за фразой. После того как выбрана очередная фраза, в словаре отыскиваются эквиваленты всех слов, ее составляющих. Если эквивалентов для некоторого слова оказывается несколько, то они выписываются все. Затем "по контексту" отбирается наиболее подходящий эквивалент. На заключительном этапе составляется фраза перевода из отобранных слов с привлечением правил грамматики.

В качестве альтернативы к такому "строгому" методу можно предложить следующий полуфантастический прием. Пусть машина анализирует текст оригинала до тех пор, пока не станет ясно, что речь идет, например, об описании заката солнца. Затем из памяти извлекаются заранее помещенные туда, возможно, при выполнении предыдущих работ, - варианты описания солнечного заката. Из них отбирается тот, который ближе всего "совпадает с оригиналом. Затем выбранный вариант "доводится", например, путем замены эпитетов. Отличие этого приема от предыдущего состоит в том, что словарь (формальный прием) привлекается не на начальном, а на завершающем этапе работы.

Возвращаясь к вопросам методологии, можно сказать, что, по всей вероятности, было бы правильно отнести к разряду разумной деятельности любую деятельность, связанную с переработкой информации. И дело здесь опять-таки не в терминологии. Подобный взгляд попросту позволил бы создать принципиально иную основу для классификации проблем искусственного интеллекта. Появилась бы возможность подразделять задачи не на творческие и нетворческие, а по степени их сложности, понимая в данном случае под сложностью глубину привлекаемых ассоциативных связей. Что же касается методов моделирования, то в пределах каждого класса такие методы должны представлять собой разумное сочетание формальных и интуитивных приемов Необходимость в подобной или сходной с ней концепции как средстве для нового объединения усилий специалистов, работающих в области искусственного интеллекта, остро ощущается в настоящее время.

Предпочитаете заниматься совокуплением в компании прекрасной шлюхи? Портал https://prostitutkilipetskareal.info предписывает попользоваться услугами наироскошнейших индивидуалок, которые готовы даже на эксперименты в .