"Язык" машины

Помните удивительную историю с пляшущими человечками, рассказанную знаменитым Шерлоком Холмсом своему другу доктору Ватсону? Мы ее пересказывать не будем, а только приведем странные записки, которые преступник посылал своей жертве, а потом напомним конец рассказа.

Вот эти записки:

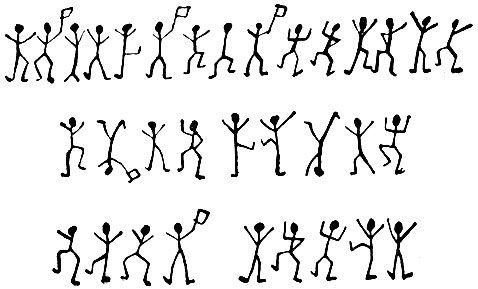
Пляшущие человечки каждому могут показаться смешными: детские рисунки, глупая забава. А вот Шерлок Холмс, хорошо знакомый с различными видами тайнописи и даже написавший небольшую статью по этому вопросу, сразу определил, что перед ним шифр. Он понял: фигурки означают буквы, и начал искать ключ.

Вскоре ключ был найден, и знаменитый сыщик постепенно вытащил из небытия одну букву за другой.

Это позволило ему не только прочитать записки, но и самому послать преступнику строчку пляшущих человечков,

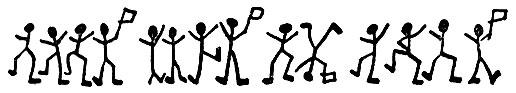
и... преступник попал в руки правосудия. Пляшущие фигурки означали слова: "Приходите сюда сейчас".

Существует много разных систем шифрования. К ним прибегают в военном деле, на дипломатической службе, вообще в тех случаях, когда нужно сохранить в тайне содержание переписки.

Шифрами пользовались и наши революционеры-подпольщики, вынужденные вести переписку так, чтобы царские жандармы не могли ее читать.

На следующей странице показан один из примеров тайнописи. Мы приводим его потому, что он тесно связан с математикой и поможет нам понять "язык" машин.

Что здесь написано? Не прочтете. Можете просидеть над шифром годы, перепробуете миллиарды комбинаций, но, не зная ключа, не прочтете! А между тем, владея им, узнать содержание зашифрованного текста не трудно.

Возьмите листок бумаги. Нарисуйте 64 шахматные клетки. Теперь вырежьте отверстия точно по рисунку. Получится решетка. Наложите ее цифрой 1 вверх на беспорядочно написанные буквы квадрата. Посмотрите: в отверстиях появился текст - электронная вычис... Теперь поверните решетку по часовой стрелке на четверть оборота. Получите следующую часть фразы: лительная машина р... Еще такой поворот: ешает сложные мате... И, наконец, при последнем повороте: матические задачи.

Не подумайте, что существует только один тип решетки, именно с 16 отверстиями, и при этом расположенными именно так, как у нас. Тогда каждый легко бы мог читать зашифрованный текст. Как число окошек, так и их расположение можно менять. Если даже оставить в решетке 16 окошек, то и тогда можно набрать невероятно большое число способов их расположения - более чем четыре миллиарда. Вот и попробуй перебери такое количество вариантов, разгадай такой шифр! Сделать это можно, только имея решетку.

Чтобы она случайно не попала в руки тех, кто стремится перехватить тайную переписку, придумали различные способы хранения решетки в памяти. Вот тут-то и помогла опять математика.

Проставим в клетках нашей решетки, там, где нет выреза, ноли, а в местах выреза - единицы.

Тогда получим восемь рядов цифр:

Первый - 01010010

Второй - 00001000

Третий - 10100010

Четвертый - 00010000

Пятый - 01000100

Шестой - 10001000

Седьмой - 00100010

Восьмой - 00010001

Запомнить расположение такого большого количества цифр, хотя они и представлены только нолем и единицей, трудно. Но здесь есть интересная закономерность, которая максимально упрощает задачу.

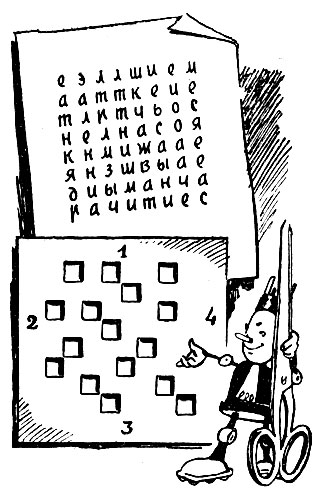
С помощью этой решетки вы прочтете, что здесь написано

Какая? Это станет понятно немного позже, после более подробного знакомства со способами кодирования.

Из примеров кодирования, о которых мы уже "рассказали, видно, что в первом случае Шерлоку Холмсу пришлось трудно. Он имел дело со множеством символов - с пляшущими человечками. Революционеры шифровали группы букв, меняя их расположение, а сама решетка кодировалась только с помощью двух символов.

А нельзя ли двумя символами кодировать и текст?

Вот ряд условных знаков: только точки и тире. Что они означают?

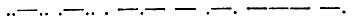
Если знаете азбуку Морзе, то прочтете слово "электро-". Значит, различные комбинации двух знаков позволили закодировать весь алфавит.

Когда вы внимательно рассматривали азбуку Морзе, то заметили, вероятно, что некоторые буквы передаются одним-двумя знаками: Е - точкой, Т - тире, А - точкой, тире, И - две точки и т. д., а другие - четырьмя и даже пятью: Ж - четыре тире, X - четыре точки, Ч - три тире, точка, Э - две точки, тире, две точки.

Двумя символами - гонкой и тире - можно записать любой текст

Попробуем определить, из скольких знаков должна состоять кодовая группа, чтобы можно было записывать все буквы одинаковым количеством, нолей и единиц.

Вначале возьмем только два знака - 0 и 1. Получим:

А=00

Б=01

В=10

Г=11

На этом наши возможности оказались исчерпаны: 2²=4. Возьмем три знака:

А=000 Д=100

Б=001 Е = 101

В=010 Ж=110

Г=011 З=111

И опять подошли к пределу - 2³=8.

Возьмем четыре знака, получим 2⁴=16. При пяти знаках, наконец, достигнем нужного результата - 2⁵=32, а это уже дает то число комбинаций, которое необходимо для кодирования всех букв в нашем алфавите.

Вот один из примеров такого кода:

Теперь подсчитаем, из скольких знаков должна состоять кодовая группа, чтобы все цифры от 0 до 9 записывать тоже одинаковым количеством нолей и единиц. И здесь оказывается, двух и трех знаков мало. А вот четырех достаточно. Они дают 16 комбинаций, а нам надо всего 10.

Вот как будут выглядеть цифры в закодированном виде:

0=0000 5=0101

1=0001 6=0110

2=0010 7=0111

3=0011 8=1000

4=0100 9=1001

Но не думайте, что эти коды алфавита и цифр единственны. Их может быть очень много - миллиарды.

Воспользуемся нашими кодами и закодируем такое слово, как "кибернетика", и число "13".

Слово будет выглядеть как группы нолей и единиц. 01001 01000 00001 00101 10000 01100 00101 10010 01000 01001 00000.

Четверично-пятеричная система счисления индейцев племени майя

Число 13 запишется так: 0001 0011.

Для записи двузначного числа понадобилось восемь знаков. Можно ли обойтись меньшим количеством знаков? Можно. Для этого только нужно изобразить число опять с помощью 0 и 1, но уже не кодовыми группами, а в двоичной системе счисления.

Мы привыкли к так называемому десятичному счислению, по которому все числа разделены на единицы, десятки, сотни, тысячи... Но есть и другие системы счисления.

От древних народов мы унаследовали, например, двенадцатиричную систему и по ней ведем счет часам и месяцам. В Англии дюжинами ведут счет в торговле, а расплачиваются по сложной денежной системе, в которой за единицу принят один пенс. Двенадцать пенсов составляют один шиллинг, а двенадцать шиллингов один фунт.

Индейцы племени майя применяли оригинальную четверично-пятиричную систему.

Число изображалось полосками и точками. Причем полоски соответствовали числу рук и ног, которыми пользовались при счете, а точки - количеству пальцев на руке или ноге.

О счете с помощью пальцев рук и ног рассказывает и выдающийся русский ученый и путешественник Миклухо-Маклай, наблюдавший жизнь туземцев Новой Гвинеи.

"Излюбленный способ счета состоит в том, - рассказывает он, - что папуас загибает один за другим пальцы руки, причем издает определенный звук, например "бе, бе, бе"... Досчитав до пяти, он говорит "ибон-бе" (рука). Затем он загибает пальцы другой руки, снова повторяет "бе, бе", пока не доходит до "ибон-али" (две руки). Затем он идет дальше, приговаривая "бе, бе", пока не доходит до "самба-бе" и "самба-али" (одна нога, две ноги). Если нужно считать дальше, папуас пользуется пальцами рук и ног кого-нибудь другого".

Существует и двоичное счисление. Оно-то чаще всего и служит "языком" машины. В нем, как мы только что узнали, есть всего два символа: ноль и единица.

Возможностями двоичного счисления люди интересуются давно. Особенно много занимались им, начиная с конца XVI века вплоть до 1780 года. Знаменитый Лейбниц тоже очень интересовался "диадической" системой (так в те времена называлась двоичная система счисления).

По его просьбе в честь двоичного счисления была даже выбита медаль. На ней изображалась таблица с числами и простейшие действия по новой системе. По краю медали на ленте было написано: "Чтобы вывести из ничтожества все, достаточно единицы".

Впоследствии в течение почти двухсот лет на эту тему не было выпущено ни одного труда. Лишь в 1931 году ученый Реймонд Вальтат продемонстрировал некоторые возможности практического применения двоичного счисления - своеобразного языка машины.

Двоичная система счисления, как и десятичная, подчинена определенным законам. Если в десятичной системе за основание числа берется величина 10, то в двоичной берется 2. Если в десятичной системе в каждом разряде может стоять одна из десяти разных цифр - от 0 до 9, - то в двоичной в каждом разряде может быть только 0 или 1. Если в десятичной системе каждый следующий разряд в 10 раз больше предыдущего, то в двоичной - каждый следующий разряд больше предыдущего в 2 раза.

Вот перед нами ряд цифр: 11111. Если считать, что это обычная десятичная запись, то единица следующего разряда в 10 раз больше единицы предыдущего. Если же принять запись по двоичной системе, то единица, стоящая на последнем - самом правом - месте, тоже обычная единица, но единица следующего разряда - на втором месте справа - уже не в 10 раз больше ее, а только в 2 и означает двойку, третья единица - четверку, четвертая - восьмерку, пятая - шестнадцать и т. д.

Желая записать какое-нибудь число, например одна тысяча семнадцать, по десятичной системе, мы разлагаем его на составные части, соответствующие разрядам этой системы. Затем производим запись: тысяч - одна (ставим единицу в разряде тысяч), сотни отсутствуют (ставим ноль в разряде сотен), десятков - один (ставим единицу в разряде десятков), единиц - семь (ставим семерку в разряде единиц). Получается запись 1017.

При записи какого-либо числа по двоичной системе мы также разлагаем его на разряды, но разряды здесь будут иные, следовательно и запись иная. Так, в числе семь: четверка - одна, двоек - одна, единиц - одна (7=4+2+1=1•2²+1•2¹+1•2⁰). Следовательно, в каждом из этих разрядов ставим по единице, получается 111. Так же поступаехМ и с другими числами.

Число десять - 10=8+2=1•2³+0•2²+1•2¹+0•2⁰; здесь отсутствуют четверки и единицы. Поэтому число десять запйсызается как 1010. Число одна тысяча семнадцать представляется так: 512+256+128+64+32+16+9+1=1•2⁹+1•2⁸+1•2⁷+1•2⁶+1•2⁵+1•2⁴+1•2³+1•2²+0•2¹+1•2⁰, и записывается в виде 1111111001.

Между прочим, и шифр рядов нашей решетки, который представлен в двоичной системе, можно, пользуясь этим правилом, перевести в десятичную. Тогда, например, первый ряд 01010010 даст 82, второй - ООЭОЮОО даст 8, третий - 10100010 - 162 и так далее.

Понятно, что ряд чисел в десятичной системе для нашей решетки 82, 8, 162, 16, 68, 136, 34, 17 запомнить не так уж трудно. А запомнив, всегда можно перевести в двоичную и по этому шифру воспроизвести решетку; там, где будут стоять единицы, вырезать окошки.

Пользоваться для кодирования двоичной системой, то есть двумя символами, очень удобно. Можно каждый знак передавать или записывать с помощью электрического тока. Например, меняя его продолжительность протекания по цепи (точка, тире - как в азбуке Морзе), или направление (плюс, минус), или амплитуду - есть сигнал, нет сигнала (единица, ноль). Последний способ применяется в электронных счетных машинах, потому что отсутствие и появление сигнала легче и надежнее всего различается в машине.

Не сразу люди пришли к мысли об использовании электрических импульсов для кодирования цифр и букв. С самого начала применения электрического тока импульсами стали управлять на расстоянии. Придумали электрический звонок. Изобретатель Иван Шильдер приспособил импульсы для взрывания мин на расстоянии.

Затем многие изобретатели в разных странах начали думать над тем, как с помощью импульсов передавать по проводам приказы, мысли. Удалось применить комбинации импульсов для передачи на расстояние кодированных цифр и букв.

Одно дело, скажет читатель, заниматься шифрованием и писать ноли и единицы на бумаге, а совсем другое - в машине. Как машина справляется с записью чисел?

Каждый видел нехитрый запор на дверях садовых калиток. Небольшая деревяшка свободно вращается на вбитом в ее середину гвозде. У такой вертушки может быть только два положения: она может либо закрыть дверь, либо открыть. Среднего положения у нее не бывает. Кроме того, вертушка может как угодно долго быть закрыта и открыта.

Садовая вертушка - приспособление чисто механическое. Его электрической аналогией будет кнопочный выключатель настольной лампы. Выключатель может быть либо включен, либо выключен. Среднего положения у него тоже не бывает. Причем выключатель будет находиться в одном из этих положений до тех пор, пока мы, нажав пальцем кнопку, не переведем его в другое. Другими словами, он неограниченно долго может фиксировать - "помнить" - включенное или выключенное состояние лампы.

По такому же принципу работают своеобразные реле, так называемые триггеры. Это устройства, с помощью которых в электронных вычислительных машинах ведется запись и счет чисел.

Упрощенно триггер можно представить в виде двух электронных ламп, смонтированных в одной колбе.

Сколько экспериментов, сколько хитроумия, сложных расчетов пришлось проделать, чтобы создать электронную лампу - эту машину электронов! В ней мельчайшие частички вещества, в сотни тысяч раз меньше атома, - электроны-лавиной срываются с раскаленной вольфрамовой нити - катода, когда через нее пропускается электрический ток. Невидимый поток электронов подчиняется строгому порядку, который создал здесь человек.

Почти абсолютная пустота в лампе - разрежение в тысячемиллиардную долю атмосферы - позволяет электронам устремляться к пластинке - аноду.

Электричеством управляют с помощью электричества. На пути электронов, между катодом и анодом, поставлена металлическая сетка. Это своеобразный регулировщик движения электронов.

Если на сетку подать достаточно большое отрицательное напряжение, она будет отталкивать от себя отрицательные электроны, поток их остановится, не достигнет анода, и лампа будет "заперта". А при запертой лампе ток через нее не протекает, напряжение на ее аноде станет высоким - порядка 50 вольт.

При положительном напряжении на сетке электроны снова начнут проскакивать через нее, привлекаемые анодом, - лампа "откроется". Через нее будет течь ток, напряжение на аноде упадет и станет равным приблизительно 5-10 вольтам.

В триггере лампы электрически соединены так, что если правая открыта, то левая обязательно будет заперта. И наоборот.

Когда правая лампа открыта, напряжение на ее аноде будет низким. Такое состояние триггера кодируется как 0. Если теперь на сетку этой лампы подать отрицательный импульс, то лампа закроется - напряжение на ее аноде быстро возрастает. Этот положительный толчок напряжения передается на сетку левой лампы, и она откроется. Триггер перейдет в другое устойчивое состояние: теперь открыта левая лампа, а на ее аноде низкое напряжение. Это состояние триггера кодируется как 1.

Каждый новый электрический импульс, поочередно подаваемый на сетки ламп, то открывает, то закрывает правую лампу. И триггер в точном соответствии с поступившим импульсом тотчас меняет свое состояние, фиксируя то единицу, то ноль.

Интересно, что в любом из двух состояний триггер, подобно выключателю, может пребывать сколь угодно долго, пока не поступит новый импульс. Следовательно, триггер может хранить - "помнить" -o? 1 или 0 до тех пор, пока это нужно, пока не поступит новый сигнал.

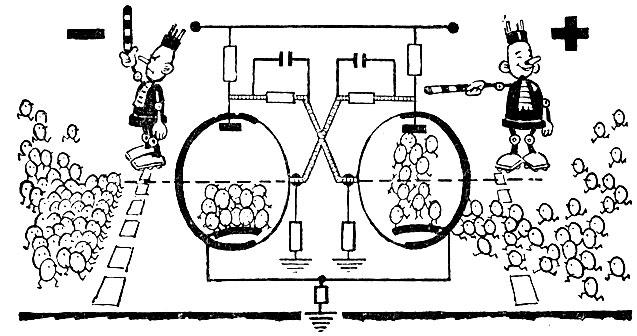
Схема триггера. Правая лампа открыта, левая закрыта - в триггере зафиксирован ноль

Так триггер, словно выключатель, переходя из одного состояния в другое, или, как говорят иногда, "опрокидываясь", позволяет отмечать импульсы.

Механическое устройство - вертушку - мы можем повернуть за 1/2 секунды, электрическое устройство выключатель срабатывает уже за 1/300 секунды, а "опрокидывание" триггеров благодаря особенностям электронных ламп происходит со сказочной быстротой - за 1/1000000 долю секунды. Как мы увидим в дальнейшем, в этом и заключается один из секретов быстроты счета электронной машины.

Триггеры как приборы счета применяются давно. У нас в стране первый триггер был создан в 1918 году известным ученым М. А. Бонч-Бруевичем.

Раньше триггеры использовали главным образом для счета атомных частиц, и лишь в последнее время они стали применяться в вычислительных машинах. Для этого их собирают в триггерные цепи-счетчики.

Вот четыре триггера, соединенных в цепь. У каждого из них по два входных и выходных контакта. Перед началом счета на всех триггерах зафиксировано состояние ноль, то есть цепь-счетчик показывает 0000.

Теперь представим, что на входные контакты первого справа триггера подан электрический сигнал - импульс. Тогда первый триггер "опрокинется" и покажет 1, а на остальных все так же будет по 0. Следовательно, цепочка триггеров зафиксирует 0001.

Передадим второй импульс. Первый триггер выключится (опять даст 0) и передаст импульс на следующий триггер. На нем зафиксируется 1. Цепь покажет 0010.

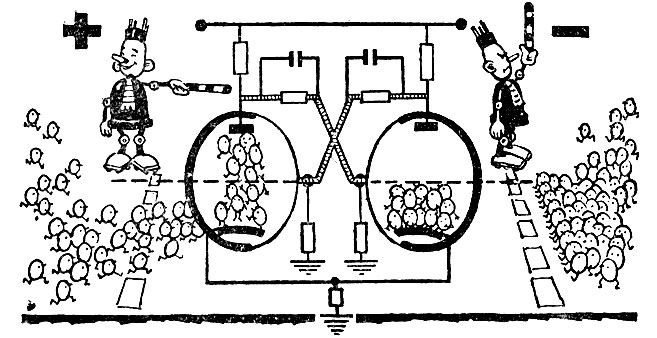
Схема триггера. Левая лампа открыта, правая закрыта - в триггере зафиксирована единица

Такую систему триггеров можно сравнить со счетами, на каждой палочке у которых всего по две костяшки. Для ведения на них счета, подобно тому как и на обычных счетах, необходимо соблюдать одно правило: когда обе костяшки данной палочки "израсходованы", передвинуты справа налево, надо передвинуть одну костяшку на следующей палочке, а эти вернуть в исходное положение.

То, что на счетах делают пальцы, в триггерах-счетчиках производят электрические импульсы.

Итак, даем третий импульс. Он снова включит первый триггер, а остальные не изменят своих положений. Теперь цепь покажет ООП.

Четвертый импульс опять "опрокинет" первый триггер и заставит его вновь дать ответный сигнал на второй триггер. Но на нем уже зафиксирована 1. Следовательно, подошедший сигнал "опрокинет" и этот триггер и включит третий. В результате цепь запишет 0100.

Продолжая наши рассуждения, получим для пятого импульса 0101, для шестого - ОНО, для седьмого - 0111, для восьмого - 1000, для девятого - 1001, для пятнадцатого - 1111.

Если сравним полученные цифры с записью в двоичной системе, то легко убедимся, что все эти сочетания нолей и единиц при переводе их с "языка машины" соответствуют числам от 0 до 15.

Как видите, здесь мы пользовались двоичной системой для записи чисел с помощью триггеров. Но такую же запись можно произвести и в десятичной системе счисления. Для этого придется каждую десятичную цифру кодировать группами нолей и единиц, как мы это делали, когда записывали число "тринадцать". Чтобы "записать" цепочкой триггеров такое двухразрядное число, понадобится восемь триггеров.

Видно, что сравнение не в пользу последнего способа: требуется уже не четыре триггера, а восемь.

Подумав, вы легко догадаетесь, как триггеры могут записывать и буквы. Ведь каждая буква - это, как мы указывали, комбинация из пяти двоичных цифр - нолей и единиц. А двоичную цифру можно записать одним триггером. Значит, для записи букв нужна цепочка из пяти триггеров.

Чтобы записать на языке машины букву В в принятом нами коде, нужно второй триггер справа поставить на 1, а оставшиеся четыре триггера на 0. Цепочка покажет 00010, то есть букву В.

Итак, цепь триггеров фиксирует и считает. Счет, как нам уже известно, идет со скоростью одного миллиона импульсов в секунду. Это в 100 тысяч раз быстрее счета, который способен вести человек.

Цена изобретения шахмат

На первый взгляд может показаться, что для подсчета больших чисел необходимо огромное количество триггерных ячеек. Здесь уместно вспомнить индийскую легенду о том, как царь Шерам предложил мудрецу Сете самому себе определить награду за изобретенную им великолепную игру. Тогда Сета положил перед царем шахматную доску и попросил, чтобы в каждую из ее 64 клеток положили пшеничные зерна, причем в первую клеточку 1, во вторую 2, в третью 4 и так в каждую последующую ровно вдвое больше, чем предыдущую.

Вначале желание мудреца показалось очень скромным. Однако мудрец своей награды так и не получил.

Математики царя Шерама подсчитали, что количество зерен выражается неподдающимся воображению гигантским числом - восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот двенадцать.

Зерно занимало бы два амбара длиной от Земли до Солнца. А ведь изобретатель шахмат сумел это число получить с помощью лишь 64 клеток.

Так и в современных электронных вычислительных машинах цепочка всего из 64 триггеров способна уже пересчитать огромное "шахматное число" - 2⁶⁴!

Как ни удивительны возможности электронных счетчиков, каждый понимает: одно дело считать импульсы, а другое - производить математические действия с числами. Но мы увидим, что и с этой задачей машина справляется довольно легко.