Бесстрастный партнер

На фоне изысканного, убранного в стиле Людовика XVI зала Тюильрийского дворца темный громоздкий ящик казался неуклюжим мещанином, неведомо какими судьбами затесавшимся в блестящий сонм аристократов.

На ящике - большая кукла, не претендующая на изящество. Перед ней шахматная доска. По другую сторону доски - Наполеон I, великий полководец и страстный любитель шахмат.

Император Франции, слывший первоклассным игроком, встретился за доской с всемирно известным... шахматным автоматом.

В зале царит торжественная тишина. Глубокое изумление, смешанное с суеверным страхом, испытывают зрители необычайного матча.

Какая сверхъестественная сила вложила в грубое подобие человека способность к тонким комбинациям, стратегическому замыслу, упорной борьбе с живым, разумным противником?

Ведь все убедились, что в ящике под куклой спрятаны лишь рычаги, валы и шестерни. Каждый собственными руками только что ощущал холод мертвых механизмов.

Долгая, напряженная борьба между человеком и безжизненной куклой закончилась поражением человека. Победил не разум, а сплетение хитроумных механизмов!

Снова и снова пытается коронованный шахматист добиться победы в борьбе со страшным в своем равнодушии партнером. Но безуспешно! С фатальной неизбежностью побеждает автомат.

Император Франции встретился со всемирно известным... шахматным автоматом

Уже много лет длится его триумфальное шествие по всем странам Европы. Тысячи людей встретились с ним за шахматной доской. Большинство терпело поражение, и лишь некоторым удавалось выиграть. Но редкие поражения не влияли на огромную популярность первой в мире шахматной машины, построенной в 1769 году венгерским механиком и изобретателем Фаркашем Кемпеленом.

"В те времена много было в стране самородных талантов, но лишь немногие из них добивались успеха, хотя бы такого, как, например, Кемпелен из Пижони. Этот мастер разъезжал от короля к королю с машиной, которая обыгрывала в шахматы любого самого сильного игрока, в том числе и самого Наполеона. До сих пор так никому и не удалось разгадать, в чем состоял секрет этой машины", - так писал о шахматном автомате и его изобретателе венгерский писатель К. Миксат в известном романе "Странный брак".

Но секрет Кемпелена был все же открыт, и совершенно неожиданно. Однажды во время демонстрации автомата в Филадельфии в городе начался большой пожар. При криках "пожар!" пришла в замешательство и машина - движения куклы стали вдруг беспорядочными. Вскоре ящик открылся... и вылез человек небольшого роста. Тщательно замаскированный шахматист с трудом выбрался из тайника, спрятанного между деталями механизмов.

Разоблаченный шахматный "автомат", много лет вводивший в заблуждение людей, прекратил свое существование. Он сгорел во время пожара, раскрывшего его тайну. Никто даже не пытался его спасти.

Кемпелену и его преемникам на редкость везло: им удавалось находить превосходных шахматных игроков маленького роста и при этом неизвестных в шахматном мире.

Первую настоящую шахматную машину построил в 1890 году испанский инженер Торрес Кеведо. Это было сравнительно простое механическое устройство, разыгрывавшее ладейный эндшпиль: король и ладья против короля. Механизм был устроен так, что ладья автомата не могла стать позади своего короля. Тем самым машина избегала пата. Она всегда выигрывала у противника, игравшего королем.

Но вот совсем недавно, несколько лет назад, любителей шахматной игры взволновало новое сенсационное известие. У шахматной доски опять появилась машина.

За шахматную доску 'села' электронная машина

Робкими и неуверенными были ее первые шаги. Как всякий начинающий игрок, машина мучительно долго "размышляла" над каждым ходом, часто "зевала", легко попадала в простые ловушки.

Нo ее "щахматнре мастерство" быстро совершенствовав лось. Прошло совсем немного времени, и необычайный шахматист - электронная вычислительная машина, говорят, уще суодела. сделать, нцчью с гроссмейстером С. Решевским.

В наши дни трудно кого-либо удивить рассказами о самых необыкновенных автоматах, даже играющих в шахматы.

"В век электроники, радио и телевидения нет нужды прятать человека внутрь шахматного автомата. Он может управлять машиной на каком угодно расстоянии. В конце концов безразлично, где находится человек, ведущий игру с помощью машины. Суть дела от этого не меняется. Ясно одно - машина сама, без помощи человека, не способна постигнуть все тонкости шахматной игры. Набор электронных ламп, проводов и механизмов не может стать равноправным членом многомиллионной ассоциации любителей шахматной игры". Так подумают многие, прочитав историю автомата Кемпелена и сообщение об успехах электронной машины на шахматном поприще.

В конечном счете это верно! За самым умным автомат том где-то всегда стоит человек.

Существует, однако, огромная разница между "автоматом" Кемпелена и современной шахматной машиной. И совсем не в том, что на смену рычагам и колесам пришли электронные лампы и провода. И не в том, что механизмом Кемпелена управлял человек, спрятанный в тайниках громоздкого ящика, а современной машиной управляет человек, сидящий в соседней комнате за большим и удобным пультом.

Принципиальное, качественное отличие заключается в том, что "автомат" Кемпелена - только механические руки, помогающие человеку передвигать фигуры на шахматной доске.

А электронная вычислительная машина - это механический "мозг", послушно выполняющий программу действия, составленную для него человеком. Играя в шахматы, машина внимательно следит за доской, "анализирует" ситуацию и самостоятельно выбирает очередной ход.

Нелегко было "посадить" электронную машину за шахматную доску. Не сразу удалось составить машинное руководство к действию для одной из самых древних и трудных игр.

Нужно было точным математическим языком описать правила игры, дать формулы, оценивающие ее ситуацию и указывающие правильный путь к победе.

В каждой игре, даже самой простой, сталкиваются противоположные интересы, каждый партнер стремится воспользоваться ошибкой противника, повернуть игру в свою пользу и добиться победы. И математика сумела проникнуть в сложный процесс борьбы, соревнования между живыми разумными существами и раскрыть, ее закономерности.

Oколо тридцати лет назад известные математики Нейман, Волд и другие создали основы математической теории игр. Она имеет большое принципиальное значение и практическое применение в экономике, военном деле и других областях. Эта теория и лежит в основе руководства к действию при "обучении" машины различным играм.

"Научить" электронную машину искусной игре в шахматы очень трудно. Но более простые игры - "В камешки" или "В крестики и цолики" - она "осваивает" быстро и проводит безошибочно.

На столе горстка камешков. Два мальчика увлечены незатейливой, но интересной игрой - кто не возьмет со стола последний камень. Правила просты. Каждый раз можно брать не больше трех камней. Выиграет тот, кто заставит партнера взять последний камень.

Игра идет с переменным успехом - случайно выигрывает то один, то другой из партнеров.

А между тем исход зависит не от случайного стечения обстоятельств, а вполне закономерен. И когда играющие в этом убеждаются, интерес сразу же пропадает. Какая же это игра, если все заранее предопределено!

Найти рбщие закономерности игры "В камешки" не так уж просто. Много тысячелетий существует национальная китайская игра "Цзяньшицзи", что в переводе означает "Выбирание камней". Играют двумя кучками камней. Каждым ходом участник мржет взять сколько угодно камней из одной кучки или по равному числу камней из обеих. Выигрывает тот, кто сумеет взять камни последним.

Оказывается, и в этой игре можно заранее точно указать исход. Математические законы игры открыты совсем недавно китайским математиком Минь Си-хао. Теперь в нее с успехом играет и машина.

В одном из павильонов научной выставки, организованной во время Британского фестиваля 1954 года, ежедневно с утра до позднего вечера царило необычайное оживление. Громкие споры, восхищенные возгласы и скептические замечания сменялись тишиной, полной напряженного ожидания.

Нетерпеливая молодежь, степенные отцы семейств и почт тецные леди с увлечением играли "В камешки" с электронной машиной "Нимрод", специально прстроенной для игры в "Ним", Она похожа на китайскую игру "Цзяньшицзи",

Камни раскладываются на произвольное число кучек. Каждый участник игры может при своем ходе брать только из одной кучки и сколько угодно камней, даже все. Выигрывает тот, кто заберет камни последним.

Машина вела игру с полным знанием дела, как самый опытный игрок. Точно выполняя руководство к действию, она одерживала одну победу за другой. Только когда исход игры с самого начала был предопределен в пользу безошибочно играющего противника, машина бесстрастно извещала о своем поражении.

О руководстве к действию - алгоритмах для решения различных задач - мы уже рассказывали в первой части книги. Теперь познакомимся с принципами алгоритмизации игр. Тогда станут понятными необычайные игровые способности вычислительной машины.

Начнем с игры "Ним". Перед нами три кучки камней. В первой - тринадцать, во второй - девять, в третьей - пять. Ход наш.

С чего же начать? Можно, например, взять один камень из любой кучки - значит, есть уже три варианта хода. Можно взять два камня тоже из любой кучки - еще три варианта, и так далее. Вариантов первого хода огромное количество. Чтобы их пересчитать, нужно много времени.

Как же выбрать первый ход и создать благоприятные для себя условия игры?

Для ответа нужно составить весь план игры. Необходимо, во-первых, четко определить все возможные ситуации, при которых предстоит сделать очередной ход. Во-вторых, нужно решить, какой выбрать ход в каждой ситуации из всех возможных вариантов.

Вот пример одного из возможных планов для игрока, начинающего игру.

Взять первым ходом все камни из первой кучки. Если противник возьмет все камни второй кучки, то вторым ходом взять оставшуюся кучку камней и выиграть. Если же противник ответным ходом возьмет 1 камень из второй кучки, то вторым ходом взять из той же кучии еще 3 камня, и в ней останется 5 камешков. Если после этого партнер возьмет 1 камень из третьей кучки (их будет 12), то своим третьим ходом взять тоже 1 камень, но из второй кучки (останется 4 камня), и так до последнего камня.

Точно так же можно построить второй, третий и последующие варианты плана. Даже для нашей простой игры с малым числом камней их существует много сотен. Эти планы игры в математике называются "стратегиями".

Чтобы правильно вести игру, каждый участник должен рассмотреть всевозможные стратегии своей игры и выбрать из них наилучшую - оптимальную. Она и должна служить ему руководством к действию.

Вряд ли кто-либо из читателей придет в восторг от такого способа обучения правильной игре - ведь составить полный перечень стратегий и выбрать из них наилучшую намного труднее, чем выбрать правильный ход в любой ситуации.

Это, безусловно, верно. И именно поэтому так трудно безошибочно проводить достаточно сложные игры.

Но оказывается, что для игры в "Ним" (или другие игры в камешки) можно обойтись без нудного перечисления всех ситуаций и анализа всех вариантов стратегии, один из которых мы пытались проделать.

Можно дать простое правило - алгоритм игры, всегда приводящий к выигрышу. Конечно, этот алгоритм не поможет, если уже в самом начале игра была безнадежной и партнер пользуется тем же правилом. Короче говоря, при игре по алгоритму ее исход предопределен начальной ситуацией.

Алгоритм игры в "Ним" особенно прост, когда числа камней в кучках представлены в двоичной системе счисления. В нашем случае числа выражаются так:

Под чертой мы выписали сумму единиц в каждом из одинаковых разрядов наших чисел. Заметьте, что в первых трех разрядах эти суммы четные - 2, 2, 0 (ноль тоже считается четным числом), а в последнем разряде сумма нечетная - 3.

Оказывается, для выигрыша нужно при каждом ходе брать столько камней, чтобы суммы единиц во всех одноименных разрядах двоичных чисел стали четными. В нашем примере этого можно достигнуть, взяв один камень из любой кучки; тогда вместо числа 2 203 останется 2 202, то есть во всех разрядах четное число единиц. Такой алгоритм обеспечивает выигрыш.

Если же к моменту очередного хода это условие уже выполнено- суммы единиц во всех разрядах четные, то ничего не попишешь - партия проиграна.

Можно, конечно, надеяться на ошибку партнера, но при опытном противнике играть дальше безнадежно.

Теперь ясно, как машина, снабженная программой, составленной по описанному алгоритму, может безошибочно играть в "Ним" при любом числе камней и кучек.

Перед очередным ходом машины в ее память вводятся данные о ситуации: число оставшихся кучек и сколько камней в каждой. Эти сведения подаются в десятичной системе счисления. Машина переведет их в двоичную систему. При сигнале "ход", машина начнет складывать числа по двоичным разрядам.

Если получится нечетная сумма единиц в каком-либо из разрядов, машина напечатает свой очередной ход: "Снять столько-то камней из кучки такой-то".

Если же все суммы окажутся четными, то в зависимости от программы машина либо напечатает "сдаюсь", либо будет продолжать игру в расчете на ошибку партнера.

Кто из нас в детстве не увлекался игрою "В крестики и нолики"?! На переменах, а иногда, чего греха таить, и во время урока на листке бумаги с девятью квадратами разыгрывались самые ожесточенные сражения. Кому удавалось поставить подряд три своих значка - тот побеждал. Но чаще всего игра заканчивалась ничьей. Партнеры быстро постигали немудреный секрет.

Чтобы электронную вычислительную машину приобщить к этой игре, нужно перевести на машинный язык ситуацию игры - положение на игровом поле. Для этого проще всего пустой квадрат обозначить 00, квадрат, в котором стоит крестик, -10, квадрате ноликом - 01.

Тогда положению в игре, изображенному на рисунке, соответствует код - 101000, 000100, 000001 - всего 18 двоичных цифр.

Теперь машина должна получить руководство к действию. Его, как и для игры "В камешки", можно задать разными способами: либо в виде оптимальных стратегий, либо просто таблицами вариантов игры.

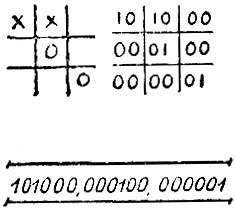
Ситуация игры перед ходом машины

Оказывается, для этой простой игры существует несколько серий вариантов. Подсчитано, что в каждой серии 512 вариантов по четыре хода. Играя по любому из этих вариантов, машина не проиграет. А если ее партнер невнимателен, то 360 вариантов приведут к выигрышу.

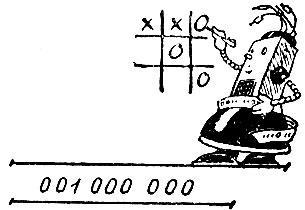
Машина сообщила свой очередной ход

В машине таблицы вариантов хранятся в "памяти". В каждой ячейке стоит код положения на игровом поле и код очередного хода. Для его обозначения достаточно всего девять двоичных цифр - по одной на каждый квадрат. Из них восемь нолей и одна единица. Ее место в ряду цифр показывает тот квадрат, куда машина должна поставить свой знак.

Предположим, что в положении, показанном на рисунке, машина должна сделать очередной ход. Она играет ноликами, и по одному из вариантов игры его нужно поставить в верхний правый квадрат. Как же машина найдет ход?

В одной из ячеек памяти хранится ряд двоичных цифр: 101000, 000100, 000001, 001, 000, 000. Первые 18 цифр показывают положение в игре, а последние 9 - очередной ход. А весь ряд означает: "При положении, изображенном на рисунке, поставить нолик в верхний правый квадрат".

В машинной игре код положения подается в сумматор. В нашем случае вводится число-101000, 000100, 000001, 000, 000, 000. Машина начинает сравнивать его с числами в ячейках "памяти". Сравнение производится вычитанием из них кода положения в игре. Когда образуется положительная разность в последних 9 разрядах, определится код следующего хода. В нашем случае это выглядит так: 101000 000100, 00001, 001, 000, 000 - 101000, 000100, 000001, 000, 000, 000 = 000000, 000000, 000000, 001, 000, 000.

Разность, равная 001, 000, 000, означает - поставить нолик в верхний правый квадрат. Этот ход машина напечатает на бумаге или просигнализирует на комплекте из 9 лампочек.

Как видите, в принципе все очень просто - дело сводится к выбору наилучшего варианта хода из большого числа возможных.

Но за простотой кроются немалые технические трудности. Чтобы вложить в машину 512 вариантов по четыре хода, приходится занять 2048 ячеек (512X4=2048). Кроме того, в "память" нужно еще поместить программу.

А это значит - всей оперативной "памяти" большой электронной вычислительной машины "Стрела" едва-едва хватает для немудреной игры на 9 квадратах.

Вернемся снова к шахматам. После знакомства с принципами механизации простых игр можно представить себе те огромные трудности, которые возникают при "обучении" машины квалифицированной шахматной игре.

В теории игр доказывается, что исход шахматной партии, как и в игре "В крестики и нолики", предрешен тем, кто делает первый ход, и выбором стратегии каждого из партнеров. И если бы удалось довести до конца решение шахматной игры - составить перечень всех стратегий и выявить оптимальные, то древняя игра потеряла бы свою привлекательность.

Как ни парадоксально, наше увлечение шахматами зиждется на том, что мы "не умеем" правильно играть - не знаем математического решения этой игры.

Бельгийский математик М. Крайчик попытался хотя бы приблизительно подсчитать общее число всевозможных вариантов шахматных партий. Оно оказалось равным 2.10116. Такое число оставляет далеко позади легендарное количество пшеничных зерен, испрошенных в награду за изобретение шахмат.

Если бы все население земного шара круглые сутки играло в шахматы, делая ежесекундно по одному ходу, то потребовалось бы не менее 10100 веков, чтобы переиграть все варианты шахматных партий.

Любители шахматной игры могут не беспокоиться. Составить список всех стратегий - решить до конца задачу шахматной игры - ближайшим поколениям не удастся даже с помощью самых быстродействующих машин. Шахматам пока не угрожает участь "Цзяньшицзи" и "Нима".

Как же при таких условиях составить руководство к действию для машинной игры?

Оно строится на системе правил, позволяющих в каждой ситуации выбрать очередной ход. Эта система правил является тактикой игры.

Чаще всего тактика строится на оценке значимости каждой фигуры. Оценка выражается числом очков. Вот таблица одной из систем оценок, принятых для шахматной игры.

Король + 200 очков Пешка + 1 очко

Ферзь + 9 очков Отсталая пешка + 0,5 очка

Ладья + 5 очков Изолированная пешка + 0,5 очка

Слон + 3 очка

Конь + 3 очка Сдвоенная пешка + 0,5 очка

Определенным образом оцениваются также позиционные качества - подвижность фигур, расположение на доске, защищенность.

С помощью чисел можно дать общую оценку своей позиции и позиции противника. Отношение общего числа очков позиции белых к числу очков позиции черных характеризует ситуацию игры. Если оно больше единицы, преимущество на стороне белых, если меньше - более выгодное положение у черных.

Предположим, машина играет черными и должна сделать очередной ход. В ее "памяти" хранится положение на доске и отношение чисел очков для этой ситуации. Выбирая ход, машина начинает вычислять изменение этого отношения при различных вариантах. Ход, ведущий к максимальному изменению отношения в пользу машины, и будет ее выбором. Машина напечатает его на карточке.

Описанная тактика - решение одноходовых задач, приведет, конечно, к очень плохой и неинтересной игре. Гораздо лучше строить игру на расчете нескольких ходов вперед. Лучшие шахматисты умеют рассчитывать комбинации вперед на 10 и более ходов.

Машина тоже может играть с выбором комбинации на несколько ходов вперед в предположении, что противник будет отвечать тоже наилучшими ходами. Но ее возможности ограничены скоростью работы и емкостью памяти.

Если считать, что на обдумывание хода нельзя тратить больше чем 15 минут, то самая быстродействующая машина может планировать игру не более чем на три-четыре хода. При огромном превосходстве над человеком в скорости вычисления машина пока не может с ним соревноваться в скорости игры за шахматной доской. Ведь ей приходится добросовестно пересчитать почти все возможные варианты, даже те, которые человек сразу же отбрасывает. Например, для решения двуходовой задачи машине пришлось выполнить 450 тысяч вычислительных операций.

Вот партия, сыгранная машиной (белые) с человеком (черные):

В этой проигрышной для белых (машина) позиции партия была прервана.

Как видите, машина-шахматист оказалась не на высоте. Но это одна из первых партий.

Вычислительная техника быстрыми шагами идет вперед. Совершенствуются методы программирования. Уже сейчас электронная вычислительная машина решает самые трудные шахматные задачи и очень недурно играет в шашки.

Можно не сомневаться, что электронный партнер скоро "научится" гораздо лучше играть и в шахматы.

Естественно, возникает вопрос, что произойдет, если "посадить" за шахматную доску две машины? Могут ли они вступить в единоборство, и кто из них выйдет победителем?

Конечно, могут! Машины прекрасно "поймут" друг друга, и каждый из этих бесстрастных партнеров будет упорно добиваться победы. Она достанется тому, кто обладает более совершенным руководством к действию, большей "памятью" и быстрее "соображает", то есть быстрее вычисляет.

Оценивая перспективы машинной игры в шахматы, чемпион мира М. Ботвинник сказал: "В будущем машина должна превзойти гроссмейстера. Тогда, очевидно, будут происходить два первенства мира: одно - среди гроссмейстеров, другое - среди машин".

Игры, о которых мы рассказывали, характерны тем, что их исход не зависит от случая. Но для многих игр дело обстоит не так.

Взять хотя бы домино. Многие к нему неравнодушны и посвящают "забиванию козла" часы досуга. Или разнообразные карточные игры. Ведь их результат определяется не только ходами участников, но и "везением". Пришла хорошая карта, и выигрыш почти гарантирован. А при плохой карте самая совершенная игра мало поможет.

Можно ли приобщить электронную вычислительную машину к подобным играм? Как составить руководство к действию, учитывающее неизбежную случайность?

Машина оказалась неплохим партнером

Оказывается, и в таких играх машина "не ударит лицом в грязь". Недавно электронная машина "Стрела" в перерыве между работой "сыграла" свою первую партию в домино. Человек и машина играли против двух человек. И, надо сказать, партнер машины не имел оснований к недовольству своим напарником. А противники очень быстро убедились, что машина играет, как самый опытный любитель, хотя и не сопровождает свои ходы мощными ударами костяшек об стол. Партию выиграли человек и машина.

Машинная игра в домино и карты тоже базируется на оптимальной стратегии. Но она, конечно, не обеспечивает в таких играх вполне закономерный результат. Руководство к действию направлено на повышение вероятности благоприятного исхода. Р.ешение задач в играх со случайными ходами производится аналогично играм с предрешенным исходом, но с привлечением законов теории вероятностей.

Существуют игры, исход которых вообще не зависит от ходов участников. Они целиком строятся на случае. К таким играм относятся, например, лото и рулетка. Для них не существует ни стратегии, ни руководства к действию. Машина, как и человек, должна здесь играть наугад.

"Однако Смок Белью нашел оптимальную стратегию для игры в рулетку и нанес серьезное поражение содержателю игорных притонов", - скажет читатель, вспоминая историю, рассказанную в первой части книги.

Совершенно верно! Но стратегия Смока базировалась на неисправной работе колеса рулетки. Это заметил Смок и стратегию своей игры построил на наилучшем использовании возникшей закономерности.

Однако он прекрасно знал, что его стратегия непригодна для исправной рулетки, и поэтому упорно отказывался играть за другим столом.

В заключение расскажем об игре, в которой машина оказалась более сильным противником, чем человек. Это хорошо известная игра "Чет-нечет". Смысл игры заключается в следующем: один из участников пишет какое-нибудь число, другой, не глядя на него, угадывает, четное оно или нечетное. Если угадал, то выиграл, если нет - проиграл.

Каждый из участников может играть по любой стратегии - оптимальной здесь не существует. Стратегия может заключаться в том, например, чтобы всегда называть "чет". Но противник очень быстро разгадает такую "чистую" стратегию партнера и начнет систематически выигрывать. Поэтому каждый старается самым незакономерным способом чередовать свои ходы.

И если два человека будут очень долго играть в эту игру, то в среднем окажется, что в 50 процентах случаев выиграет один и в 50 - выиграет другой партнер. Исход большого числа игр будет ничейным.

А игра с машиной привела к другому, неожиданному результату. Запоминая все предшествующие ходы, машина устанавливает некоторую закономерность в случайных ходах человека, которой он бессознательно пользуется. Например, он чаще называет "чет", чем "нечет", или часто после двух ходов "нечет" делает три хода "чет" и так далее.

Раскрыв это, машина вычисляет вероятность того или другого очередного хода и выигрывает чаще, чем человек.

Оказалось, из большого числа игр машина уже в 55 процентах случаев, а не в 50 процентах, заканчивает партию в свою пользу.

Там, где царит не разум, а холодный расчет, побеждает бесстрастный автомат.