§ 3. Пример математической модели

В этом параграфе на примере задачи из курса физики 9-го класса мы продемонстрируем один из распространенных методов построения математических моделей.

Задача. Тело движется прямолинейно с ускорением а м/с² и начальной скоростью ν м/с. Требуется определить, какой путь пройдет тело за Т секунд.

Тело движется

Вы знаете ответ к этой задаче:

Приведенное соотношение неоднократно проверялось в различных физических экспериментах, в том числе и вами в лабораторных работах по физике. Но, как вы хорошо знаете, всякий физический эксперимент обязательно содержит ошибки измерений. Поэтому совершенно точно формулу (1) проверить экспериментально невозможно. А чтобы вывести ее теоретически, на уроках физики, по сути дела, строилась приближенная математическая модель равноускоренного движения (хотя слово "модель", конечно, не употреблялось). Нетрудно убедиться в том, что эта модель основана на следующем допущении (см. учебник по физике для 9-го класса):

если интервал времени разбит на очень большое количество равных маленьких промежутков, то мы не сильно ошибемся, предполагая, что скорость тела на каждом из них постоянна (т. е. движение равномерно) и меняется "мгновенно" в конце каждого промежутка.

Принято считать, что при неограниченном увеличении числа отрезков разбиения мы получим величину перемещения с любой точностью. Фактически это еще одно предположение, которое лежит в основе модели, приводящей к формуле (1). Выполняя лабораторную работу 2, вы с помощью ЭВМ убедитесь в том, что чем мельче отрезки разбиения, тем ближе будет результат к значению, полученному по формуле (1).

Руководствуясь схемой, описанной в предыдущем параграфе, определим, что считать исходными данными и результатами нашей модели. Ясно, что исходными являются начальная скорость ν, ускорение а, время движения Г. Результатом, конечно, будет перемещение S.

Теперь наша цель - получить математическое соотношение, связывающее исходные данные и результат. Оно будет зависеть от того, на сколько частей мы разобьем интервал времени.

Разобьем интервал времени от 0 до Г секунд на N равных частей. Величина каждой части составляет r = T/N секунд. По нашему предположению скорость тела в течение каждого из этих промежутков времени считается постоянной. В течение первых г секунд тело движется с начальной скоростью v₁ = v м/с. На следующем отрезке (от r секунд до 2r секунд) - со скоростью v₂ = v₁+ar м/с. В течение третьего промежутка времени скорость будет равна v₃=v₂ + ar м/с. Как видите, последовательность v₁ v₂ v … является арифметической прогрессией с первым членом v и разностью d = ar. Найдем путь, пройденный телом:

Воспользуемся формулой для суммы N членов арифметической прогрессии:

Раскрывая скобки и подставляя T/N вместо r, получим:

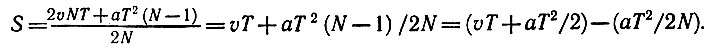
Эта формула и является математическим соотношением, связывающим исходные данные и результат. Построение математической модели закончено. Вы видите, что полученная формула для S отличается от формулы (1) слагаемым - aT²/2N, которое показывает, с какой степенью точности построенная модель описывает равноускоренное движение.

Остальные два этапа решения задачи (создание алгоритма, составление программы и анализ расчетов на ЭВМ) вы осуществите во время лабораторной работы.

Задания для самостоятельного выполнения

1. Завершите составление математической модели, начатое при решении задачи 6 к предыдущему параграфу.

2*. Выполняя утреннюю зарядку, школьник подошел к стене, на которой был закреплен пружинный эспандер, и оттянул его на некоторое расстояние (рис. 1). Какую работу совершила при этом сила натяжения пружины?

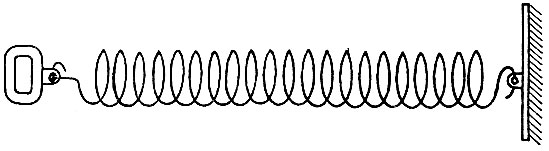
Рис. 1. Пружинный эспандер

При построении математической модели для этой задачи были сделаны следующие предположения: сила натяжения пружины подчинена закону Гука; если весь промежуток движения тела разбить на большое число равных маленьких промежутков, то можно считать, что сила на каждом из них постоянна и меняется "мгновенно" в конце каждого промежутка; при неограниченном увеличении числа этих промежутков величина работы получается с любой точностью.

Завершите построение математической додели.

3*. Составьте математическую модель для решения следующей задачи.

Плотина прямоугольной формы перегораживает реку (рис. 2). Определить силу давления воды на плотину.

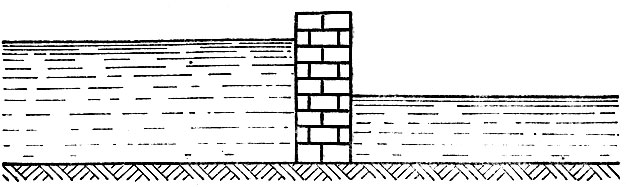
Рис. 2. Плотина прямоугольной формы

4*. Школьник, не знающий теоремы Пифагора, составил следующую математическую модель для определения длины диагонали произвольного прямоугольного стола.

Предположение: поверхность стола считаем прямоугольником; длина диагонали приближенно равна длине ломаной, изображенной на рисунке 3, если, конечно, ступени у этой ломаной достаточно маленькие; при неограниченном увеличении числа ступенек величина диагонали получается с любой точностью.

Исходные данные: длины сторон стола а и b.

Результат: длина диагонали d.

Связь между исходными данными и результатом: d = a + b (действительно, длина ломаной в точности равна а + b независимо от того, сколько в ней ступенек).

Почему получился неверный результат: диагональ прямоугольника равна сумме его смежных сторон?

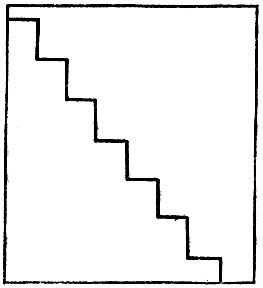
Рис. 3. Поверхность стола считаем прямоугольником