§ 7. Ветвления

Легко и просто было бы жить (и даже неинтересно), если бы удалось раз и навсегда расписать, какие поступки и в какой последовательности совершать. На самом деле нам постоянно приходится принимать решения в зависимости от создавшейся ситуации. Если идет дождь, то мы надеваем плащ. Если жарко, то идем купаться. Разумеется, встречаются и более сложные положения, когда надо сделать выбор. Давайте рассмотрим два примера.

Пример 1. Допустим, вы собрались пойти в кинотеатр на сеанс 12.00. Алгоритм покупки билетов может выглядеть так:

 Подойти к кассе. 
 Если билеты на сеанс 12.00 имеются, то купить билеты. 
 Отойти от кассы.

Пример 2. Представьте себе, что вам нужно проехать к автозаправочной станции (АЗС) по дороге, участок которой ремонтировался, и вам неизвестно, закончился ли ремонт. Подъезжая к этому участку, вы будете вынуждены воспользоваться следующим алгоритмом:

 Уменьшить скорость.

Если ремонт участка закончен, то проехать 5 км по отремонтированному участку, иначе проехать 10 км в объезд.

 Остановиться у АЗС.

"Билеты на сеанс 12.00 имеются" - это условие, которое надо проверить в первом примере. Во втором примере проверяется условие "ремонт участка закончен".

Что же происходит после проверки условия? В первом примере, если условие выполнено, совершается действие

 купить билеты,

а затем - действие

 отойти от кассы.

Если же условие не выполнено, то сразу совершается действие

 отойти от кассы.

Во втором примере в случае выполнения условия совершается действие

 проехать 5 км по отремонтированному участку,

а затем - действие

 остановиться у АЗС.

В противном случае совершается действие

 проехать 10 км в объезд,

а затем - действие

 остановиться у АЗС.

Мы видим, что при выполнении каждого из этих алгоритмов наступает такой момент, когда появляется несколько направлений для продолжения. Алгоритм как бы раздваивается, разветвляется (словно дорога). В этом случае говорят, что алгоритм содержит ветвление.

В рассмотренных ветвлениях как "прямой путь", так и "объезд" содержит только одно действие. Но так

Только ветвление поможет в сложных условиях сделать выбор

бывает далеко не всегда. Скажем, в первом примере слова "Купить билеты" предполагают выполнение нескольких действий, например, таких: протянуть кассиру деньги, назвать сеанс и количество билетов, получить билеты. Учитывая это, попробуем записать алгоритм покупки билетов более подробно. Как и раньше, будем записывать действия в столбик:

 Подойти к кассе. 
 Если билеты на сеанс 12.00 имеются, то: 
 Протянуть кассиру деньги. 
 Назвать сеанс и количество билетов. 
 Получить билеты. 
 Отойти от кассы.

Казалось бы, все в порядке: мы лишь разъяснили, что значит "купить билеты". Но по этой записи стало невозможно понять очередность выполнения действий, поскольку неясно, какое именно действие следует выполнять, если билетов на сеанс 12.00 нет. Значит, в записи алгоритма необходим специальный указатель, показывающий последнее действие, участвующее в ветвлении. Договоримся в качестве такого указателя употреблять слова "Конец ветвления" и писать его в строке, следующей за последним действием ветвления:

Указатель "Конец ветвления" лучшее средство от двусмысленности!

 Подойти к кассе. 
 Если билеты на сеанс 12.00 имеются, то: 
 Протянуть кассиру деньги. 
 Назвать сеанс и количество билетов. 
 Получить билеты. 
 Конец ветвления. 
 Отойти от кассы.

Теперь ясно: если условие не выполнено, то сразу совершается действие, записанное после слов "Конец ветвления".

Ветвления в алгоритмах записывают одним из следующих двух способов.

Первый способ:

Если Q, то:

 P1 
 Р2 
 … 
 Рn 
 Иначе: 
 Т1 
 Т2 
 … 
 Тm 
 Конец ветвления.

Второй способ:

 Если Q, то: 
 P1 
 Р2 
 … 
 Рn 
 Конец ветвления.

Здесь Q -условие, Р₁, Р₂, ..., Р_n - действия, которые совершаются в случае выполнения условия Q (первая ветвь ветвления), а Т₁ Т₂, ..., Т_m - действия, которые совершаются, если это условие не выполнено (вторая ветвь ветвления). Первый из этих способов записи называется ветвлением в полной форме, второй - ветвлением в неполной форме.

Правда, договорившись, как оформлять ветвления в алгоритмах, мы должны быть уверены в том, что исполнители сумеют исполнить такие алгоритмы. Мы уже говорили, что любой исполнитель снабжен специальным устройством управления, которое "воспринимает" алгоритмы и организует их исполнение. Будем считать, что все устройства управления "понимают" и ветвления, и вообще любые формы организации действий, о которых речь пойдет далее.

Как же исполнители воспринимают алгоритмы с ветвлениями? Встретив в алгоритме ветвление, устройство управления исполнителя проверяет, выполняется ли условие, и в зависимости от этого дает команду на выполнение одной из последовательностей действий Р₁, Р₂, ..., Р_n или Т₁, Т₂, ..., Т_m. Как только исполнитель совершил выбранную последовательность действий, ветвление заканчивается, т. е. исполнение алгоритма продолжается с действия, следующего за словами "Конец ветвления".

Любое ли условие можно записывать в качестве Q? Конечно, нет! Исполнитель должен уметь проверять, выполняется ли это условие. Иными словами, проверка условия должна быть допустимым действием исполнителя. Например, бессмысленно включать в алгоритм подготовки к экзамену такое ветвление:

 Если завтра попадется билет № 13, то: 
 Учить билет № 13. 
 Конец ветвления.

(Не пользовался ли кто-нибудь из вас подобным алгоритмом?) Очевидно, что пока вы не можете составлять разветвляющиеся алгоритмы для ЧЕРТЕЖНИКА: набор его допустимых действий не содержит проверок какого-либо условия. По той же причине нельзя составить разветвляющийся алгоритм для ВЫЧИСЛИТЕЛЯ, используя только известные вам действия "Запросить", "Сообщить" и "Присвоить".

Итак, ветвление (развилка) - это такая форма организации действий, при которой в зависимости от выполнения или невыполнения некоторого условия совершается либо одна, либо другая последовательность действий.

Чтобы более наглядно представлять те или иные формы организации действий, очень полезны так называемые блок-схемы. Каждое действие алгоритма, кроме проверки условия, будем помещать в прямоугольник, а вопрос о том, выполняется ли некоторое условие,- в ромб. Блок-схемы на рисунках 13, а, б, в, изображают соответственно последовательное выполнение действий, ветвления в полной и неполной формах. На рисунке 14 изображена блок-схема алгоритма покупки билетов.

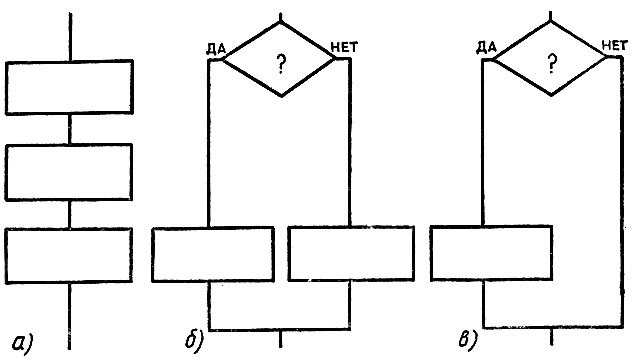
Рис. 13. Блок схемы

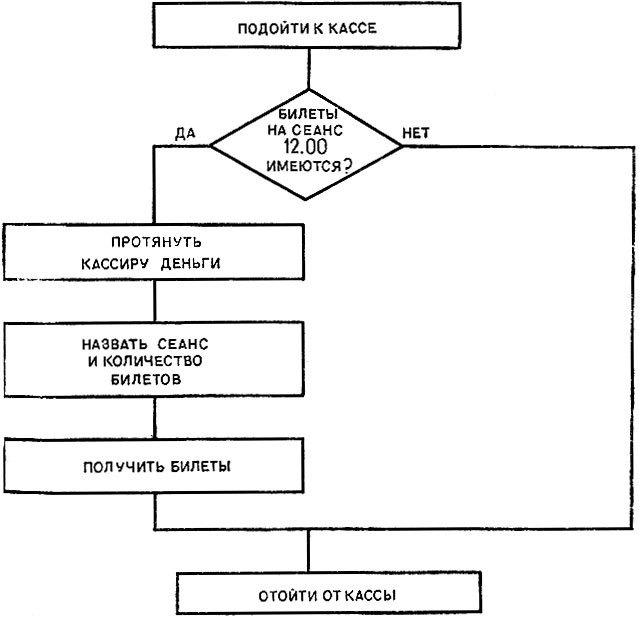
Рис. 14. Блок схема алгоритма покупки билетов

На рисунке 15 изображена блок-схема алгоритма поездки на АЗС.

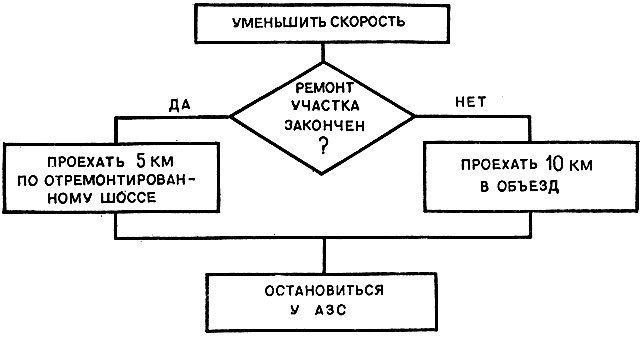
Рис. 15. Блок схема поездки на АЗС

Вопросы

1. Какие алгоритмы называются линейными?

2. Какая форма организации действий называется ветвлением?

3. Как оформляются в алгоритмах ветвления:

а) в неполной форме;

б) в полной форме?

4. Для чего служит указатель "Конец ветвления"?

5. Почему ВЫЧИСЛИТЕЛЬ и ЧЕРТЕЖНИК могут выполнять только линейные алгоритмы?

6. Как изображаются с помощью блок-схем:

а) линейные алгоритмы;

б) ветвления в неполной форме;

в) ветвления в полной форме?

Задания для самостоятельного выполнения

1. а) Проснувшись утром, школьник почувствовал недомогание. Находившийся рядом злоумышленник тут же составил для него следующий алгоритм:

 Измерить температуру. 
 Если температура выше 37°, то: 
 Вызвать врача. 
 Пойти в школу.

Несмотря на недомогание, школьник исправил этот алгоритм, добавив всего две строки. Какие строки добавил школьник?

б) Однажды школьник решил из своего дома позвонить приятелю. Злоумышленник, который и на этот раз оказался рядом, предложил ему следующий алгоритм:

 Подойти к телефону. 
 Снять трубку. 
 Набрать номер. 
 Подождать 6 секунд. 
 Если знакомый ответит, то: 
 Сказать: "Здравствуй!" 
 Сообщить последние новости. 
 Узнать, что нового и как жизнь. 
 Сказать: "До свидания!" 
 Положить трубку. 
 Конец ветвления. 
 Отойти от телефона.

Школьник воспользовался этим алгоритмом, и через некоторое время у него отключили телефон. Объясните почему.

2. Для решения каких задач предназначены следующие алгоритмы? Укажите, какие условия в них проверяются, какие действия совершаются, если условия выполнены, и какие - если условия не выполнены. Нарисуйте блок-схемы этих алгоритмов.

а)

 Присвоить х значение суммы углов А и С четырехугольника ABCD. 
 Присвоить у значение суммы углов В и D четырехугольника ABCD. 
 Если х = у, то: 
 Построить серединный перпендикуляр к отрезку АВ. 
 Построить серединный перпендикуляр к отрезку ВС. 
 Найти пересечение построенных перпендикуляров. 
 Иначе: 
 Сообщить "Построение невозможно". 
 Конец ветвления.

б)

 Присвоить х значение суммы сторон АВ и CD четырехугольника ABCD. 
 Присвоить у значение суммы сторон ВС и AD четырехугольника ABCD. 
 Если х = у то: 
 Построить биссектрису угла А. 
 Построить биссектрису угла В. 
 Найти пересечение построенных биссектрис. 
 Иначе: 
 Сообщить "Построение невозможно". 
 Конец ветвления.

3. Запишите в виде алгоритмов правила определения знака:

а) произведения двух действительных чисел;

б) суммы двух действительных чисел.

4. Составьте алгоритм размена суммы денег (k копеек):

а) двух- и трехкопеечными монетами;

б) двух- и пятикопеечными монетами;

в) трех- и пятикопеечными монетами.

5. Составьте математическую модель и алгоритм работы автомата "Газированная вода".