§ 8. Ветвления и исполнители алгоритмов

Мы уже отмечали, что, используя действия ВЫЧИСЛИТЕЛЯ "Запросить", "Сообщить", "Присвоить", нечего и пытаться составить для него разветвляющийся алгоритм: среди этих действий нет проверок условий. А ведь в реальной жизни постоянно возникают вычислительные задачи, при решении которых надо проверять те или иные условия. Какие же условия обычно приходится проверять? Конечно, эти условия связаны со сравнением чисел. Поэтому будем считать, что ВЫЧИСЛИТЕЛЬ "умеет" сравнивать числа, т. е. проверять, выполняется ли для двух чисел заданное соотношение (<, >, =, ≠, <, >).

Теперь, используя сравнение чисел, мы можем записывать ветвления для ВЫЧИСЛИТЕЛЯ, например:

 Если а<b, то: 
 Присвоить с значение а. 
 Иначе: 
 Присвоить с значение b. 
 Конец ветвления. 
 Сообщить с.

Легко понять, что этот алгоритм служит для определения наименьшего из двух чисел а и b.

Еще пример. Составим для ВЫЧИСЛИТЕЛЯ алгоритм нахождения значения функции |sin х|. ВЫЧИСЛИТЕЛЬ должен запросить у нас число х, вычислить значение у, равное sin x, а затем, если y<0, присвоить у значение - у.

 Запросить х. 
 Присвоить у значение sin x. 
 Если y<0, то: 
 Присвоить у значение - у. 
 Конец ветвления. 
 Сообщить у.

Обратимся теперь ко второму нашему исполнителю - ЧЕРТЕЖНИКУ. Раньше мы предполагали, что он движется по неограниченному листу бумаги. Это, конечно, нереально. Будем считать, что лист бумаги ограничен. Тогда ЧЕРТЕЖНИК должен уметь проверять, не находится ли он в "опасной" близости к краю листа (на самом краю он находиться не может). Опишем это действие более четко: ЧЕРТЕЖНИК может определять, находится ли край листа на расстоянии одного шага впереди него.

В развилках будем писать так:

 Если впереди край, то:

или так:

 Если впереди не край, то:

Для примера разберем следующую задачу.

Задача. ЧЕРТЕЖНИК находится у края листа, но не в углу, причем ЧЕРТЕЖНИКУ неизвестно, около какого края (левого, правого, верхнего или нижнего) и в каком из четырех возможных положений (рис. 16) он находится. Составить алгоритм, с помощью которого ЧЕРТЕЖНИК отойдет от края на один шаг.

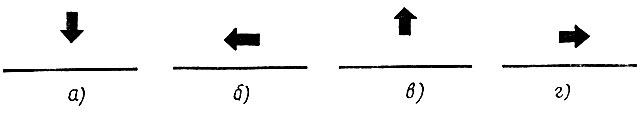
Рис. 16. Чертежник

Сразу заметим, что совершенно неважно, около какого края стоит ЧЕРТЕЖНИК: поверните лист бумаги, и левый край окажется нижним, правым или верхним. А вот положение ЧЕРТЕЖНИКА относительно края существенно. Если он находится в положении в, то ему достаточно прыгнуть; в остальных положениях ему надо сначала несколько раз повернуть налево, чтобы стать в положение в, и только затем прыгнуть. Понятно, что для каждого исходного положения написать свой (линейный) алгоритм несложно. Однако алгоритм, "обслуживающий", скажем, положение а, не годится, для остальных положений. Конечно, можно было бы попытаться составить из этих четырех алгоритмов единый алгоритм для всех случаев... Но может ли ЧЕРТЕЖНИК сразу узнать, в каком из четырех положений он находится? Увы, не всегда! Это возможно лишь в положении а - достаточно проверить условие "впереди край". Возникает идея: сначала составить алгоритм, приводящий ЧЕРТЕЖНИКА из любого исходного положения в положение а. Один из возможных алгоритмов таков: поворачиваем ЧЕРТЕЖНИКА налево, пока впереди него не окажется край листа. Ясно, что при этом надо будет сделать не более трех поворотов: из положения а - 0 поворотов, из положения б - 1 поворот, из положения в - 2 поворота, из положения г - 3 поворота. Запишем этот алгоритм, демонстрируя "движение" ЧЕРТЕЖНИКА.

 Если впереди не край, то: 
 Повернуть налево. 
 Конец ветвления.

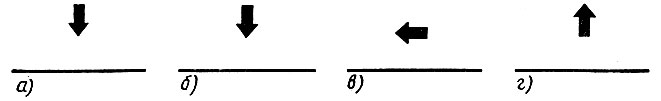
 Если впереди не край, то: 
 Повернуть налево. 
 Конец ветвления.

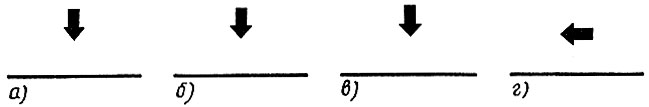
 Если впереди не край, то: 
 Повернуть налево. 
 Конец ветвления.

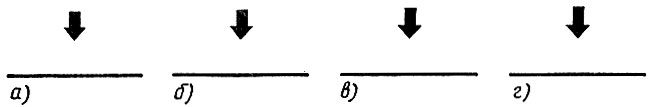
Теперь несложно завершить составление алгоритма отхода от края, дописав еще три строки:

 Повернуть налево. 
 Повернуть налево. 
 Прыгнуть.

В языке Бейсик ветвления записываются так:

 IF <условие> THEN <действие>

(ветвление в неполной форме) или так:

 IF <условно> THEN <действие> ELSE <действие>

(ветвление в полной форме). Как видите, слову "если" соответствует "IF", слову "то" - "THEN", слову "иначе" - "ELSE", а указатель конца ветвления отсутствует: дело в том, что в Бейсике запись ветвления должна размещаться в одной строке.

Вопросы

1. Какие условия умеет проверять ВЫЧИСЛИТЕЛЬ?

2. Какие условия умеет проверять ЧЕРТЕЖНИК?

Задания для самостоятельного выполнения

1. Что нарисует ЧЕРТЕЖНИК, выполнив следующий алгоритм из исходных положений, показанных на рисунке 17?

 Если впереди край, то: 
 Повернуть налево. 
 Конец ветвления. 
 Если впереди край, то: 
 Повернуть налево. 
 Сделать шаг. 
 Повернуть налево. 
 Сделать шаг. 
 Иначе: 
 Сделать шаг. 
 Повернуть налево. 
 Сделать шаг. 
 Повернуть налево. 
 Сделать шаг. 
 Повернуть налево. 
 Сделать шаг. 
 Конец ветвления.

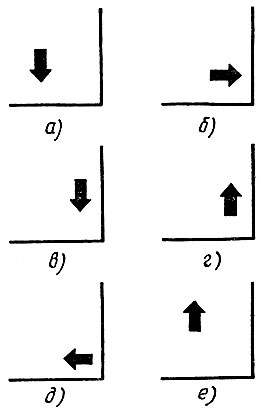
Рис. 17. Алгоритм

2. Какие значения примут переменные а и b после выполнения следующих алгоритмов? Укажите действия, которые не будут совершаться при выполнении этих алгоритмов.

а)

 Присвоить а значение 13. 
 Присвоить b значение 12. 
 Если a<b + 1, то: 
 Присвоить b значение b - а. 
 Присвоить а значение а - b. 
 Иначе: 
 Присвоить а значение а - b. 
 Присвоить b значение b - а. 
 Конец ветвления. 
 Присвоить а значение ab. 
 Если а>b2 то: 
 Присвоить b значение а - 
 Конец ветвления.

б)

 Присвоить а значение 13. 
 Присвоить b значение 12. 
 Присвоить а значение аb. 
 Если а > b2, то: 
 Присвоить b значение а - b. 
 Конец ветвления. 
 Если b > а - 1, то: 
 Присвоить b значение b - а. 
 Присвоить а значение а - b. 
 Иначе: 
 Присвоить а значение а - b. 
 Присвоить b значение b - а. 
 Конец ветвления.

3. Составить алгоритм, с помощью которого ЧЕРТЕЖНИК отойдет от края листа, если первоначально он находится в одном из следующих положений:

а) слева от ЧЕРТЕЖНИКА находится край листа, и ЧЕРТЕЖНИК не находится в углу листа;

б) ЧЕРТЕЖНИК находится в углу листа, и впереди него - край листа (где другой край - справа или слева - неизвестно);

в) ЧЕРТЕЖНИК находится в углу листа, и слева от него - край листа (где второй край - впереди или сзади - неизвестно);

г) ЧЕРТЕЖНИК находится в углу листа, и неизвестно, с какой стороны от него края листа;

д) ЧЕРТЕЖНИК находится у края листа, но неизвестно, в углу или нет.

4. В записи алгоритма вычисления значения выражения

злоумышленник одно действие поставил не на свое место. Вот как стал выглядеть алгоритм:

 Запросить х. 
 Если х6 - 4х2 + 3 = 0, то: 
 Сообщить "При таком х значение выражения не определено". 
 Иначе: 
 Присвоить у значение (х2 - 5х + 5)/(х6 - 4х2 + 3). 
 Конец ветвления. 
 Сообщить "Я нашел значение у. Вот оно:". 
 Сообщить у.

Верните действие на свое место.

5. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм нахождения модуля выражения ах² + bх + с при заданных значениях а, b, c и х.

6. Даны координаты двух точек в прямоугольной системе координат. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм, с помощью которого он сможет определить, какая из этих точек находится дальше:

а) от начала координат;

б) от окружности данного радиуса с центром в начале координат.

7. На координатной плоскости нарисованы два круга К₁ и К₂ и два прямоугольника П₁ и П₂ со сторонами, параллельными осям координат. Даны координаты центров каждого из кругов и их радиусы, а также координаты левой нижней и правой верхней вершин каждого прямоугольника. Составить для ВЫЧИСЛИТЕЛЯ алгоритмы нахождения площади пересечения:

а) кругов К₁ и К₂;

б*) прямоугольников П₁ и П₂;

в*) круга К₁ и прямоугольника П₁.

8. Составьте два алгоритма для ВЫЧИСЛИТЕЛЯ, по которым он:

а) запросит два числа и вычислит, если это возможно, сумму их десятичных логарифмов;

б) запросит два числа и вычислит, если это возможно, десятичный логарифм их произведения.

Приведите пример такой пары чисел, для которой эти алгоритмы дадут разные результаты. Для каких пар чисел результаты работы по обоим алгоритмам одинаковы?