§ 12. Метод Монте-Карло

У вас могло сложиться впечатление, что математические модели нужно строить только для решения задач, далеких от математики. На самом деле и в математике для решения задач часто требуются математические модели. Одна из таких задач - вычисление площадей. Конечно, для простейших фигур (прямоугольников, многоугольников, кругов) вычисление площади не составляет труда: надо в известные формулы подставить исходные данные. А как быть, если фигура имеет сложную форму? Итак,

Задача. Дана фигура сложной формы. Вычислить ее площадь.

Фигуры сложных форм

Можно предложить разные модели для этой задачи. Например, в шестом классе вас учили использовать палетку: на фигуру накладывается клетчатая прозрачная бумага (палетка), и подсчитывается количество квадратиков, попавших в фигуру. В этой модели молчаливо предполагается, что чем мельче клетки, тем точнее будет результат, независимо от того, каким образом наложить палетку на фигуру.

Можно придумать и "физическую" модель: скопировать фигуру на картон, аккуратно вырезать ее, взвесить и поделить на вес единичного квадрата из этого же картона.

В XI классе вы познакомитесь еще с одним способом нахождения площадей фигур: с помощью интегралов.

Однако по всем этим моделям довольно трудно составить алгоритмы для расчетов на ЭВМ.

Как видите, и для решения математических задач можно составлять различные математические модели. Математические модели жизненных задач - это "мосты" между жизнью и математикой. Математические модели, применяемые для решения математических задач,- это "мосты" между различными разделами математики. Например, метод координат позволяет создавать алгебраические модели геометрических объектов.

Математическая модель, которую мы сейчас построим, может показаться вам неожиданной, но она позволяет очень эффективно применять ЭВМ для решения задач на нахождение площадей, объемов и т. п.

Поместим данную фигуру в квадрат. Будем наугад (как говорят математики, случайным образом) бросать точки в этот квадрат. Естественно предполагать, что чем больше площадь фигуры, тем чаще в нее будут попадать точки. Представьте себе квадратный дворик и в нем детскую площадку. Каждому ясно, что во время снегопада количество снежинок, попавших на детскую площадку, пропорционально ее площади. Таким образом, можно сделать допущение: при большом числе точек, наугад выбранных внутри квадрата, доля точек, содержащихся в данной фигуре, приближенно равна отношению площади этой фигуры к площади квадрата.

Такой метод приближенного нахождения площадей фигур носит название метода Монте-Карло (по названию города, где расположена знаменитая рулетка, которую можно рассматривать как "генератор" случайных чисел).

Только случайность поможет вам найти площадь фигуры методом Монте-Карло

Несложно определить, что в нашей модели - исходные данные, а что - результат. Обозначим данную фигуру буквой F.

Исходными являются сторона а квадрата, содержащего фигуру F, и количество точек N, которые мы будем случайным образом выбирать внутри квадрата. Результатом является площадь S фигуры F. Если через М обозначить число тех наугад выбранных точек, которые содержатся в фигуре F, то площадь S приближенно равна a² M/N. Разумеется, к связям между исходными данными и результатом следует отнести и математические соотношения, позволяющие определить, попала ли выбранная точка в фигуру F.

Эти соотношения будут отличать модели, построенные для разных фигур. Значит, фактически мы описали не одну модель, а скорее - некоторый способ получения моделей. Для каждой конкретной фигуры будет получаться своя модель.

Давайте рассмотрим математическую модель для приближенного нахождения площади круга радиуса R. Формула площади круга вам, конечно, известна: S = πR². Однако, если вы помните, эту формулу вам сообщили фактически без доказательства. Вот подходящий случай проверить ее с помощью ЭВМ!

Пусть, для определенности, R=1. На рисунке 21 изображен круг радиуса 1, заключенный в квадрат со стороной а=2. Таким образом, в качестве фигуры F выступает круг единичного радиуса. Выбрать точку - это значит задать ее координаты: числа х и у. Точка принадлежит квадрату, если -1 ≤ x ≤ 1 и - 1 ≤ у ≤ 1. Если x²+y² ≤ 1, то точка попадает в круг F, иначе она вне круга. Это и есть математическое соотношение, позволяющее для каждой точки определять, лежит ли она в F.

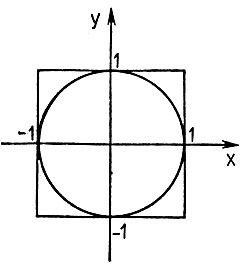
Рис. 21. Круг радиуса 1

Математическая модель вычисления площади круга построена и, казалось бы, можно приступать к составлению алгоритма для ВЫЧИСЛИТЕЛЯ. Однако, составляя алгоритм мы быстро обнаружим, что запас допустимых действий ВЫЧИСЛИТЕЛЯ недостаточен: он не умеет выбирать числа случайным образом. Ну что ж, пополним запас допустимых действий ВЫЧИСЛИТЕЛЯ: по команде:

 Присвоить z значение RND (а)

ВЫЧИСЛИТЕЛЬ присваивает переменной г случайное значение, заключенное между - а и а. Запишем алгоритм:

 Запросить количество точек N. 
 Присвоить номеру I выбранной точки значение 0. 
 Присвоить количеству точек М, попавших в фигуру, значение 0. 
 Пока I≤N, повторять: 
 Присвоить абсциссе X значение RND (1). 
 Присвоить ординате Y значение RND (1). 
 Если Х2 + Y2 ≤ 1, то: 
 Присвоить М значение М + 1. 
 Конец ветвления. 
 Присвоить I значение I + 1. 
 Присвоить S значение 4M/I. 
 Сообщить "Число выбранных точек; площадь:" 
 Сообщить I, S. 
 Конец цикла.

Вычислительный эксперимент с этим алгоритмом вы проведете, выполняя лабораторную работу 5.

В языке Бейсик выбор случайного числа между - а и а осуществляется по команде

 LET z = 2 ∗ a ∗ RND(l) - a

Вопрос

1. Какое допустимое действие ВЫЧИСЛИТЕЛЯ позволяет ему выбирать случайные числа?

Задания для самостоятельного выполнения

1°. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм нахождения площадей следующих фигур методом Монте-Карло:

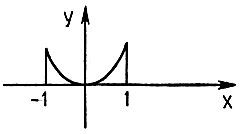
Рис. 22. Кривая задана уравнением у=х²

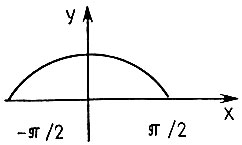
Рис. 23. Кривая задана уравнением y = cos x

Рис. 24. Алгоритм нахождение площадей

2. Школьник решил обучить ВЫЧИСЛИТЕЛЯ играть с ним в игру "Угадай-ка" и составил соответствующий алгоритм. Будучи ярым противником компьютерных игр, злоумышленник стер в алгоритме школьника одну строку. Вот что получилось:

 Запросить а. 
 Присвоить z значение RND (а) + а. 
 Присвоить N значение 0. 
 Пока |b - z|>1, повторять: 
 Сообщить "Попробуйте угадать задуманное число". 
 Сообщить "Введите свое число". 
 Запросить b. 
 Если b - z>1, то: 
 Сообщить "Задуманное число меньше". 
 Конец ветвления. 
 Если b - z< - 1, то: 
 Сообщить "Задуманное число больше". 
 Конец ветвления. 
 Присвоить N значение N + 1. 
 Конец цикла. 
 Сообщить "Вы угадали!". 
 Сообщить "Число попыток:". 
 Сообщить N.

Восстановите стертую строку. Какой диалог ведет ВЫЧИСЛИТЕЛЬ, выполняя исправленный вами алгоритм?

3°. (Задача с детективным сюжетом.) Каждый день резидент приходит на встречу со своим агентом в случайный момент времени с 11 до 13 часов и ждет его 15 минут. В свою очередь, агент приходит на встречу с резидентом каждый день также в случайный момент времени от И до 13 часов и тоже ждет 15 минут. Как часто в течение года встречаются резидент и агент? Составьте математическую модель и алгоритм решения задачи.

Детективный сюжет

4°. Ученик пишет квадратные уравнения вида x² + px + q = 0 выбирая коэффициенты р и q случайным образом из отрезка [-1; 1]. С какой частотой он будет писать уравнения, имеющие действительные корни? Составьте математическую модель и алгоритм решения этой задачи.

5°. Завод, стоящий на берегу реки, сбрасывает в нее ежедневно случайным образом (из-за неисправности очистных сооружений) от 0 до 30 кг вредных веществ. За каждый килограмм сверх 15 завод обязан заплатить штраф 100 р. Прибыль завода от реализации его продукции - 700 р. в день. Как часто в течение пятилетки штраф превзойдет прибыль? Рентабелен ли такой завод? Составьте математическую модель и алгоритм решения гой задачи.

6°. а) Постройте математическую модель игры в "Спортлото". Составьте алгоритм для ВЫЧИСЛИТЕЛЯ, помогающий вам играть в эту лотерею.

б) (К решению этой задачи дети до 16 лет не допускаются.) Постройте математическую модель игры в рулетку. Составьте алгоритм, имитирующий эту игру с помощью ВЫЧИСЛИТЕЛЯ.

7. Учитель хочет, чтобы ВЫЧИСЛИТЕЛЬ помог ему проверить знание учащимися таблицы умножения, задавая сомножители случайным образом. Составьте математическую модель и алгоритм опроса учащихся. (Указание: воспользуйтесь решением задачи 15,б к параграфу 11.)