§ 17. Табличный способ организации данных

В этом параграфе мы расскажем об одном из самых распространенных способов организации данных - табличном. Без преувеличения можно сказать, что с таблицами вы сталкиваетесь ежедневно. Таблица итогов шахматного турнира и классный журнал, таблица умножения на обложке вашей тетради и план кинозала - все это примеры табличной организации данных.

Допустим, что 26 апреля прошлого года 10 "а" класс писал сочинение по литературе, и нам нужно узнать, какую оценку получил ученик этого класса Иванов И. Берем классный журнал !"а" класса за прошлый год, открываем его на странице "Литература", находим строку с оценками Иванова И., столбец за 26 апреля. На их пересечении и записана искомая оценка.

После уроков вы пришли в кинотеатр. Как занять место в зале согласно купленному билету? Сначала, двигаясь по проходу, ищем свой ряд, а затем идем вдоль него до нужного места.

Нетрудно заметить сходство этих примеров. Хотя школьные оценки на странице классного журнала и места в зрительном зале имеют мало общего, расположены они в принципе одинаково: в несколько рядов (строк) одинаковой длины. Такой способ расположения данных и называется табличным. Может случиться и так, что в таблице всего одна строка. Такую таблицу называют линейной. Таблицу, состоящую из нескольких строк, называют прямоугольной.

В таблице каждый элемент - на своем месте

Чтобы можно было оперировать с элементами линейных и прямоугольных таблиц, надо каким-то образом обозначать таблицы и их элементы. Обычно для обозначения таблиц используют латинские буквы. Договоримся нумеровать строки таблиц сверху вниз, а столбцы - слева направо. Элемент, расположенный линейной таблицы А, обозначают A(i), а элемент, расположенный на пересечении i-й строки и j-го столбца прямоугольной таблицы X, обозначают X(i, j). Например, в таблице А

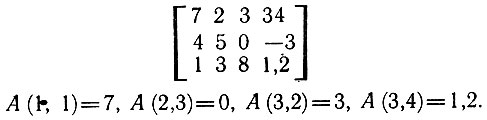
Вопросы

1. Что такое табличная форма организации данных?

2. Какие таблицы называются

а) линейными;

б) прямоугольными?

3. Как обозначаются таблицы и их элементы?

Задания для самостоятельного выполнения

1. Определить, как выглядит таблица А, состоящая из 4 строк и 5 столбцов, если для любых i и j

а) A (i, j) = ij;

б) A (i, j) = i;

в) A (i, j) = 1;

г) A (i, j) = max {i, j};

д) A (i, j) = min {i, j};

е) А (i, j)= {i - j};

ж) А (i, j) равняется 1, если i≤j, и 0, если i>j.

2. Дана таблица В. Запишите, как выражаются ее элементы В (i, j) через i и j, если таблица имеет вид:

а)

(в этой таблице 4 строки и п столбцов);

б)

(в этой таблице п строк и п столбцов);

в) |n n-1 ... 2 1| (в этой линейной таблице n столбцов).

3. Приведите пример таблицы Л, состоящей из п строк и пг столбцов, в которой элементы А (i, j) и А (i, j + 1) равны для любых i≤n и j≤m - 1.

4. В следующей таблице приведены итоги шахматного турнира:

Сколько очков набрал победитель турнира?