§ 18. Таблицы и исполнители

Хорошо знакомый вам исполнитель ЧЕРТЕЖНИК в своей работе совсем не пользуется таблицами. Поэтому мы продемонстрируем табличный способ организации данных на примере нового для вас исполнителя. Назовем его РОБОТ-МАНИПУЛЯТОР, или просто РОБОТ. На складе, где он работает, имеется большой прямоугольный стеллаж, в ячейках которого находятся ящики с однотипными деталями (микросхемами, транзисторами и т. д.). РОБОТ может перемещаться вдоль стеллажа, не выходя при этом за его пределы. Работа у него несложная: по запросу оператора он ищет нужные детали и, поместив их в свой грузовой отсек, доставляет на рабочее место.

Укажем список допустимых действий РОБОТА-МАНИПУЛЯТОРА.

1. Запросить наименование детали.

2. Переместиться к левой нижней ячейке стеллажа.

3. Переместиться к началу ряда.

4. Переместиться к соседней сверху (снизу, справа, слева) ячейке.

5. а) Переложить деталь из ячейки в грузовой отсек, б) Переложить деталь из грузового отсека в ячейку. (Ячейка, о которой идет речь в пунктах а) и б),- та, напротив которой находится РОБОТ.)

6. Проверить одно из следующих условий:

а) можно шагнуть вверх (вниз, вправо, влево) или нельзя;

б) есть деталь в ячейке, напротив которой находится РОБОТ, или нет;

в) совпадает наименование детали в ячейке, напротив которой находится РОБОТ, с наименованием запрошенной детали или не совпадает;

г) пуст грузовой отсек или не пуст.

Теперь мы можем приступить к составлению алгоритмов для нашего РОБОТА-МАНИПУЛЯТОРА. Научим его находить на стеллаже все детали заданного вида. Ясно, что робот должен просматривать все ячейки стеллажа в поисках нужных деталей. Как же проще всего организовать просмотр ячеек? Например, так: сначала РОБОТ перемещается к первой слева ячейке нижнего ряда стеллажа, а затем просматривает ряды стеллажа один за другим, пока не дойдет до верхнего ряда; каждый ряд он рассматривает, двигаясь вдоль него слева направо, а после просмотра он возвращается к крайней слева ячейке соответствующего ряда.

Давайте начнем с написания вспомогательного алгоритма "Просмотр ряда". Выполняя этот алгоритм, РОБОТ перемещается вдоль ряда слева направо, проверяя, совпадают ли наименования встречаемых по дороге деталей с наименованием запрошенной детали. В случае совпадения он перекладывает деталь из ячейки в грузовой отсек.

 Алгоритм "Просмотр ряда". 
 Пока можно идти вправо, повторять: 
 Если наименование детали, лежащей в ячейке, совпадает с 
 наименованием запрошенной детали, то: 
 Переложить деталь из ячейки в грузовой отсек. 
 Конец ветвления. 
 Шаг вправо. 
 Конец цикла. 
 Если наименование детали, лежащей в ячейке, совпадает с 
 наименованием запрошенной детали, то: 
 Переложить деталь из ячейки в грузовой отсек. 
 Конец ветвления.

Как же теперь составить основной алгоритм? По-видимому, здесь необходимо применить циклический способ организации действий. РОБОТ должен переместиться к первой слева ячейке нижнего ряда стеллажа, просмотреть первый ряд, вернуться к его началу, подняться на одну ячейку вверх, просмотреть второй ряд, вернуться к его началу, подняться на одну ячейку вверх и так далее. Значит, в цикле должны повторяться действия:

 Выполнить алгоритм "Просмотр ряда". 
 Переместиться к первой слева ячейке ряда. 
 Сделать шаг вверх.

РОБОТ должен повторять эти три действия до тех пор, пока не дойдет до верхнего ряда стеллажа. Вот как выглядит искомый алгоритм:

 Запросить наименование детали. 
 Переместиться к первой слева ячейке нижнего ряда. 
 Пока можно идти вверх, повторять: 
 Выполнить алгоритм "Просмотр ряда". 
 Переместиться к первой слева ячейке ряда. 
 Шаг вверх. 
 Конец цикла. 
 Выполнить алгоритм "Просмотр ряда".

Табличная форма организации данных полезна и при решении вычислительных задач, которые, как вы уже знаете, возникают повсюду. Поговорим, к примеру, о погоде. Допустим, не доверяя Гидрометцентру, вы решили сами заняться изучением погоды. Для этого вам, конечно, потребуется информация о ежемесячном количестве осадков, выпавших в вашем районе. За несколько лет наберется так много данных, что их надо как-то упорядочить. Лучше всего занести данные в таблицу. Каждая строка этой таблицы содержит 12 чисел: результаты измерений за один год. Число строк равно количеству лет, когда производились измерения. Располагая этой таблицей, можно решать разнообразные задачи: находить среднегодовое количество осадков, самый "влажный" месяц в году или за несколько лет и так далее. Можно попытаться даже прогнозировать погоду.

Не храните данные бессмысленной грудой - записывайте их в таблицы!

Прежде чем составлять алгоритмы решения этих задач, надо позаботиться, чтобы исполнитель мог работать с числовыми таблицами. Для этого мы не будем выбирать нового исполнителя, а снова расширим запас допустимых действий ВЫЧИСЛИТЕЛЯ. Прежде всего, ВЫЧИСЛИТЕЛЮ нужно уметь запрашивать и сообщать таблицу. Поэтому будем считать допустимыми действия "Запросить таблицу" и "Сообщить таблицу". После слова "таблицу" надо указать обозначение таблицы, а также (например, в скобках) число строк и столбцов в ней:

 Запросить прямоугольную таблицу А из 21 строки и 12 столбцов. 
 Запросить линейную таблицу В из 52 элементов. 
 Сообщить линейную таблицу С (11). 
 Сообщить таблицу D (17,5).

Будем считать также, что в команде присваивания, кроме обычных переменных, могут использоваться переменные, являющиеся элементами таблиц. При этом ВЫЧИСЛИТЕЛЬ использует обычные обозначения для этих элементов (см. § 17). Номера строк и столбцов могут быть как числами, так и алгебраическими выражениями: А (1,2), В (I + J), С(I + 1, 2·J). Вот примеры команд присваивания:

 Присвоить A (2,1) значение A (I, J)⋅ B (К)2. 
 Присвоить X значение С(2)⋅sin (В (К) + Х).

Для демонстрации работы ВЫЧИСЛИТЕЛЯ с таблицами посмотрим, какой вид примет следующая таблица A

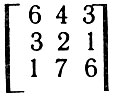
после выполнения им, например, такой последовательности действий:

 Запросить таблицу А (3, 3). 
 Присвоить A (1, 1) значение 2. 
 Присвоить A (2, 1) значение A (2, 3). 
 Присвоить A (3, 2) значение A (1, 1) + A (1, 2). 
 Присвоить ω значение A (1, 1) + A (1, 2) A (1, 3). 
 Сообщить таблицу A (3, 3).

Чтобы проследить за выполнением этого алгоритма, надо прежде всего вспомнить, как выполняется действие присваивания: вычисляется значение выражения, стоящего в правой части, а затем этому значению дается имя переменной, стоящей в левой части. При этом старое значение переменной забывается. Например, в четвертом действии нашего алгоритма А (1,1) обозначает уже не число 6, как в начале, а число 2.

При выполнении этого алгоритма таблица А будет меняться следующим образом:

Переменная ω примет значение 14.

Допустим теперь, что у нас имеется линейная таблица из двенадцати элементов, в которую занесены результаты ежемесячных измерений количества осадков, выпавших в 1987 г. Составим для ВЫЧИСЛИТЕЛЯ алгоритм, с помощью которого он определит число засушливых месяцев, когда количество осадков было ниже, скажем, 10 мм.

Обозначим таблицу наблюдений буквой А, а искомое число месяцев - буквой n. ВЫЧИСЛИТЕЛЬ должен просматривать элементы таблицы А с первого по двенадцатый и каждый раз, встретив число, меньшее 10, добавлять к значению n единицу (сначала n равняется 0). Не правда ли, очень похоже на поиск нужных деталей на стеллаже? Роль "грузового отсека" играет переменная n. Если бы ВЫЧИСЛИТЕЛЬ мог определять, рассматривает он крайнюю клетку таблицы или нет, мы могли бы почти дословно переписать алгоритм "Просмотр ряда". Как же ВЫЧИСЛИТЕЛЬ "узнает", что таблица закончилась? Для этого он должен "помнить" номер рассматриваемого элемента таблицы и сравнивать его с числом 12. Обозначим этот номер буквой i.

Запишем алгоритм решения нашей "метеорологической" задачи:

 Присвоить переменной n (число засушливых месяцев) начальное значение 0. 
 Присвоить i (номеру месяца) значение 1. 
 Пока i≤12, повторять: 
 Если A (i) < 10, то: 
 Присвоить п значение n + 1. 
 Конец ветвления. 
 Присвоить i значение i + 1. 
 Конец цикла. Сообщить n.

Как видите, переменная i выступает в роли "счетчика", подсчитывающего, сколько раз выполняется набор действий, входящих в тело цикла. Подобные циклы со "счетчиком" часто применяются при работе с таблицами. Будем использовать для них специальную форму записи:

 Для каждого i от L до R: 
 P1 
 Р2 
 ... 
 Рn 
 Конец цикла по i.

Здесь i - "счетчик", L - нижняя, a R - верхняя границы изменения i; P₁, Р₂, ..., Р_n - действия, которые выполняются в цикле. Разумеется, можно использовать другие обозначения для "счетчика" и границ цикла. Кроме того, вместо L и R можно писать алгебраические выражения или просто числа.

Выполняя этот цикл (назовем его циклом "Для каждого"), ВЫЧИСЛИТЕЛЬ сначала присвоит i значение L. Затем он проверит, больше ли i, чем R; если да, то цикл заканчивается (не начавшись), если нет, то ВЫЧИСЛИТЕЛЬ выполнит действия P₁, P₂ и т. д., число i увеличится на 1, и для этого нового значения i повторяется тело цикла до тех пор, пока i не превзойдет R.

Приведем блок-схему цикла "Для каждого" (рис. 38):

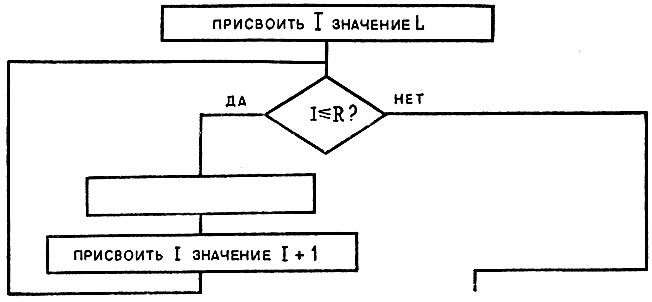
Рис. 38. Блок-схема 'Для каждого'

Запишем алгоритм нахождения числа засушливых месяцев в году, используя цикл в форме "Для каждого":

 Присвоить переменной n (число засушливых месяцев) начальное значение 0. 
 Для каждого i от 1 до 12: 
 Если А (i) < 10, то: 
 Присвоить п значение n + 1. 
 Конец ветвления. 
 Конец цикла по i. 
 Сообщить n.

Допустим теперь, что нам известна таблица наблюдений за несколько лет и нужно подсчитать количество п засушливых месяцев за этот период. В таблице наблюдений (обозначим ее буквой В) число строк равно числу лет, а в каждой строке по 12 элементов. Естественно оформить в качестве вспомогательного алгоритма подсчет числа засушливых месяцев за год. Аргументами в нем являются номер года (строки в таблице наблюдений) р и число х засушливых месяцев за предыдущие годы рассматриваемого периода. Результатом является новое значение переменной n.

 Алгоритм "Один год". 
 Аргументы: номер года р и число х засушливых месяцев за предыдущие годы. 
 Результат: n (число засушливых месяцев за р лет). 
 Присвоить n начальное значение, равное х. 
 Для каждого q от 1 до 12: 
 Если В(р, q)< 10, то: 
 Присвоить п значение n + 1. 
 Конец ветвления. 
 Конец цикла по q.

Основной алгоритм теперь запишется так:

 Сообщить "Введите число лет". 
 Запросить k. 
 Сообщить "Введите таблицу наблюдений". 
 Запросить таблицу В (k, 12). 
 Присвоить переменной п (число засушливых месяцев) начальное значение 0. Для каждого i от 1 до m: 
 Выполнить алгоритм "Один год" при х = n, p = i. 
 Конец цикла по i. 
 Сообщить "Число засушливых месяцев". 
 Сообщить n.

Вопросы

1. Какими допустимыми действиями обладает РОБОТ-МАНИПУЛЯТОР?

2. Какие допустимые действия позволяют ВЫЧИСЛИТЕЛЮ оперировать с таблицами?

3. Как оформляется цикл "Для каждого"? Как он изображается при помощи блок-схемы?

Задания для самостоятельного выполнения

1. Составьте для РОБОТА-МАНИПУЛЯТОРА алгоритмы, выполнив которые он:

а) отойдет от края стеллажа;

б) положит в грузовой отсек деталь из крайней правой ячейки верхнего ряда стеллажа;

в) соберет все диоды из первого справа столбца стеллажа;

г) соберет все резисторы из третьего сверху ряда стеллажа;

д) оставит в нижнем ряду стеллажа только детали выбранного типа;

е) оставит на стеллаже только детали выбранного типа;

ж) расположит детали из нижнего ряда стеллажа подряд (без пропусков), начиная с левой ячейки ряда;

з) расположит все детали, находящиеся на стеллаже, подряд, начиная с левой нижней ячейки стеллажа;

и*) положит все резисторы, имеющиеся на стеллаже, подряд, начиная с левой нижней ячейки стеллажа;

к*) определит, каких деталей на стеллаже меньше - диодов или резисторов, положив "дефицитную" деталь в левую нижнюю ячейку стеллажа (или оставив эту ячейку пустой, если "дефицитная" деталь на стеллаже отсутствует);

л*) рассортирует детали на стеллаже, положив сначала подряд все диоды, затем - все резисторы и т. д.

2. Дана таблица А:

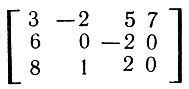
Как изменится таблица А после выполнения следующих алгоритмов?

а)

 Присвоить А (1, 1) значение 2. 
 Присвоить А (3, 2) значение A (1, 1) + A (3, 2). 
 Если А (3, 2)>3, то: 
 Присвоить А (3, 4) значение 2А (3, 1). 
 Иначе: 
 Присвоить A (1, 4) значение A (3, 2) + 3. 
 Конец ветвления. 
 Для каждого I от 1 до 3: 
 Присвоить A (I, I значение I2. 
 Конец цикла по I.

б)

 Присвоить A (2, 2) значение 2. 
 Присвоить A (1, 2) значение A (2, 2) - A (1, 2). 
 Если A (1,2)>3, то: 
 Присвоить A (3, 3) значение A (3, 1) / A (1, 1). 
 Иначе: 
 Присвоить A (1, 4) значение 3A (3, 2). 
 Конец ветвления. 
 Для каждого I от 1 до 3: 
 Присвоить A (I, 4 - 1) значение A (4 - I, I). 
 Конец цикла по I.

3°. В алгоритме вычисления суммы кубов элементов таблицы A, имеющей 4 строки и 3 столбца, злоумышленник поменял местами две строки. Вот что у него получилось:

 Присвоить S значение 0. 
 Для каждого I от 1 до 4: 
 Для каждого J от 1 до 3: 
 Присвоить S значение S + A(I, J)3. 
 Конец цикла по I. 
 Конец цикла по J.

Какие строки поменял местами злоумышленник?

4. Чему будет равно значение М после выполнения следующего алгоритма? Сколько раз будет исполняться тело цикла?

 Присвоить М значение 0. 
 Для каждого I от 1 до 8: 
 Присвоить М значение M + I. 
 Присвоить I значение I + 1. 
 Конец цикла по I.

5°. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм проверки того, что в данной квадратной таблице равны элементы, расположенные симметрично относительно диагонали, проведенной из левого верхнего угла в правый нижний угол:

6°. Составьте для ВЫЧИСЛИТЕЛЯ алгоритмы, выполнив которые он заполнит и сообщит таблицы из задач 2,а - 2,в (§ 17).

7°. Дана прямоугольная таблица. Составьте алгоритмы, по которым ВЫЧИСЛИТЕЛЬ:

а) заменит в таблице все отрицательные элементы кулями, а положительные оставит неизменными;

б) поменяет в таблице первые две строки местами;

в) поменяет в таблице первые два столбца местами.

8°. Пусть дана таблица наблюдений В (см. текст § 18). Составьте алгоритм для определения:

а) самого засушливого месяца за один год;

б) самого влажного месяца за один год;

в) общего количества осадков, выпавших за один год;

г) среднего количества осадков за месяц в течение одного года;

д) числа месяцев в течение одного года, когда количество осадков превышало 40 мм.

9°. Используя алгоритмы решения задачи 8 в качестве вспомогательных, составьте алгоритмы определения:

а) самого засушливого и самого влажного месяца за все время наблюдений;

б) общего количества осадков, выпавших за время наблюдений;

в) наиболее засушливого (влажного) года.

10. Дана таблица результатов шахматного турнира. Составьте для ВЫЧИСЛИТЕЛЯ алгоритм определения победителя этого турнира.

11. Составьте математическую модель и алгоритм решения следующей задачи.

3адача. На заводе имеется несколько цехов. В памяти ВЫЧИСЛИТЕЛЯ постоянно имеются сведения о наличии сырья в каждом из них. Требуется определить номер цеха, в котором осталось меньше всего сырья.