§ 23. Подпрограммы и определяемые функции

Давайте теперь поговорим об оформлении и вызове подпрограмм.

Как вы помните, вспомогательные алгоритмы начинались с заголовка. Вот пример заголовка:

 Алгоритм "Название". 
 Аргументы х, у. 
 Результаты с, d.

В Бейсике заголовки и комментарии писать необязательно, однако если вы хотите облегчить себе и другим понимание алгоритма (некоторые программисты преследуют, по-видимому, противоположные цели), то пишите комментарии, используя слово REM (REMARK - пояснение). Например, приведенный только что заголовок перепишется так:

В конце подпрограммы надо обязательно ставить команду RETURN (возвратиться).

Нумеруя строки программы, надо располагать подпрограммы после текста основной программы (вам уже знакомо это правило).

Как вы видели, наша подпрограмма "Название" располагается, начиная со строки 1000. Вспомните: чтобы исполнитель выполнил этот алгоритм при определенных значениях x и у, скажем, при х = а, у = b, использовалась команда вызова:

На языке Бейсик этой команде соответствует последовательность из нескольких команд: сначала нужно присвоить переменным х к у значения а и b, а затем записать команду GOSUB 1000 (выполнить подпрограмму, начинающуюся со строки 1000). Проиллюстрируем сказанное на примере задачи на нахождение максимума из трех чисел. В § 14 мы составили алгоритм решения этой задачи с использованием вспомогательного алгоритма "Поиск максимума из двух чисел":

 Алгоритм "Поиск максимума из двух чисел". 
 Аргументы х, у. 
 Результат т. 
 Если х>у, то: 
 Присвоить m значение х. 
 Иначе: 
 Присвоить m значение у. 
 Конец ветвления.

Основной алгоритм мы записывали так:

 Запросить а, b, с. 
 Выполнить алгоритм "Поиск максимума из двух чисел" при 
 x = а, у = b. 
 Выполнить алгоритм "Поиск максимума из двух чисел" при 
 х = m, у = с. 
 Сообщить m.

Приведем перевод этого алгоритма на Бейсик.

 10 INPUT А,В, С 
 20 X = A : Y = B 
 30 COSUB 80 
 40 X = M : Y = C 
 50 GOBUB 80 
 60 PRINT M 
 70 STOP 
 80 REM Поиск максимума из двух чисел. Аргументы x, у; результат М 
 90 IF X>Y THEN М = X ELSE M = Y 
 100 RETURN

В языке Бейсик можно использовать и другой вид подпрограмм - так называемые подпрограммы-функции.

Вы уже знаете, что при записи выражений на языке Бейсик можно употреблять обычные функции (синус, косинус и т. д.). Зачастую, однако, этих функций бывает недостаточно. Допустим, что в нашей программе часто встречается вычисление значения функции

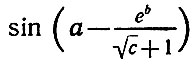
при разных значениях аргументов а, b и с. Конечно, можно написать подпрограмму вычисления значений этой функции и каждый раз к ней обращаться. Но гораздо удобнее как-то обозначить функцию, а затем использовать ее обозначение в записи выражений так же, как используются SIN, COS и т. д. Для этого и служат подпрограммы-функции. В отличие от обычных подпрограмм, каждая из них содержит только одну команду. Эта команда определяет имя новой функции и задает правило вычисления ее значений. Имя функции должно состоять из трех или четырех латинских букв, первые две из которых FN (сокращение от английского слова FUNCTION - функция), а остальные - любые латинские буквы, например FNG или FNST. Команда выглядит так:

DEF FNG (X) = U.

Здесь U - выражение, X - один или несколько аргументов, а DEF - сокращение английского слова define (определить). Для нашей функции эта команда запишется так:

DEF FNY (А, В, C) = SIN (A-EXP (B)/(SQR (C) + l))

(вы уже поняли, что функцию мы назвали FNY).

Покажем, как использовать подпрограммы-функции на примере следующей задачи

Задача. Даны три стороны треугольника. Определить его углы.

Из теоремы косинусов легко выводится формула: угол между сторонами а и b равен

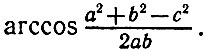
К сожалению, из всех обратных тригонометрических функций в Бейсике есть только арктангенс (ATN). Поэтому нам придется определить в программе две функции: арккосинус (через арктангенс) и функцию для вычисления углов (с использованием арккосинуса). В справочнике мы нашли следующую формулу, связывающую арккосинус с арктангенсом:

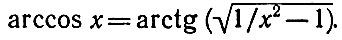
Теперь у нас есть все необходимое для составления программы. Вот она:

 10 DEF FNAC (X) = ATN (SQR (1/Х^2-1)) 
 20 DEF FNUG (A, B, C) = FNAC ((А^2 + В^2 - С^2)/(2∗А∗В)) 
 30 INPUT "ВВЕДИТЕ ДЛИНЫ СТОРОН ТРЕУГОЛЬНИКА" А, В, С 
 40 PRINT "УГОЛ A = "FNUG (В, С, А) "РАДИАН" 
 50 PRINT "УГОЛ B = "FNUG (А, С, В) "РАДИАН" 
 60 PRINT "УГОЛ C = "FNUG (А, В, С) "РАДИАН"

И наконец - подготовка к лабораторной работе. На этот раз мы азберем задачу из биологии.

Задача. Для производства вакцины на заводе планируется выращивать культуру бактерий. Известно, что если масса бактерий - х г, то через день она увеличится на (а - bх) х г, где коэффициенты а и b зависят от вида бактерий. Завод ежедневно будет забирать для нужд производства т г бактерий. Для составления плана важно знать ответ на вопрос: как изменяется масса бактерий через 1, 2, 3, ..., 365 дней (до конца года)? Ответьте на этот вопрос.

Вакцина

По сути дела, все упрощающие предположения высказаны в условии задачи. Там же фактически перечислены исходные данные: коэффициенты а и b, масса бактерий, забираемых для нужд производства т, начальная масса бактерий х₀. Результатами являются значения массы бактерий через 1, 2, 3, 4, 5 ... дней. Мы будем обозначать эти значения x₁, x₂, ... Указать общую формулу для определения x_t через t сложно. Да она и не нужна. Ведь если известно значение х_t то легко определить x_t+1

т. е.

В частности, через сутки масса бактерий будет равна

Затем по х₁ вычисляется x₂, по x₂ вычисляется x₃ и т. д. Правда, очередное значение х может стать нулем или даже отрицательным числом. Что же делать в таком случае? Надо, конечно, сигнализировать о ЧП, "останавливать производство" и тщательно анализировать причины создавшейся ситуации.

Эти соотношения и определяют связь между исходными данными и результатами.

Как видите, хотя в этой задаче нам и не удалось записать общую формулу членов последовательности, мы тем не менее можем вычислить любой ее член, зная предыдущие. Такой способ задания последовательностей называется рекуррентным. На вид несколько необычный, он часто оказывается более простым, чем вычисление по формуле общего члена последовательности.

Математическая модель построена. Составим алгоритм методом пошаговой детализации. Первоначальная блок-схема выглядит так, как показано на рисунке 41. В этой блок-схеме в детализации нуждается только блок "Вычислить следующее значение x...". Оформим его в виде вспомогательного алгоритма.

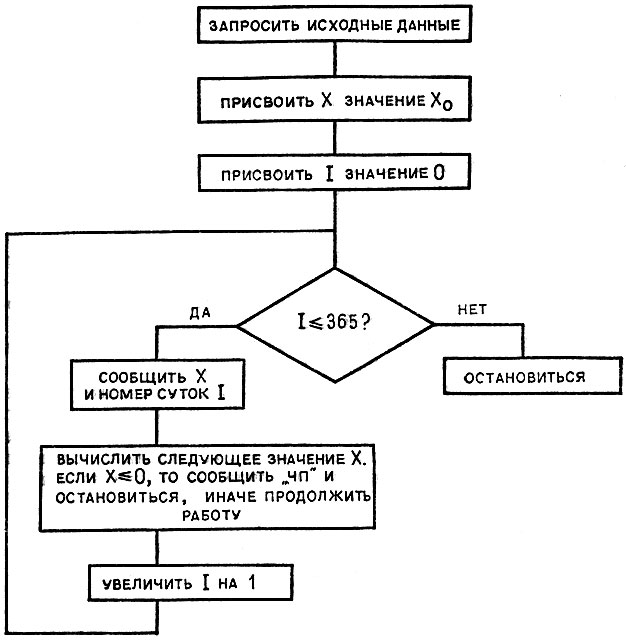
Рис. 41. Блок-схема детализации

 Алгоритм "Вычисление следующего значения массы". 
 Аргументы у, а, b, m. 
 Результат х. 
 x = у + (а - bу) у - m. 
 Если х≤0, то: 
 Сообщить "ЧП. Бактерии погибли!". 
 Стоп. 
 Конец ветвления.

Теперь запишем основной алгоритм (начальную массу бактерий мы обозначили через р):

 Сообщить "Введите коэффициенты a, b и массу m". 
 Запросить а, b, m. 
 Сообщить "Введите начальное значение массы бактерий". 
 Запросить начальное значение массы бактерий р. 
 Присвоить х значение р. 
 Для каждого i от 0 до 365: 
 Сообщить "Значения х, i". 
 Сообщить x, i 
 Выполнить алгоритм "Вычисление следующего значения массы" при у = х и имеющихся значениях а, b, m. 
 Конец цикла по i.

Перевод на Бейсик, как обычно, предоставляем вам.

Вопросы

1. Как оформляются подпрограммы в языке Бейсик?

2. Как оформляется вызов подпрограмм в языке Бейсик?

3. Для чего служат и как записываются подпрограммы-функции?

Задания для самостоятельного выполнения

1. Переведите на язык Бейсик алгоритмы решения задач 7, 8 к § 14, задач 4-6 к § 15 и задач 5-7 к § 16.

2. Найдите и исправьте ошибки в следующих программах. а) Программа вычисления максимума из значений двух выражений sin (x^x)+COS (x^х) и sin x+cos х:

 10 REM Поиск максимума ив двух чисел. 
    Аргументы х,у результат М 
 20 IF X>Y THEN М=Х ELSE M=Y 
 30 RETURN 
 40 INPUT X 
 50 GOSUB 10 : X = SIN(X^X) + C0S(X^X) : Y = SIN(X) + COS(X) 
 60 PRINT "МАКСИМАЛЬНОЕ ЗНАЧЕНИЕ "М

б) Программа нахождения значений функций sin (cos (2^х - 2^-x)) и tg(cos2 (2^x - 2^-х)) на отрезке [0; 1] с шагом 0,1:

 10 FOR I = 0 ТО 10 
 20 Х = I/10 
 30 PRINT SIN(FNY(X)),TAN(FNY(X)^2) 
 40 NEXT I 
 50 DEF FNY(X) = C0S(2^X-2^(-X)) 
 60 RETURN

3. Для упорядочивания трех чисел а, b, с по возрастанию была написана программа. Злоумышленник стер в ней строку под номером 20. Восстановите стертую строку.

10 INPUT А,В,С 
20...........
30 G0SUB 100
40 IF C<=L THEN PRINT C,L,RiST0P
50 IF C>=R THEN PRINT L,R,C ELSE PRINT L,C,R
60 END     
100 REM ПОДПРОГРАММА УПОРЯДОЧЕНИЯ ДВУХ ЧИСЕЛ.
    АРУМЕНТЫ X,Y.  РЕЗУЛЬТАТЫ L,R  (L<R). 
110 IF X<Y THEN L = X : R = Y ELSE L = Y : R = X 
120 RETURN

4. Напишите программу вычисления по длинам двух сторон треугольника и углу между ними длины третьей стороны и двух других углов.

5. Напишите программу для определения подобия

а) двух прямоугольников по двум смежным сторонам;

б) двух треугольников по трем сторонам.

(Указание: перед проверкой пропорциональности сторон надо их длины упорядочить по величине.)