§ 24. Организация данных в языке Бейсик

В программах на языке Бейсик можно пользоваться таблицами, прямоугольными и линейными. Прежде чем использовать в программе таблицу, надо дать машине указание, чтобы она заранее отвела в памяти место для нее. Такое указание дается командой DIM (сокращение английского слова DIMENSION - "размер"). В этой команде указывается имя таблицы, а также - в скобках - число ее строк и столбцов, например:

 10 DIM А (5,6)

или

 23 DIM В (23)

В первом из этих примеров определяется прямоугольная таблица А из 5 строк по 6 чисел в каждой; во втором примере определяется линейная таблица из 23 элементов. Одной командой DIM можно описывать несколько таблиц:

 10 DIM A (100), В (10,30), С1 (25)

Действие "Запросить таблицу" переводится в случае линейной таблицы, содержащей N элементов, следующим образом:

10 FDR I = l TO N 
20 INPUT A(I) 
30 NEXT X

Выполняя этот фрагмент, ЭВМ последовательно запросит N чисел, помещая их на соответствующие места в таблице. Для прямоугольной таблицы В, состоящей из N строк и К столбцов, перевод таков:

10 FOR I = 1 ТО N 
20 FOR J = l TO К
30 INPUT B (I, J) 
40 NEXT J 
50 NEXT  I

Здесь команды 10 и 50 последовательно перебирают номера строк таблицы. Команды 20, 30, 40 предназначены для ввода элементов очередной строки таблицы.

Действие "Сообщить таблицу" переводится на язык Бейсик аналогично, только вместо слова INPUT надо писать слово PRINT.

Запишем с комментариями программу вычисления суммы всех элементов линейной таблицы, состоящей из 20 чисел:

10 REM СУММИРОВАНИЕ ЭЛЕМЕНТОВ ТАБЛИЦЫ ИЗ 20 ЧИСЕЛ
20 DIM А(20)
30 REM ВВОДИМ ЭЛЕМЕНТЫ ТАБЛИЦЫ А
40 FOR I = 1 ТО 20
SO INPUT A(I)
60 NEXT I
70 REM БУКВОЙ 8 БУДЕТ ОБОЗНАЧЕНА СУММА
8O S = 0
90 REM ВЫЧИСЛЯЕМ СУММУ,  ДОБАВЛЯЯ К S ПО ОЧЕРЕДИ
ЭЛЕМЕНТЫ ТАБЛИЦЫ 
100 FOR I = 1 TO 20 
110 S = S + А (I) 
120 NEXT I
130 REM ПЕЧАТАЕМ РЕЗУЛЬТАТ 
140 PRINT"S = "S

Такие программы часто требуются при обработке данных наблюдений. А наблюдать можно что угодно. Например, каждый день вы ходите в школу и обратно. Сколько шагов вы делаете, преодолевая это расстояние? Если в течение нескольких дней вы из любопытства проведете подсчеты, то наверняка у вас получатся близкие друг другу, но все же разные числа. Никому, конечно, и в голову не придет, что меняется расстояние между школой и домом. Ясно, что на количество шагов влияют различные внешние факторы. Скажем, в школу вы шли быстро, чтобы не опоздать,- ваш шаг был шире, а по дороге домой вы шли не спеша, с одноклассницей - ваш шаг был короче. Можно сказать, что количество шагоз от школы до дома - величина случайная. Проведя двадцать наблюдений, вы получите двадцать значений случайной величины.

Например, пусть некий школьник И*** получил следующую последовательность чисел:

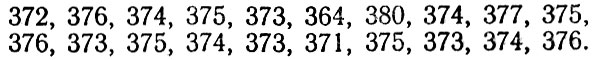
Их удобнее всего расположить в виде линейной таблицы. Какое же количество шагов естественно взять в качестве расстояния от школы до дома? Каждому ясно - среднее арифметическое. Для его вычисления можно применить только что записанную программу и затем результат разделить на 20. Получится 374.

Вычислить среднее арифметическое десяти чисел легко и без ЭВМ. Но когда речь идет об обработке сотен тысяч, а иногда и миллионов наблюдений, без ЭВМ не обойтись. Ведь и в нашем случае десять наблюдений дадут, по-видимому, довольно грубый результат. Чтобы оценить расстояние от дома до школы более точно, его надо пройти много раз.

Усредняйте значения - это убережет вас от ошибочных выводов!

Как же определить, насколько точно мы узнали расстояние, проведя то или иное количество наблюдений? Математики для этой цели ввели специальную величину и назвали ее дисперсией (от dispersion - "разброс"). Обозначим значения случайной величины а₁, ..., а_n, а среднее арифметическое этих значений - буквой М. Дисперсия - это среднее арифметическое квадратов разностей между значениями случайной величины и ее средним значением. В наших обозначениях

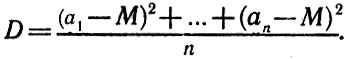
Из этой формулы видно, что чем меньше дисперсия, тем меньше

отличаются результаты наблюдений от своего среднего значения и тем ближе среднее значение к истинному. В частности, если D = 0, то все числа щ совпадают между собой (и со своим средним значением).

Дисперсия - главный свидетель разброса данных

Конечно, среднее значение числа шагов от дома до школы характеризует не только расстояние, но и длину шага человека: у разных людей и длина шага разная. Куда больше можно узнать о человеке, его характере, темпераменте и некоторых наклонностях, зная всю последовательность наблюдений.

Например, рассматривая приведенную выше последовательность, полученную И***, можно предположить, что значение 364 получилось в тот день, когда он опаздывал в школу. Вообще же характер у И*** довольно ровный, темперамент скорее флегматический - лишь один раз (получив, наверное, двойку) он шел заметно медленнее, чем обычно, сделав 380 шагов. Подумайте, что еще можно сказать об И***?

Допустим теперь, что И*** сагитировал нескольких своих товарищей провести тот же эксперимент. Через 10 дней каждый из них, в том числе и И***, представил по 20 результатов наблюдений, не указав своих фамилий. Можно ли узнать, какие из результатов принадлежат И***, а какие - нет? Да, можно!

Математики установили, что для этого, как правило, достаточно сравнить дисперсии и средние значения. Дисперсия и среднее значение почти так же индивидуальны, как отпечатки пальцев. Если наблюдения делал один и тот же человек, то дисперсии и средние значения будут близки, если разные люди, то далеки.

Осталось выяснить: какие значения считать близкими, а какие далекими? На этот вопрос дает ответ специальный раздел математики - статистика. Оказывается, достоверность ответа зависит от числа наблюдений. Если число наблюдений от 20 до 50, то дисперсии можно считать далекими, когда отношение большей дисперсии к меньшей больше 2. Чтобы говорить о близости средних значений двух последовательностей результатов, надо найти модуль разности средних и разделить его на квадратный корень из суммы дисперсий. Если полученное число больше 0,6, то средние значения считают далекими. В том случае, когда близки и дисперсии, и средние значения, можно сделать вывод, что наблюдения почти наверняка проводились одним и тем же человеком.

У любознательного ученика может возникнуть вопрос: откуда эти числа (2 и 0,6) взялись? Отвечаем: из специальных таблиц, которые были составлены математиками. Их можно найти в любом справочнике по математической статистике.

Метод сравнения средних значений и дисперсий используется в самых разных областях человеческой деятельности. В медицине - для установления диагноза, в литературоведении - для определения автора произведений, в криминалистике - для розыска преступников.

На лабораторной работе вы как раз и займетесь расследованием одного преступления.

Задача. Органами милиции задержан грузовик с помидорами, похищенными на овощной базе. В городе всего четыре овощных базы, каждая из них получает помидоры из своего сельскохозяйственного района. Определите, с какой базы были вывезены помидоры. Расследование осложняется тем, что помидоры на всех базах одного сорта.

Расследование

Воспользуемся методом средних значений и дисперсий. В каждом сельскохозяйственном районе свои условия произрастания помидоров, поэтому помидоры разных районов отличаются, скажем, удельным весом. Выберем по 20 помидоров (реально, конечно, их выбирается гораздо больше) на каждой овощной базе и из грузовика. У нас получится четыре последовательности по 20 значений в каждой (для каждой овощной базы) и еще одна (для грузовика), с которой мы и будем сравнивать первые четыре. Это наши исходные данные. Результатом является номер овощной базы, где совершено хищение.

Чтобы добиться этого результата, нужно, как рассказано выше, вычислить средние значения и дисперсии всех пяти последовательностей и провести сравнение. Напомним, что сначала сравниваются дисперсии, а затем для последовательностей, имеющих близкие дисперсии, сравниваются средние значения. Уже из сказанного ясно, что алгоритм будет достаточно сложным, так что мы построим его методом последовательной детализации.

Прежде всего организуем исходные данные. Последовательности для овощных баз и грузовика удобно записать в виде прямоугольной таблицы, имеющей 5 строк и 20 столбцов. Обозначим ее буквой А (последняя строка таблицы А соответствует грузовику). Тогда самая общая блок-схема выглядит так:

Блок-схема

Эта блок-схема показывает нам, что надо выделить вспомогательный алгоритм нахождения среднего значения и дисперсии 20 чисел, записанных в строке таблицы Л, а также алгоритм упорядочения двух чисел.

Алгоритм "Среднее значение". 
Аргумент k (номер строки таблицы А). 
Результат m (среднее значение). 
Присвоить 5 значение 0. 
Для каждого j от 1 до 20: 
Присвоить S значение S +A (k, j). 
Конец цикла по j. 
Присвоить m значение S/20.

Алгоритм "Дисперсия".
Аргумент k (номер строки таблицы A).
Результат d (дисперсия).
Присвоить S значение 0.
Для каждого j от 1 до 20:
Присвоить S значение S+(A (k, j) - C(k))2.
Конец цикла по j.
Присвоить d значение S/20.

Алгоритм "Упорядочение двух чисел". 
Аргументы х, у (числа, которые надо упорядочить). 
Результаты L, R (L - меньшее из чисел х и у, R - большее из них). 
Если x<Ly, то: 
Присвоить L значение х. 
Присвоить R значение у. 
Иначе:
Присвоить L значение у. 
Присвоить R значение х. 
Конец ветвления.

Основной алгоритм решения задачи выглядит так (части алгоритма, соответствующие разным блокам блок-схемы, отделены друг от друга):

Запросить таблицу A (5,20).
Для каждого i от 1 до 5:
Выполнить алгоритм "Среднее значение" при k = i
Присвоить С (i) значение m.
Конец цикла по i.

Для каждого i от 1 до 5:
Выполнить алгоритм "Дисперсия" при k = i.
Присвоить D (i) значение d.
Конец цикла по i.
Для каждого i от 1 до 4:

Выполнить алгоритм "Упорядочение двух чисел" при х = D(i), у = D(5).
Если R/L<2, то:       
Если |С(i) - С(5)|/√(D(i) + D(5))<0,6, то:
Сообщить "Номер базы".
Сообщить i.
Конец ветвления.
Конец ветвления.
Конец цикла по i

Переведите этот алгоритм на язык Бейсик.

Вопросы

1. Для чего нужна команда DIM?

2. Как переводятся на язык Бейсик команды "Запросить таблицу" и "Сообщить таблицу"?

Задания для самостоятельного выполнения

1. Переведите на язык Бейсик алгоритмы решения задач 3 - 10 из § 18 и 1 - 3 из § 19.

2. Найдите и исправьте ошибки в следующих программах.

а) Программа вычисления произведения элементов линейной таблицы

10 REM Ввод таблицы в  ЭВМ
20 FOR I = l ТО 100
30 INPUT A(I)
40 NEXT I
3Q FOR I = 1 ТО 100
60 S = S∗A(I)
70 NEXT I
80 PRINT S

б) Программа нахождения сумм элементов в каждой строке прямоугольной таблицы

10 DIM A(20,20)
20 FOR I = 1 ТО 20
30 PRINT "НАХОЖУ СУММУ ЭЛЕМЕНТОВ В "I" СТРОКЕ ТАБЛИЦЫ"
40 S = 0
50 FOR J = 1 TO 20
60 S = S + A (J, I)
70 NEXT J
80 PRINT "НАШЛА! СУММА РАВНА "S". ПЕРЕХОЖУ К СЛЕДУЮЩЕЙ
СТРОКЕ" 
90 NEXT I

3. Для нахождения максимального числа в прямоугольной таблице злоумышленником была составлена следующая программа:

10 DIM A(5,5)
20 FOR I = 1 ТО 5
30 FOR J = 1 ТО 5
40 INPUT A(I,J)
30 NEXT J
60 NEXT I
70 M = 0
80 FOR I = 1 TO 5
90 FOR J = l TO 5
100 IF M<A (I ,J) THEN M = A (I,J)
110 NEXT J
120 NEXT I
130 PRINT "МАКСИМУМ РАВЕН" М

Как и было задумано злоумышленником, ЭВМ, действуя по этой программе, далеко не всегда достигает цели. Требуется:

а) привести примеры таблиц, в которых ЭВМ найдет максимальное число;

б) привести примеры таблиц, в которых ЭВМ не найдет максимального числа;

в) исправить программу.

4. Дана квадратная таблица A, состоящая из п2 элементов, Напишите программу для вычисления:

а) суммы квадратов элементов, стоящих на диагонали, идущей из левого верхнего угла в правый нижний;

б) суммы квадратных корней тех же элементов.

5. В прямоугольной таблице с двумя строками по 10 чисел в каждой записаны координаты 10 точек (в первой строке - абсциссы, во второй - ординаты). Требуется:

а) найти максимальное расстояние между точками;

б) найти минимальное расстояние между точками;

в) составить таблицу всех попарных расстояний между точками.

6. В прямоугольной таблице записаны координаты 10 векторов. Определить:

а) какие из этих векторов перпендикулярны данному вектору;

б) какие из этих векторов параллельны данному вектору;

в) какие из этих векторов имеют ту же длину, что и данный вектор.

7. Проведите следующий эксперимент. Двадцать раз подбросьте монету и при выпадении "решки" записывайте 1, а при выпадении "орла" - 0. Получится последовательность из 20 нулей и единиц. Каковы среднее значение и дисперсия для этой последовательности? Повторите эксперимент. Получились ли новые среднее значение и дисперсия близкими к предыдущим?

8. Составьте математическую модель, алгоритм и программу решения следующей задачи.

Известны данные, показывающие продолжительность горения (в часах) электрических ламп, изготовленных на двух заводах. Лампы первого завода:

1600, 1510, 1610, 1520, 1650, 1530, 1680, 1570, 1600, 1700, 1720, 1680, 1800, 1780, 1690, 1710, 1630, 1720, 1750, 1810.

Лампы второго завода:

1580, 1460, 1640, 1550, 1600, 1620, 1700, 1640, 1750, 1820,

1660, 1740, 1760, 1730, 1590, 1610, 1650, 1700, 1580, 1670.

Можно ли утверждать, что на заводах поддерживаются одинаковые технологические условия производства?