§ 31. Электронные таблицы

В августе все готовятся к новому учебному году. И школьники, и учителя. Но особенно много хлопот у завуча: составляется расписание уроков. Завучу надо учесть большое количество разных факторов: требования учебного плана, пожелания учителей, количество учебных помещений и т. д. И вот расписание составлено. Однако заботы завуча на этом не кончаются. Вдруг оказывается, что заболел один из учителей или не закончен ремонт в одном из классов. Каждое такое ЧП требует переделки всего расписания. При этом завучу приходится заново учитывать большой объем данных и связей между ними.

С подобными задачами сталкиваются не только завучи. Диспетчерам при составлении графиков движения транспорта, бухгалтерам при составлении сметы, экспериментаторам при проведении серий опытов всем им приходится решать задачи, в которых изменение значения какого-то одного параметра требует пересчета большого числа результатов. И здесь компьютер готов сослужить добрую службу. Программистами уже созданы специальные программы - электронные таблицы. Электронная таблица позволяет хранить в табличной форме большое количество исходных данных, результатов, а также связей {математических соотношений) между ними. Но главное - при изменении исходных данных все результаты автоматически пересчитываются и заносятся в таблицу.

На лабораторной работе вы познакомитесь с учебной электронной таблицей и с ее помощью решите две задачи.

Если вычислений много, а времени мало, доверьтесь электронным таблицам

Задача 1. Чему будет равна численность населения СССР в начале третьего тысячелетия?

Численность населения

Сразу ясно, что задачу не решить, если не знать, как со временем будет меняться численность населения СССР. Иными словами, нам не обойтись без функции, выражающей зависимость численности населения от времени. Обозначим эту функцию f (t). Вы, конечно, ждете, что сейчас мы сообщим вам функцию f(t). Напрасно! Она нам неизвестна. Да и не может быть известной! Ведь народонаселение зависит от многих факторов: экологической ситуации, состояния медицинского обслуживания, морали и права и даже от международной обстановки.

Но огорчаться не стоит. Обобщив демографические данные, можно указать общий вид функции f (t):

Коэффициенты a, b для каждого государства свои. Конечно, эта формула лишь приближенно отражает реальность. Однако слишком большая точность и не нужна. Хорошо, если мы спрогнозируем численность населения с точностью до десятков миллионов.

Как же определить а и b? Идея состоит в том, что хотя а и b нам неизвестны, значения функции f(t) мы можем получить: достаточно заглянуть в статистический справочник "СССР в цифрах". В нем приведены данные о численности населения СССР (и других стран) за многие годы. Зная эти данные, можно подобрать an b так, чтобы значения f (t), вычисленные по формуле (1), не сильно отличались от данных справочника.

Поясним смысл слов "не сильно отличаться". Они означают, что максимальное отклонение теоретических результатов от фактических данных не должно быть слишком большим. Каждое из отклонений - это просто модуль разности двух чисел: фактического значения и значения, подсчитанного по формуле (1). Максимальное отклонение называют погрешностью. Итак, надо найти такие а и b, чтобы погрешность была наименьшей. Вспомните: похожим критерием мы руководствовались в § 15, когда добивались наиболее справедливого решения вопроса о расположении железнодорожной станции.

Подведем итоги. По сути дела, мы высказали упрощающие предположения, определили, что считать исходными данными и результатами. А именно: предположения состоят й том, что, во-первых, зависимость численности населения от времени выражается формулой (1) для некоторых постоянных а и Ъ и, во-вторых, значения а и Ь можно найти с достаточной точностью, Минимизировав погрешность. Предположение о постоянстве а и b естественно считать справедливым лишь для не очень большого промежутка времени, например двадцать лет. Поэтому за точку отсчета (t = 0) возьмем 1980 г. Исходные данные: сведения и статистического справочника за период с 1980 по 1987 гг. Результатами же являются значения а и b и численность населения СССР в 2000 г. (при t = 20).

Знаем мы и связь между исходными данными и результатами: сначала надо найти а и b, минимизируя погрешность (как ее находить, мы объяснили выше), а затем при этих а и b вычислить значение f (20). Правда, записать эту связь с помощью формулы нелегко. Еще труднее составить алгоритм поиска а и b (попробуйте!). На помощь приходят электронные таблицы. Как ими воспользоваться, мы расскажем на лабораторной работе.

А пока - еще одна задача.

Задача 2. Несколько человек решили организовать кооперативное видеокафе на 6 столиков по 4 места за каждым. С каждого посетителя будет браться плата за сеанс видеофильма и ужин (всем посетителям будет предлагаться один и тот же набор блюд). Предполагается, что по выходным видеокафе проводит по четыре сеанса в день, а в остальные дни - по два. Местный Совет народных депутатов постановил, что плата за вход не должна превышать 5 рублей. Требуется определить такую входную плату, при которой кооператив получит наибольшую выручку.

Кооперативное видеокафе

Казалось бы, здесь и решать нечего. Разве не ясно, что чем больше входная плата, тем больше выручка. Вот и ответ: входная плата должна быть 5 рублей. Очень часто планирующие органы подобным образом и поступают. Например, взвинчивают цены на ковры, надеясь таким образом увеличить доход от их продажи. Известно, к чему это приводит,- люди перестают покупать товары, и доходы резко падают. И в нашем случае, если сильно увеличить входную плату, то люди перестанут посещать кафе. Как видите, задача не так проста, "кавалерийским наскоком" ее не решить: нужна планомерная "осада".

Начать надо, как всегда, с построения математической модели. В чем были причины нашей неудачи? Мы предположили, что посещаемость не зависит от входной платы, и получили модель задачи, не соответствующую действительности. Значит, надо предполагать, что посещаемость зависит от входной платы. Обозначим входную плату через х. Тогда среднее число посетителей видеосалона является функцией от х. Обозначим эту функцию р (х). В задаче требуется найти такое значение х, при котором выручка, равная произведению входной платы на количество посетителей (т. е. хр (х)), достигает максимума. Если бы функция р (х) была известна, то найти требуемый максимум не составило бы особого труда (см. решение "железнодорожной" задачи из § 15).

Однако, как и в предыдущей задаче, функция р (х) нам неизвестна: ведь и посещаемость кафе зависит от многих факторов, например от репертуара, качества ужина и обслуживания. Пример предыдущей задачи подсказывает, что нужно иметь хотя бы общий вид функции р (х). Его можно указать, обобщив опыт работы подобных кафе:

Коэффициенты а, b и с для каждого кафе свои. Как же их определить? Проще всего найти значение с. Представьте себе невообразимое - в видеокафе пускают бесплатно (т. е. x = 0). Ясно, что свободных мест не будет. Следовательно, р (0) равно числу мест в кафе. С другой стороны, подставив 0 вместо х, получим р (0) = с. Значит, с равно количеству мест. В нашем случае с = 24 (шесть столиков по четыре места за каждым). Определить а и b так же просто не удастся.

По аналогии с предыдущей задачей мы могли бы найти значения а и by если бы знали несколько значений функции р (х). Данные о народонаселении мы смогли узнать из справочника. Справочников же по посещаемости видеокафе пока еще нет. Поэтому здесь требуется эксперимент.

Достаточно открыть кафе и установить на некоторый срок (дней десять) определенную плату за вход. Среднее число посетителей сеанса и даст нам (приближенно!) значение функции. Установив другую плату за вход, найдем приближенное значение р (х) при новом х, и так несколько раз. Тогда останется подобрать значения а и b так, чтобы погрешность (вспомните, что это такое) была минимальной.

Теперь уже нетрудно завершить построение модели (по образцу предыдущей задачи). Сделайте это самостоятельно.

Вопросы

1. Что такое электронная таблица?

2. Для решения каких задач полезно применение электронных таблиц?

Задание для самостоятельного выполнения

Постройте графики функций, задаваемых формулой (1), при значениях a, b и с, приведенных в следующей таблице:

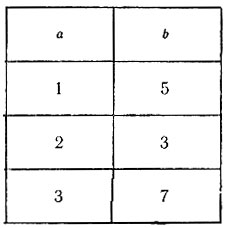
Данные

Как изменяется график:

а) при изменении а и постоянном b;

б) при изменении b и постоянном а?