§ 32. Пакеты прикладных программ

На предыдущих занятиях вы поработали с информационно-поисковой системой, редактором текстов, электронной таблицей. Понравилось? Удобно и быстро, не правда ли? Причем этими программами можно пользоваться, не зная их строения. Достаточно лишь разобраться в соответствующей инструкции. Важно и то, что с помощью каждой из программ: ИПС, электронной таблицы, редактора текстов можно решить не только одну конкретную задачу, но и целый класс задач, иногда очень непохожих друг на друга.

Специальные программы, предназначенные для решения классов задач из той или иной конкретной области, называютсяприкладными программами. Несколько взаимосвязанных прикладных программ называютпакетом прикладных программ (ППП).

Экономьте время - пользуйтесь готовыми пакетами прикладных программ

Пакеты прикладных программ освобождают специалиста, желающего воспользоваться помощью компьютера, от длительной и нелегкой работы по изучению языков программирования и от самостоятельного составления программ. Легко представить беспомощность пассажиров, которым предложили перед полетом изготовить самолет. В похожем положении оказалась бы огромная армия специалистов без такого мощного "оружия", как пакеты прикладных программ.

Затраты на создание сложных пакетов порой в несколько раз превышают стоимость самих ЭВМ. Сегодня уже недостаточно просто создать ЭВМ. Чтобы она могла приносить пользу, должно быть создано и программное обеспечение - пакеты прикладных программ для решения наиболее "популярных" классов задач. С некоторыми из этих классов задач вы уже познакомились: расчеты физических экспериментов (§ 3, 9, 21), задачи, решаемые методом Монте-Карло (§ 12), приближенное решение уравнений (§ 22), экономические задачи (§ 15, 19, 31), задачи обработки больших объемов данных (§ 29), задачи обработки текстов (§ 27, 30), задачи прогнозирования (§ 18, 23, 31) и т. д.

Пакетов прикладных программ разработано очень много: для расчетов траекторий спутников и параметров сложнейших технологических процессов, для решения проблем медицинской диагностики и управления каскадами гидроэлектростанций. Знакомые вам ИПС, редактор текстов, электронная таблица относятся к простейшим прикладным программам.

В этом параграфе речь пойдет еще об одной прикладной программе. Она называется "Оптима" и предназначена для решения задач планирования. Вспомните: одну из таких задач вы решали в § 19. В ней шла речь о производственном участке, выпускающем изделия двух видов: А и Б. Требовалось так спланировать выпуск этих изделий (x тыс. изделий А и у тыс. изделий Б), чтобы получить максимальную прибыль. Вы решали эту задачу, перебирая всевозможные натуральные значения x и у, удовлетворяющие пяти неравенствам. Реально при составлении планов приходится учитывать гораздо больше ограничений и для большего числа переменных. Простым перебором не обойтись: даже если использовать сверхбыстрые ЭВМ, оптимальный план пришлось бы искать слишком долго. Математики придумали специальные алгоритмы, позволяющие решать задачи планирования во много раз быстрее. Один из таких алгоритмов (он называется "Симплекс-метод") реализован в "Оптиме".

На лабораторной работе вы с помощью "Оптимы" решите следующую задачу. В ней идет речь о том же производственном участке, что и в § 19.

Задача. Начальник участка изучает возможность расширить ассортимент товаров - добавить к выпускаемым изделиям А и Б еще два вида изделий: В и Г. Предварительное изучение спроса показало, что можно реализовать не более 5 тыс. изделий В, получив при этом прибыль в размере 12 р. с каждого изделия. Можно также реализовать не более 6 тыс. изделий Г, получив прибыль 10 р. с изделия. На тысячу изделий В расход металла составляет 0,5 т, электроэнергии - 4 тыс. кВт-ч, рабочего времени - 5 тыс. часов. Для выпуска тысячи изделий Г требуется 1,5 т металла, 4 тыс. кВт⋅ч электроэнергии, 6 тыс. часов рабочего времени. Расширение ассортимента изделий потребует приобретения дополнительного оборудования на сумму 8 тыс. р. (в конце года она будет возмещена из прибыли участка). Можно ли спланировать выпуск товаров А, Б, В, Г так, чтобы получить прибыль большую, чем при выпуске только товаров А и Б (то есть целесообразно ли расширение ассортимента выпускаемых товаров) ?

Математическая модель этой задачи составляется так же, как в § 19. Вся разница - в количестве переменных (теперь их четыре) и количестве ограничений (их девять). Чтобы не использовать много различных букв, будем обозначать количества товаров А, Б, В и Г (в тыс. шт.) через x(1), х(2), x(3) и x (4).

Ограничения запишутся так:

(надо произвести не менее 2 тыс. изделий А);

(надо произвести не менее 3 тыс. изделий Б);

(нельзя израсходовать больше 32 т металла);

(нельзя израсходовать больше 54 тыс. кВт-ч электроэнергии);

(на участке работают всего 20 человек);

(нельзя реализовать больше 5 тыс. изделий В);

(нельзя реализовать больше 4 тыс. изделий Г);

(нельзя выпустить отрицательное число изделий). Прибыль подсчитывается по формуле:

Наша цель - составить такой производственный план (то есть найти такие значения х (1), х (2), х (3) и х (4)), который обеспечит максимальную прибыль. Таким образом, задача нахождения наилучшего производственного плана свелась к задаче определения максимального значения функции при некоторых ограничениях. Такие задачи называют задачами оптимизации, а функции, максимум (или минимум) которых надо найти,- целевыми функциями,

Решая задачу на ЭВМ с помощью "Оптимы" (как и с помощью электронных таблиц), достаточно построить математическую модель; ни алгоритм, ни программу составлять не потребуется.

Вопросы

1. Какие программы называются прикладными?

2. Для чего нужны пакеты прикладных программ?

3. Что такое задача оптимизации?

4. Какая функция называется целевой?

Задание для самостоятельного выполнения

Составьте математическую модель следующей транспортной задачи, записав систему ограничений и целевую функцию.

Задача. Бетон, производимый на заводах А и В, нужно развозить по трем стройплощадкам: N₁ N₂ и N₃. Известны потребности стройплощадок в бетоне, запасы бетона на каждом заводе и затраты на перевозку 1 тонны бетона от каждого завода до каждой стройплощадки. Требуется составить такой план перевозок, который обеспечивал бы наименьшие затраты.

Перевозка бетона

Лабораторная работа 19. Работа с прикладной программой "Оптима"

На экране дисплея - незаполненная таблица, а выше нее заголовок "Симплекс-метод" (см. рис. 47). Это значит, что в ваш персональный компьютер загружена "Оптима" и она ждет ваших указаний.

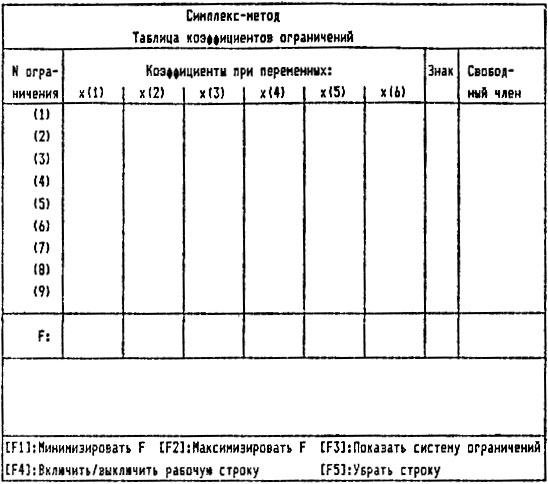
Рис. 47. 'Симплекс-метод'

Начать надо с заполнения таблицы. В строки, помеченные номерами, запишите коэффициенты линейных неравенств или равенств - ведь среди ограничений могут быть и равенства. Чтобы перемещать курсор по таблице, пользуйтесь клавишами со стрелками и клавишей "ПЕРЕХОД".

Ограничения вида х≥0в таблицу можно не записывать: "Оптима" заранее считает, что все переменные неотрицательны.

Исправить ошибки вы можете с помощью клавиши "УДАЛИТЬ СИМВОЛ". Если же строка вообще никуда не годится, сотрите ее, нажав клавишу <F5>.

Точно так же заполняется строка "F", в которой записываются коэффициенты целевой функции.

Последнее, что надо сообщить "Оптиме",- цель поиска. Что ей искать - максимум целевой функции или ее минимум? Нажав нужную функциональную клавишу, вы получите ответ: слева появятся оптимальные значения переменных, справа - значение целевой функции. Тут же "Оптима" вам напомнит, какое значение найдено - максимальное или минимальное.

Наверно, вам захочется посмотреть на набранные вами ограничения в привычном, "натуральном" виде. Нажмите клавишу <F3> - и система ограничений вместе с целевой функцией перед вами. Еще одно нажатие на <F3> - и перед вами снова таблица коэффициентов.

Теперь, разобравшись в этой несложной инструкции, приступайте к делу. Для начала найдите оптимальный план в задаче из § 19. Сравните время, затраченное вами на получение результата при помощи прикладной программы "Оптима", с тем, которое ушло на составление алгоритма, написание и отладку программы при выполнении лабораторной работы 10. Как видите, разница внушительная.

Пора приниматься за изучение возможностей расширения ассортимента выпускаемых товаров. Новая задача (см. § 32) отличается от только что решенной количеством переменных, числом ограничений и целевой функцией. Произведите эти изменения и получите ответ. Так стоит ли расширять ассортимент?..

Жизнь, однако, не стоит на месте. Каждый день приносит что-нибудь новенькое. Представьте себе - от ваших смежников пришла телеграмма, что из 32 т металла они решили 24 т передать другому предприятию, а на вашу долю оставить только 8 т. Тут уж не до прибыли, лишь бы госзаказ выполнить! Замените 32 на 8 и посмотрите, какой ответ вам даст компьютер. "Система ограничений несовместна",- напечатает он. Это означает, что нет таких значений переменных, которые удовлетворяют всем ограничениям. Похоже, что по вине смежников вам не удастся выполнить госзаказ,- металла не хватит. А какое минимальное количество металла необходимо? Надеемся, что "доводы" вашей ЭВМ окажутся убедительными для смежников и вы получите металл в достаточном количестве.

Решив задачу 1, вы составили математическую модель транспортной задачи. Найдите оптимальный план перевозок при следующих исходных данных:

потребности стройплощадок в бетоне: N₁ - 200 т, N₂ - 280 т, N₃ - 220 т;

запасы заводов: А - 320 т, В - 380 т;

таблица затрат на перевозку одной тонны бетона:

Не правда ли, это очень просто и удобно - пользоваться "Оптимой" для решения задач планирования?