7. Стратегия, риск и решение

"Быть или не быть? - вот в чем вопрос". Популярность этого вопроса связана прежде всего с тем, что каждый из нас неоднократно ставил его перед собой, мучился и решал так или иначе, с тем или иным успехом. Гамлетовские сомнения обуревали нас лишь в том случае, когда выбор того или иного варианта (быть или не быть) был связан с риском нарваться на неприятности. Вспомним, в каком смешном положении оказался бы Гамлет, если бы косвенные улики не оправдались и его дядя не оказался бы убийцей отца. В этом случае трагедия превратилась бы в фарс, чего Шекспир допустить не мог. Автор в данном случае не настаивает на подобной трактовке, но подчеркивает, что выбор Гамлетом одной из возможностей грозит ему неприятностями.

Дело в том, что из всех вариантов часто только один является правильным. Но выбрать его мешает недостаток информации. Если бы в нашем распоряжении всегда имелись необходимые сведения, то Гамлет с его вопросом был бы так же смешон, как человек, глубокомысленно решающий проблему изобретения велосипеда в наш космический век. Но со времен Шекспира информационный голод только обострился. Информация, правда, стала несколько более доступной (так, по телефону 09 можно получить несколько битов), но и вопросов задается во много раз больше.

Ко всему этому неизбежные случайные помехи искажают и обесценивают поступающую информацию. (Вспомним, что такой искажающей "помехой" для Гамлета были его бывшие друзья Розенкранц и Гильденштерн.)

Если учесть все сказанное, то следует проникнуться уважением к Гамлету, который блистательно поставил и решил одну из сложнейших ситуаций и разоблачил своего дядю.

Однако ни Гамлет, ни Шекспир не оставили рецепта принятия решения в обстановке помех. В данном конкретном случае мы знаем, как разоблачить дядю. Но ведь в жизни одна и та же ситуация почти никогда не повторяется! Как быть в любой другой обстановке?

Так быть или не быть?! Увы, Шекспир нам не дал ответа. Ответ дала статистическая теория решений.

Сказка о добром молодце и дорожном камне

Классическая ситуация, на которой можно почувствовать всю остроту задачи по принятию решения, хорошо известна всем с детства из сказок. Формулируется она следующим образом (автор не претендует на точность воспроизведения).

Добрый молодец подъезжает на своем могучем коне к развилке, где дорога разветвляется на три. Ни милиционера, ни прохожих - спросить некого. Надпись на придорожном камне вещает:

"Направо поедешь - коня потеряешь, прямо поедешь - голову потеряешь, налево поедешь - горе найдешь". И добрый молодец невольно тянет руку под шлем - почесать затылок, где люди часто ищут и иногда находят ответы на самые сложные вопросы.

Нашему молодцу нужно сделать выбор одной из четырех возможностей; то есть имеет в своем распоряжении четыре стратегии поведения.

Стратегия № 1. Поехать по первой дороге и, возможно, при этом потерять коня.

Стратегия № 2. Поехать по второй дороге и, возможно, лишиться головы.

Стратегия № 3. Поехать по третьей дороге и, возможно, горевать.

Стратегия № 4. Вернуться назад.

Реализация любой стратегии не представляет труда - дал шпоры коню и поехал. Но как найти правильное решение и что вообще назвать правильным (оптимальным) решением в такой ситуации? Если бы хоть одна из представленных возможностей гарантировала бы приятную перспективу, например встретить красавицу принцессу или, на худой конец, спящую красавицу, которую нужно разбудить! А то что ни дорога, го сплошные неприятности! Как быть?

Но наш добрый молодец, кроме традиционных коня, копья, меча и лука со стрелами, имеет еще и здравый смысл ("ума палата"). Пораскинув этим умом, приходит к мысли, что в сложившейся ситуации "не до жиру" и нужно принимать такое решение, которое представит ему меньше всего неприятностей. Народную мудрость "из всех бед выбирай меньшую", как видно, и определяет интуитивный, но совершенно правильный подход молодца к выбору оптимального решения. Этим сделал много: выбрал решающее правило, то есть определил, каким образом будет приниматься наилучшее решение. Это правило гласит: наилучшее решение должно принести минимум неприятностей.

Но для реализации этого решающего правила ему нужно определить, как измерять неприятности при выборе той или иной возможности, то есть нужно знать, в каких единицах измеряются неприятности, и определить, сколько единиц неприятностей принесет каждая возможность, если ее выбирать.

Итак, размышляет наш молодец, если верить надписи на камне, то из создавшегося положения есть только четыре выхода:

1. Терять коня, если ехать по первой дороге.

2. Терять голову, если ехать по второй.

3. Горевать, если ехать по третьей.

4. Опозориться и потерять престиж, если возвращаться назад.

"А буду я считать ущерб, наносимый мне, - рассуждает молодец, - числом врагов, которых я не смогу победить. Конь мой в битве затопчет четверых, значит, потеря коня грозит мне ущербом в 4 единицы. Сам я могу справиться с семерыми, следовательно, при потере головы мой ущерб измеряется 11 единицами (семь моих и четыре коня; ведь без меня конь не станет топтать врагов, еще не приучен)".

Горе по-разному действует на людей. Наш молодец решил, что горе сделает неверной его руку и число побежденных врагов в этом случае уменьшится до трех. Тогда ущерб при выборе третьей дороги измеряется 3 единицами.

Возврат назад означает малодушие, потерю престижа, а вместе с ним и воинского звания, что для молодца почти эквивалентно потере головы. Следовательно, и в этом ущерб равен 11 единицам.

Так оценил свой ущерб добрый молодец, полагая, что камень вещал вправду. А если он, камень, грубо говоря, соврал? Ведь бывает такое, и не только в сказках! (Все та же помеха!) Тогда величины ожидаемого ущерба будут иными.

Наш молодец - человек бывалый. Он много скитался, да и понаслышан был немало, и может оценить достоверность получаемой информации. Его опыт свидетельствует, что в сказках придорожные камни-указатели склонны преувеличивать опасность и особо грозным надписям следует доверять лишь наполовину. А сейчас сам должен определить свое отношение к "каменным" заявлениям.

Поразмыслив как следует, решает приписывать нуль тому, чему вообще не верит, и единицу тому, что заслуживает полного доверия. Все промежуточные числа определяют степень "правдивости" камня и дают возможность знать степень уверенности в том, что предсказание сбудется.

Так молодец определил правдивость для первой стратегии (потеря коня) - 0,6, для второй (потеря головы) - 0,4, для третьей (горе) - 0,9 и для четвертой (отступление) - 1,0 - престиж при малодушии теряется наверняка.

Здесь мы подходим к самому важному понятию - к риску, связанному с принятием оптимальных решений. Величина риска решения определяется как возможным ущербом, наносимым этим решением, так и очевидностью, с которой ущерб наносится. Если маловероятно, что произойдет неприятность, то риск мал. Мал и в том случае, если вероятность ущерба велика, но сам по себе ущерб мал.

Задумывались ли вы, например, над тем, почему мы выходим из дома в дверь, а не в окно?

А дело все в риске. Риск свернуть себе шею, пользуясь окном вместо двери, значительно больше риска при выходе в дверь. Конечно, и выходя в дверь, мы можем споткнуться и расквасить себе нос, скатившись с лестницы. Но мы знаем, что и ущерб при этом невелик, мала и вероятность такой неприятности.

Выходя в окно, также можно избежать всяких неприятностей, но это маловероятно. Да и неприятности (если и случатся) будут слишком велики. Тогда, пролетая мимо ок соседей, можно смело отказываться от приглашения на ужин, так как риск будет очень большим и рассчитывать на благоприятный исход можно, но явно нецелесообразно.

Именно эти соображения лежат в основе выбора наилучшей стратегии выхода на улицу. Люди интуитивно поняли это и стелют коврик для вытирания ног у входной двери, а не у подоконника.

Как видно, риск равен произведению ущерба на вероятность того, что этот ущерб произойдет.

Если, например, единичный ущерб происходит лишь в половине всех случаев (вероятность равна ¹/₂), то риск такого решения равен половине:

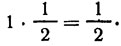
Риском является средний возможный ущерб.

Вернемся к нашему молодцу. Чтобы определить риск, на который идет при выборе той или иной стратегии, нужно умножить ущерб на степень уверенности, что такой ущерб произойдет. На рисунке 34 показаны последовательно ущербы, степени уверенности (вероятности) и риски для всех четырех стратегий, которыми располагает молодец. Видно, что наилучшей (оптимальной) стратегией является стратегия с минимальным риском.

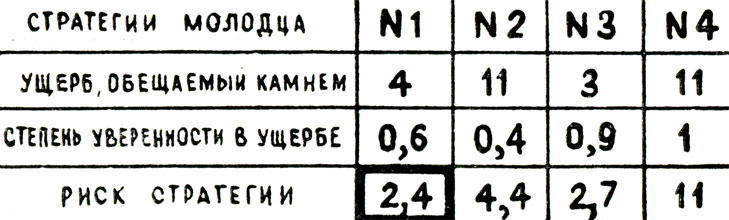
Рис. 34

В самом деле, минимизируя риск, мы тем самым можем быть уверены, что в среднем наш ущерб будет минимальным. Это вовсе не означает, что действительный ущерб не сможет быть больше. Однако может оказаться и меньше среднего. Поэтому рассчитывать следует на средний ожидаемый ущерб. Его и нужно минимизировать.

Теперь выбор дороги сводится к определению стратегии с минимальным риском. Такой стратегией в данном случае оказывается стратегия № 1 - ехать по дороге, идущей вправо, и рисковать конем. Действуя подобным образом, наш воин поступает оптимально, в данной ситуации подвергается минимальному риску. Это вовсе не значит, что идет на потерю коня, вовсе нет. Дело в том, что, судя по прошлому опыту, потеряет лишь с вероятностью 0,6, а уверенность в собственных силах дает ему право рассчитывать на благополучный исход.

Итак, наш добрый молодец выбрал наилучшую стратегию. Как видно, в этом ему помог его опыт, иначе не смог бы оценить достоверность камня. А что, если этого опыта нет? Что, если впервые выехал? Тогда ему ничего не остается, как в равной степени верить или не верить всем надписям. В первом случае, когда наш герой явно является пессимистом (этот случай показан на рисунке 35), оптимальной стратегией является самая осторожная стратегия № 3 (горевать). Она обеспечивает ему минимальный риск в соответствии с его пессимистическими представлениями о правдивости камня. Во втором случае (ни во что плохое не верить) все стратегии, кроме четвертой, имеют нулевой риск и для него в равной степени хороши. Оптимальное поведение заключается в произвольном выборе одной из трех дорог. Такая небрежность характерна для оптимиста.

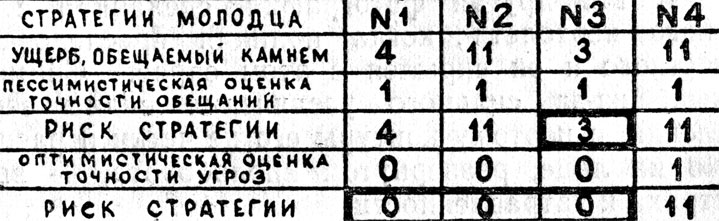
Рис. 35

Все указанные рассуждения нашего молодца вполне просты и естественны. и они лежат в основе теории статистических решений, которая помогает преодолевать случайность нашего мира.

А теперь из волшебной детской сказки перенесемся в суровую взрослую область - криминалистику.

Он или не он! (Детектив)

...Инспектор Мегрэ вздрогнул. За шиворот попала большая холодная капля осеннего дождя. Другая капля скользнула по стволу пистолета и, на мгновение задержавшись у мушки, повисла на дуле. Мегрэ стряхнул ее и со вздохом сунул пистолет в карман. Кивнув сержанту, чтобы тот продолжал наблюдение за сараем, усталой походкой зашагал к автомобилю.

"Черт бы побрал этого парня, - думал Мегрэ. - Приходится торчать здесь в такую мерзкую погоду вместо того, чтобы потягивать свежий кофе у камина и листать еженедельник!"

В машине шофер протянул ему термос. Мегрэ поморщился, представив, во что превратился кофе, но выпил теплую жидкость и поблагодарил.

В который раз положил на колени две фотографии и стал их изучать. Одна из них была из полицейского досье. На ней широко и самодовольно улыбался уже немолодой мужчина с наглыми глазами и каменным подбородком. "Такой выстрелит всегда первым и... последним", - подумал Мегрэ. Впрочем, это не было написано на физиономии молодчика - просто инспектор его хорошо знал и уже несколько лет следил за его "подвигами". Откровенный фашист, член террористической офицерской организации, бывший коллаборационист, связанный, по слухам, с гестапо и т. д. хорошо знает, что его ждет гильотина, и, наверно, поэтому наглеет год от года.

А вот другая фотография, сделанная с полицейского вертолета, когда полиция преследовала неизвестного и скрылся в этом сарае. Снимок скверный, из-за сильного увеличения видна зернистость пленки, и поэтому контуры его не четки и расплывчаты. Но на лице, развернутом вполоборота, - выражение страха и затравленности.

Как важно знать: один и тот же человек изображен на обеих фотографиях или разные? Ведь от этого целиком и полностью зависит все дальнейшее поведение, а возможно, и жизнь многих людей.

Если обе фотографии сделаны с одного и того же лица, то осаду сарая следует вести с особой тщательностью - от этого типа можно ждать всего: и снайперских выстрелов, и гранат (недаром же так рвался к этому сараю, когда понял, что не уйти от погони, - здесь, наверное, есть склад оружия).

Если же на фотографиях изображены разные лица, то дело терпит. Можно спокойно договориться с парнем в сарае, попытаться убедить его прекратить сопротивление и не усугублять свою вину. Да и отстреливается как-то странно, будто старается испугать.

Так "он" или "не он"? - вопрос, который задавал себе инспектор Мегрэ все это утро, но ответа не получал. На фотографиях почти все было разное: и размер, и ракурс, и четкость, и мимика. Но это мог быть один и тот же человек!

На все запросы инспектора специалисты отказывались дать ответ - слишком сильно различались фотографии. Правда, слышал, что подобные задачи решают на вычислительных машинах, но, как всегда, времени зайти и поговорить с кибернетиками не было, да и под старость совестно было идти учиться.

"А, видно, придется", - подумал Мегрэ и решил связаться с вычислительным центром.

На этом мы простимся со знаменитым сыщиком.

Дальше не будет ни выстрелов, ни погони, а детективное начало понадобилось автору как эффектная завязка, необходимая во всякой популярной книге, если она популяризует не очень популярные вещи.

Рассмотрим вполне реальный пример. Речь пойдет о такой ответственной в криминалистике операции, как опознание преступника.

Следователь в своей работе почти на каждом шагу сталкивается с проблемой: по имеющимся сведениям о преступнике надо установить, является ли им подозреваемое лицо или нет. Рассмотрим для простоты случай, когда имеются фотокарточки преступника и подозреваемого. Нужно ответить: один и тот же или разные люди представлены на фотографиях?

Итак, он или не он?

Не торопитесь отвечать на вопрос, он не так прост, как кажется. Давайте прежде проанализируем создавшееся положение.

Следователю нужно принять решение и выбрать одну из двух возможностей: "он" и "не он", то есть "преступник и подозреваемый являются одним и тем же лицом" и "разными лицами". Следователь, анализируя фотокарточки, должен прийти к какому-то решению, причем это решение должно быть в определенном смысле наилучшим.

А что значит наилучшим? Процесс следствия, как и всякий другой реальный процесс, подвержен действию случайных помех, мешающих выбору правильного решения. Такие помехи возникают в результате низкого качества сопоставляемых фотографий, искажений, вносимых оптической системой фотоаппарата, различных разворотов лиц, разной мимикой и т. д. Как видно, эти искажения не могут быть "исправлены" на фотокарточке и являются помехами, с которыми надо считаться. Присутствие их может привести к ошибкам следствия. Эти ошибки бывают разного рода.

Ошибки, которые приводят к оправданию виновного, назовем ошибками первого рода. У следователя были фотографии одного и того же лица, но помехи были настолько велики, что лица на представленных фотографиях ему показались разными и он сделал ошибку. В результате этой ошибки преступник ускользнул.

Но существуют и другие ошибки. Лица на фотографиях были разные, но очень похожие, и следователь ошибочно решил, что эти фотографии сделаны с одного и того же лица. В этом случае страдает невиновный, которого приняли за преступника. Такого характера ошибки назовем ошибками второго рода.

Оба вида ошибок нежелательны, ибо они приносят определенный ущерб отдельным лицам, престижу суда и в конечном счете обществу. Так, в первом случае (оправдание виновного) ущерб заключается в том, что преступление не наказано, преступник остается на свободе и сможет совершить новое преступление.

Во втором случае (осуждение невиновного) преступник также остается ненаказанным, но, кроме этого, страдает невиновный человек. Как видно, такая ошибка тяжелее и приносит больший ущерб обществу. (Вспомним известную фразу: "Лучше оправдать виновного, чем осудить невиновного".) Но это вовсе не означает, что следует оправдывать всякого подозреваемого.

Следователь это хорошо понимает и, принимая решение, старается свести к минимуму ущерб, который будет нанесен обществу при ошибочном решении.

Пусть ущерб от оправдания виновного выражается некоторым числом А, а ущерб от осуждения невиновного определяется числом В. Тогда очевидно, что ошибка первого рода приводит к ущербу А, а ошибка второго рода - к ущербу А+В.

Трудно сказать, в каких единицах измерять эти ущербы. Но при внимательном рассмотрении в этом нет особой необходимости - достаточно определить, во сколько раз один ущерб превышает другой, то есть задать число

В самом простейшем случае достаточно считать А=В (q=2), то есть предполагать, что ущерб, наносимый следствию от осуждения невиновного, в два раза больше ущерба от оправдания виновного. Дальнейшее уже не зависит от конкретных значений А и В.

Пусть следователь в процессе сопоставления фотокарточек пользуется каким-то определенным правилом (алгоритмом), позволяющим вычислить степень несоответствия обоих изображений. Обозначим эту степень некоторым числом Q. Чем больше получается это число, тем более разными представляются лица, изображенные на фотографиях. И наоборот, чем меньше - тем они более схожи. Если бы не было помех, то задача была бы решена просто: лица одинаковые, если Q=0, и разные при Q>0. Но вот помехи! Может оказаться, что за счет помех Q=0, а лица разные, и наоборот. Как же быть, какое принимать решение?

Для этого нужно построить решающее правило. Это правило звучит крайне просто. Если величина несоответствия Q больше некоторого числа τ, то лица предполагаются разными и подозреваемый невиновен. Если же Q меньше τ, то на фотографиях изображено одно и то же лицо.

Но как определить величину τ? Оказывается, что успех следствия во многом зависит от этого числа. Пусть τ мало (или вообще равно нулю). Тогда в соответствии с указанным решающим правилом мы почти никогда не осудим невиновного. Но если подозреваемый и есть преступник, то мы оправдаем и наверняка совершим ошибку первого рода. Значит, при слишком малом τ невиновный осужден не будет, но преступник почти наверняка ускользнет.

Пусть т велико. В этом случае преступник, если он будет подозреваться, не уйдет. Но если подозреваемый окажется невиновным, то в соответствии с решающим правилом мы обязаны его осудить, а преступник останется на свободе. Ущерб следствию будет еще больше (А+В).

Отсюда хорошо видно, что значение τ должно быть каким-то промежуточным, чтобы минимизировать ущерб, наносимый следствию в результате возможной ошибочной экспертизы.

Но как все-таки определять значение τ? Здесь на помощь следователю и приходит теория статистических решений.

Нужно составить функцию риска экспертизы. Эта функция имеет простой вид:

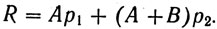
Здесь А и В, как сказано выше, - ущербы от оправдания виновного и осуждения невиновного, р₁ - вероятность оправдания виновного, то есть степень уверенности в том, что произойдет ошибка первого рода, р₂ - вероятность осуждения невиновного, то есть степень уверенности в том, что произойдет ошибка второго рода.

Функция риска характеризует, таким образом, средний ущерб в случае ошибочной экспертизы.

Значения вероятностей р₁ и р₂ зависят от числа т. На рисунке 36 показаны эти зависимости. Ясно, что при τ=0 наверняка произойдет ошибка первого рода (р₁=1), так как тогда оправдывается виновный. А при слишком большом τ наверняка будет сделана ошибка второго рода, потому что будет осужден невиновный (р₂=1).

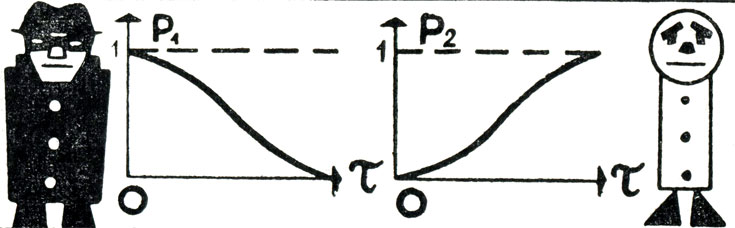
Рис. 36

Если теперь мы подставим эти выражения в формулу для риска, то получим зависимость риска следствия от величины τ. Она показана на рисунке 37.

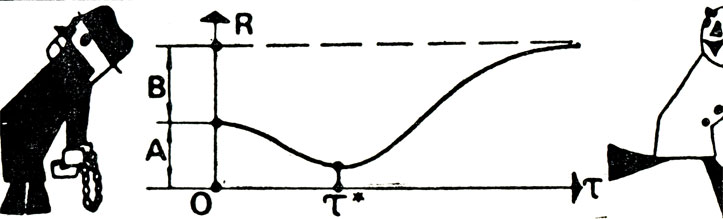
Рис. 37

Хорошо видно, что риск имеет отчетливо выраженный минимум при τ^*! Там-то и нужно искать оптимальное значение τ. Следовательно, для оптимальной экспертизы нужно выбрать τ=τ^*, и риск следствия в этом случае будет минимален. Поступая так, следователь может быть уверен, что в случае ошибки причиненный ущерб в среднем будет наименьшим.

Следует обратить внимание, что при этом нас не интересует сама величина риска. Важно, чтобы она была минимальной. А каков этот минимум - для процедуры выбора τ^*, как видно, несущественно. Это обстоятельство значительно облегчает задачу, так как снимает необходимость определения величин А и В, которые (увы!) мы в настоящее время не умеем не только вычислять, но и высказать о них какие-либо разумные соображения.

Действительно, пусть, например, А=В, то есть ущербы одинаковы. Тогда из формулы для риска получаем:

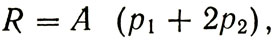
откуда хорошо видно, что положение минимума риска не зависит от А. (Величина А будет определять величину риска, но не положение его минимума.)

Таким образом, минимизация риска путем соответствующего выбора параметра τ позволяет следователю преодолеть влияние случайных помех, возникающих в процессе опознания преступника.

А теперь поговорим о вполне реальных и близких нам вещах... о газированной воде и сомнениях автомата, ее продающего.

Ему также приходится иметь дело со случайными помехами и принимать оптимальное решение в этой обстановке.

Быль об автомате, продающем газированную воду

Простейшим примером технического устройства, принимающего решение, является обычный автомат для продажи газированной воды. Получив трехкопеечную монету, автомат прежде всего должен выяснить: а монета ли это? (Быть или не быть?) В его распоряжении имеется две стратегии, соответствующие двум возможностям:

Стратегия № 1 - "быть" - принять монету, то есть признать ее доброкачественной и напоить ее владельца.

Стратегия № 2 - "не быть" - признать монету недоброкачественной и вернуть ее владельцу.

Для принятия решения автомат должен "поставить эксперимент" с целью проверки качества монеты. Пусть он заключается в измерении диаметра монеты. Автомат располагает двумя калибрами: верхним и нижним. Монета должна проходить в верхний калибр и одновременно застревать в нижнем. Только в этом случае она будет признана доброкачественной.

Верхний калибр проверяет, не превышает ли размер монеты пределы, указанные стандартом. Если превышает, то монета попросту не попадает в автомат. В этом случае монета признана автоматом некачественной, и проситель получает отказ.

Нижний калибр сортирует поступающие монеты на два класса. В первый класс относятся монеты, размер которых больше размеров калибра, - они будут задержаны и признаны доброкачественными. Второй класс монет имеет меньший размер. Эти монеты проскочат калибр и будут возвращены их владельцу как недоброкачественные.

Проектировщик автомата должен выбрать размеры этих калибров. Размер верхнего определить нетрудно - он должен быть равен размеру новой монеты d. Почему новой? Да ведь со временем монета не становится больше, и все доброкачественные монеты имеют размер не больше первоначального.

Значительно труднее установить размер нижнего калибра. Если его сделать слишком близким к верхнему, то старые, истертые, но качественные монеты будут автоматом приниматься за некачественные. Если же этот размер сделать слишком малым, то автомат будет принимать и фальшивые монеты, то есть суррогаты. В обоих случаях автомат будет терпеть ущерб: в первом - от потери клиента и своего престижа в глазах этого клиента, а во втором - оттого, что за воду не было заплачено (точнее, заплачено суррогатом).

Как видно, размер нижнего калибра должен быть оптимальным, в определенном смысле наилучшим. Нетрудно заметить, что этот размер должен минимизировать средний ущерб, наносимый ошибками первого и второго рода, должен свести риск к минимуму.

Ошибкой первого рода назовем непризнание качественной монеты, например монета была хорошей, но случайно несколько истертой и автомат не принял ее (осуждение "невиновного"). Ошибкой второго рода следует назвать прием автоматом некондиционной монеты (оправдание "виновного"). Пусть d - стандартный размер монеты, a d-τ - размер нижнего калибра. Тогда вероятности ошибок первого и второго рода будут зависеть от величины τ так, как показано на рисунке 36. При τ=0 размеры обоих калибров совпадают и автомат не делает вообще ошибок второго рода и не принимает некачественных монет. Но в этом случае он наверняка будет делать ошибки первого рода, то есть будет отклонять и хорошие монеты. Если величину τ выбрать достаточно большой, то ошибки первого рода делаться почти не будут, и автомат будет принимать хорошие монеты, но вместе с ними он будет принимать и некачественные, и тем самым увеличится возможность совершения ошибок второго рода.

Чтобы определить оптимальное значение этой величины, конструктор должен построить функцию риска и выбрать такое τ, которое минимизирует риск автомата. Для этого ему нужно ввести величину ущерба от ошибок первого рода - число q₁ и величину q₂ - ущерб от ошибок второго рода. Формула функции риска автомата выглядит так:

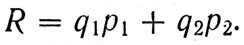
Пусть для простоты q₁=q₂=q, то есть ущерб от ошибок обоего рода признан одинаковым. Тогда

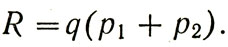
На рисунке 38 показана зависимость риска от величины τ. Хорошо видно, что значение τ^* минимизирует риск автомата. Это значение и должен назначить конструктор при проектировании. И тогда риск неправильного решения автомата будет минимален и автомат будет принимать оптимальные решения.

Любопытно, что в этом случае τ^* не зависит от величины ущерба q: различные значения q будут изменять величину риска, но положение его минимума будет неизменно. Следовательно, конструктор может для риска пользоваться формулой:

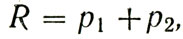
что значительно упрощает его задачу.

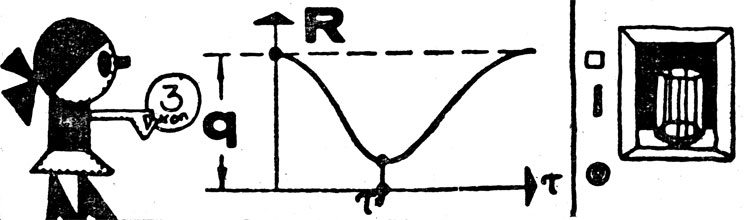
Рис. 38

Заканчивая разговор о решениях и риске, заметим лишь, что идея введения риска чрезвычайно плодотворна не только в криминалистике и технике, но и физике, биологии, экономике и других науках. Всякий раз, принимая оптимальное решение в случайной обстановке, нужно оценивать его риск и стараться свести этот риск к минимуму. Поступая так, мы делаем наши выводы наиболее обоснованными, несмотря на случайные помехи, то есть преодолеваем случайность и снижаем ее разрушительное действие.

Право на ошибку

Мы живем в случайном мире, где ничего нельзя утверждать со стопроцентной уверенностью и все суждения должны начинаться словами: "по всей вероятности..." Иначе всякое категорическое утверждение рискует случайно не оправдаться. Действующие случайные помехи создают такой шумовой фон, такие условия, в которых трудно не ошибаться.

В предыдущих параграфах мы рассмотрели способы борьбы со случайными помехами. Эта борьба, как всякая борьба, имеет свои жертвы и потери. В борьбе со случайными помехами теряется самое дорогое и невозвратимое - время. Как было показано выше, лучшим средством для преодоления случайности является накопление. А всякое накопление происходит во времени, которое и образует потери.

Рассмотрим следующую весьма распространенную ситуацию. Пусть нам предстоит принять какое-то решение, сделать выбор из нескольких возможностей. Например, выбрать место для отдыха в одном из трех городов: Одессе, Ялте и Сочи. Прежде чем принять решение, следует собрать необходимую информацию. Эта информация, как правило, бывает весьма зашумленной, со всякого рода помехами. Так, спрашивая своих знакомых о жизни и удобствах в интересующих городах, вы можете получить весьма противоречивые ответы. Один устроился плохо, но зато познакомился на пляже с девушкой, влюбился. Конечно, он будет с жаром хвалить свое место отдыха. Другой, наоборот, устроился великолепно, но... поссорился с женой, и она даже собиралась уехать до окончания отпуска. Этот, разумеется, будет плохого мнения о хорошем месте отдыха.

Чтобы правильно решить, нужно "отфильтроваться" от помех в получаемой информации. Это можно сделать, например, таким образом. Отведите три странички своего блокнота для сбора информации об отдыхе в этих городах и ставьте плюс, если отзыв положительный, и минус, если отрицательный. Только позаботьтесь, чтобы все отзывы были от разных людей и таких, мнению которых вы доверяете.

Перед тем как покупать билеты, загляните в блокнот и обработайте полученную информацию. Результаты обработки будут иметь, возможно, такой вид:

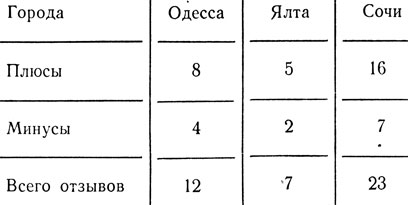
Результаты обработки

Как быть дальше? Наверное, прежде всего нужно договориться о решающем правиле. В качестве такого правила естественно выбрать следующее: поедем отдыхать в тот город, который имеет наибольший процент положительных отзывов. Из указанной таблицы легко получить:

Одесса - 66 процентов, Ялта - 71 процент, Сочи - 69 процентов.

Получается, что наибольший процент имеет Ялта. Значит ли это, что, поехав в Ялту, вы не ошибетесь?

Разумеется, нет!

Дело в том, что полученные проценты - приближенные числа и верить им следует неодинаково. Действительно, эффективность осреднения зависит от его объема: чем больше объем, тем точнее результат. Поэтому самой точной оценкой была оценка Сочи (23 отзыва), а самой приближенной - Ялта (7 отзывов). И выходит, делая ставку на Ялту, можно легко ошибиться, так как вполне возможно, что, получив дополнительную информацию, то есть увеличив число отзывов о Ялте до 23, мы получим снижение этого процента, например, до 67. А это изменит наш выбор, и придется брать билеты до Сочи (69).

Как же быть? Говоря строго, для вполне надежного принятия решения нужно собрать такой значительный объем информации и соответственно пойти на такие большие временные затраты, которые мы не можем себе позволить (придется отложить отдых до следующего сезона). Именно поэтому, принимая решение, мы всегда ограничиваемся разумными затратами, но всегда с определенной вероятностью, что это решение может оказаться неверным.

Можно ли указать на оптимальный объем сведений, который необходимо собирать, чтобы решить ту или иную задачу? Оказывается, можно.

Для этого прежде всего надо определить потери. В этом случае потери имеют двоякий характер.

Это прежде всего потери на сбор информации (например, при накоплении). Пусть для простоты эти потери W пропорциональны времени Т (вспомним известную формулу: "время - деньги"). На рисунке 39 этот вид потерь показан наклонной прямой, которая означает, что потери на сбор информации линейно зависят от времени.

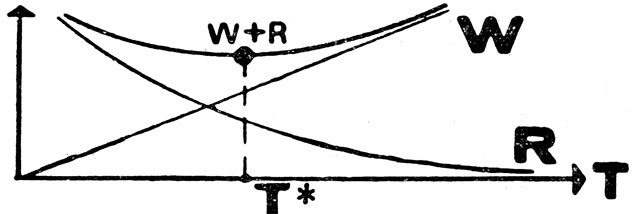
Рис. 39

Теперь обратимся к потерям, связанным с ошибочным решением задачи. Эта ошибочность зависит от объема имеющейся информации и обратно пропорциональна ему. Чем меньше информации, тем больше вероятность ошибки и тем значительней риск (напомним, что риск есть средние потери в результате ошибки). Именно поэтому на рисунке график риска R имеет убывающий характер.

Общие затраты, связанные с решением этой задачи, следует определить в виде суммы R+W, график которой, как видно, имеет четко выраженный минимум в точке Т^*. Это и есть оптимальный объем наблюдения.

Действуя таким образом, мы гарантируем себе в среднем минимальные суммарные потери, несмотря на то, что будем иногда ошибаться. Но эти ошибки принесут меньше вреда, чем от сбора информации.

Это и является теоретическим основанием права на ошибку. Ошибаться можно, но надо трезво оценивать потери, связанные с этой ошибкой.

Более того, ошибаться нужно! Если человек или какое-либо решающее устройство работают абсолютно без ошибок, можно смело утверждать, что они работают неоптимально. Без ошибок можно работать лишь в двух случаях: если работать очень медленно, то есть слишком долго фильтровать информацию, и если иметь огромную избыточную надежность, скажем, решать поставленную задачу параллельно несколькими способами, а потом принимать, решение голосованием. Оба случая связаны с огромными, ничем не оправданными затратами.

Вместе с тем не следует ударяться и в другую крайность - заставлять делать ошибки. Нужно помнить о риске, который образуется из двух факторов - стоимости ошибки и ее вероятности. Если ошибка стоит мало, то риск невелик и можно допустить сравнительно большое число ошибок. Если же стоимость ошибки велика, например в случае аварии, то ее вероятность следует сделать очень малой путем повышения надежности системы.

Хочется закончить этот параграф словами известного кибернетика Эшби, который в одном из своих выступлений сказал:

"...Гораздо дешевле и легче создать кибернетическую машину не со 100-процентной точностью, а с точностью, например, до 90 процентов и затем использовать ее, оценивая возможные ошибки ее функционирования на основе теории вероятностей. Достигаемый в этом случае выигрыш в цене и простоте создания такой машины (не абсолютно точной) весьма и весьма велик.

Очень часто люди, которые стремятся создать машины со 100-процентной точностью, затрачивают на это неимоверные усилия. Эти усилия не окупаются. Гораздо проще иметь машину менее точную, но такую, которую значительно легче сконструировать и которая также может быть использована".