6. Сосуществование со случайной помехой

Выше было показано, что всякое подавление случайных помех не может "додавить" их до конца. Всегда останутся случайные искажения, с которыми необходимо считаться. Значит, наш трижды случайный мир даже после подавления случайности останется, хотя и в меньшей мере, но все же случайным.

Естественно задать вопрос: а можно ли в таком неизбежно случайном мире получать очень точную информацию и совершать очень точные поступки? Короче, можно ли в обстановке помех действовать с малым и очень малым числом ошибок? Или мы обречены на безрадостную жизнь с постоянно высоким уровнем промахов?

Ответ на этот вопрос уже дала история развития человечества, история развития средств общения - языка и письма. Очевидно, что в мире, где действуют случайные помехи (неслучайные помехи не страшны - к ним всегда можно приспособиться и тем самым отключить), стихийно, в процессе эволюции, человечество должно было создать средства надежного общения, которые позволили бы осуществлять почти безошибочную связь между членами общества. Таким универсальным средством является избыточность.

Много ли информации в словах!

Давайте определим корреляцию между буквами в отдельных словах и между словами в отдельных предложениях.

Проведем простой эксперимент. Возьмите наугад десяток-полтора не очень сложных слов и попросите кого-нибудь угадывать последовательно каждую следующую букву слова. Если бы между буквами не было никакой связи, то относительное число угадываний было бы близко к нулю. А опыт показывает, что число угадываний большое и в среднем составляет более 50 процентов всех попыток. Это означает, что буквы в словах связаны между собой ярко выраженной зависимостью.

Чем ближе к концу слова, тем легче угадать букву, хотя можно и ошибиться. Так, седьмой буквой после шести "коров..." скорее всего будет "а", хотя не исключена и буква "н", если имелся в виду "коровник", а не "корова".

На рисунке 29 показано, как изменяется процент ошибок при угадывании первой, второй и т. д. букв различных слов. Хорошо видно, что в конце слова буквы почти не нужны - их легко угадывать. Причиной этому является высокая смысловая корреляция последних букв в слове с предыдущими. Этим свойством языка широко пользуются студенты при ведении к спектов лекций. Так, запись "Дв. им. дв. обм." легко интерпретируется как "Двигатель имеет двойную обмотку", хотя может быть расшифрована и иначе: "Дворник имел два обморока".

Рис. 29

Наличие корреляции делает наш язык избыточным и позволяет довольно легко угадывать слова даже при большом числе ошибок и описок. Указанная избыточность является хорошей защитой от действия случайных помех. Так, получив телеграмму со словами "...целую лампочку", довольно легко догадаться, что корреспондент хочет поцеловать "лапочку", а не "лампочку".

Если проделать тот же эксперимент со словами в фразе, то результат (вероятность угадывания) получится не столь сильным, но вполне чувствительным. Вероятность угадывания слова в среднем русском тексте равна примерно ¹/₁₀, то есть угадывается примерно одно из десяти слов.

Эта величина, правда, колеблется в значительных пределах для различных текстов. Так, специальная литература имеет очень большую избыточность, которая и облегчает ее беглый просмотр и чтение на незнакомом языке. Особо избыточны разговоры по радио между пилотом и дежурным на аэродроме. Здесь подобная избыточность связана с тяжелыми или даже трагическими последствиями ошибок, вероятность которых при высокой избыточности крайне мала. Наименьшую избыточность, то есть наименьшую корреляцию между словами, имеет язык художественных произведений за счет нестандартности, яркости и неожиданности речи писателей.

Интересно сравнить избыточность написанного текста и живой устной речи. Оказывается, последняя имеет большую избыточность, чем письменная речь. Действительно, в разговоре всегда много повторений, меньше заботы о "красоте стиля" и много "лишних слов", дающих говорящему возможность обдумать, что сказать дальше.

Но живая речь обладает возможностями, недоступными письменной. Она позволяет сообщать дополнительную информацию в виде ударений, в интонации, в индивидуальной особенности голоса. Эта дополнительная информация может составлять 50-70 процентов "смысловой информации", что понижает избыточность устной речи. Так, фраза "Что ты сделал?" в зависимости от постановки ударения может иметь различный смысл.

Избыточность - способ повышения надежности

Что такое избыточность при организации канала связи?

Это прежде всего такая система кодирования сообщений, при которой ошибки, допущенные при передаче или приеме, могут быть исправлены.

Существует два подхода к решению этой задачи. В одном подходе предлагается к передаваемому сообщению добавлять контрольный знак, позволяющий проверить правильность приема этого сообщения. Если допущена ошибка и по контрольному знаку обнаружена, то принимающий переспрашивает передающего и просит повторить тот кусок сообщения, в котором обнаружена ошибка. Такие системы связи носят название связи с переспросом.

Примером подобной связи является телеграф. Например, в обычной телеграмме всегда указывается число слов. Его можно использовать как контрольный знак, позволяющий хотя и грубо, но проверить правильность телеграммы. Действительно, пересчитав число слов в телеграмме и сравнив ее с контрольной суммой, легко проверить эффективность работы телеграфной связи. Если число слов окажется меньше контрольной суммы, то ясно, что в телеграмме потеряны слова. Правда, такая проверка очень груба и не дает возможности отличить две разные телеграммы с одинаковым числом слов. И все же это проверка.

Другой подход к решению задачи о надежной связи заключается в создании специального кода, который позволял бы не только обнаруживать ошибки, но и самостоятельно исправлять их, не запрашивая пункт передачи сообщения. Такой код называется самокорректирующимся, или кодом с исправлением ошибок.

Примером его может служить обычный человеческий язык, позволяющий исправлять орфографические ошибки сообщения без обращения к тому, кто передал сообщение, а возможно, и сделал ошибку. Приняв, допустим, сообщение - карова, можно смело исправлять его на корову, но для этого корректирующее устройство должно быть знакомо с грамматикой, правилами и исключениями русского языка.

Рассмотрим каждый способ в отдельности.

Канал с переспросом

Основной задачей здесь является обнаружение ошибки, поскольку сам по себе "переспрос" не представляет трудности. Каким же образом можно закодировать сообщение, чтобы иметь возможность обнаружить ошибку?

Будем рассматривать так называемый двоичный код, в котором имеется только два символа 0 и 1. Пусть 6 соответствует отсутствию сигнала в канале связи (пауза), а 1 соответствует сигналу. (Заметим, что известный код Морзе - знаменитая азбука Морзе - типичный пример троичного кода, состоящего из трех символов: точка, тире и пропуск.)

Всякий код состоит из блоков с одним и тем же числом символов. Например, для кодирования русского алфавита можно предложить блок из пяти символов:

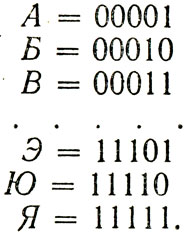
Примеры символов

Этот код полностью лишен избыточности.

Действительно, сообщение "ЭВА ЯВА", которое кодируется следующим образом: "111010001100001 111110001100001", теряет смысл при наличии хотя бы одной ошибки. Это означает, что при подобном кодировании ошибки не выявляются. Как повысить избыточность этого кода, чтобы суметь исправлять допущенные ошибки?

Первый пришедший в голову простейший прием заключается в дублировании, то есть предлагается каждый сигнал повторять дважды. В таком дублированном коде то же сообщение будет выглядеть так:

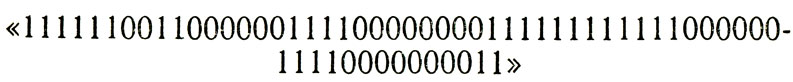
Вид сообщения

Эта мера действительно даст возможность выявить ошибку, если будет замечено, что в такой-то паре сигналов символы не совпадают. Но тогда понадобилось бы удвоить число символов. А это слишком дорогая плата за повышение надежности сообщения. Давайте прикинем, что дает дублирование.

Эффективность введенной избыточности естественно характеризовать двумя числами:

1. Числом (или процентом) неисправленных, пропущенных ошибок.

2. Удлинением кода (в процентах).

Очевидно, что для хорошего кода оба этих числа должны быть достаточно малыми.

В случае простого дублирования удлинение кода равно 100 процентам (код удваивается).

Теперь определим число пропущенных ошибок при дублировании.

Пусть помехи в канале связи изменяют передаваемый символ на обратный (вносят ошибку) в среднем в одном символе из ста. В этом случае говорят, что канал связи работает с вероятностью ошибок, равной одной сотой (¹/₁₀₀).

Ошибка при дублировании останется незамеченной только в том случае, если изменятся на обратный оба символа - основной и дублирующий. Вероятность того, что один из них будет передан неверно, равна ¹/₁₀₀.

Но одиночная ошибка будет немедленно исправлена после переспроса. Команда на переспрос появится, как только основной символ и его дублирующий не совпадут. Если же оба символа совпадают, то переспроса не последует и ошибка будет пропущена.

Очевидно, что это событие (две ошибки подряд) встречается значительно реже, чем одна ошибка, - в данном случае в сто раз реже. Следовательно, при дублировании из ста ошибок в среднем лишь одна будет пропущена, а остальные исправятся. Итак, в рассмотренном примере дублирование уменьшает процент ошибок в сто раз. Это очень хорошо. Но получено это слишком дорогой ценой - двукратным увеличением длины кода.

Поэтому простое дублирование текста сообщения хотя и применяется, но не является оптимальным способом повышения избыточности. Рассмотрим другой, более экономный способ.

Будем добавлять к блоку еще один символ, равный единице, если сумма чисел этого блока равна нечетному числу, и нулю, если эта сумма четна (нуль тоже четное число). Тогда для рассмотренного выше примера получим:

Для буквы А: 0 + 0 + 0 + 0 + 1 = 1 - нечетное число, поэтому к коду справа следует добавить единицу, и новый блок имеет вид А = 000011.

Для буквы В: 0 + 0 + 0 + 1 + 1 = 2 - четное число, следовательно, новый блок для В запишется так:

Теперь новый код принимает вид:

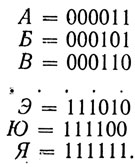
Новый код

Данный код уже имеет так называемую контрольную сумму (последний символ каждого блока). Эта сумма и позволяет проверить правильность передачи сообщения путем проверки каждого блока на четность и сопоставления результата с контрольной суммой.

Помехи в канале связи или в приемном и передающем устройствах могут изменить символ на обратный, то есть 0 сделать 1 или, наоборот, 1 сделать 0. Как легко убедиться, указанная выше проверка на четность позволяет выявить одиночную ошибку, поскольку а изменяет четность. Если же в одном блоке произошло две ошибки, то четность не изменится и ошибка не будет замечена. Аналогично три ошибки в блоке дадут сигнал на переспрос и исправление ошибки, а четыре пройдут незамеченными и т. д.

Следовательно, проверка на четность позволяет выявить не все ошибки. Часть из них так и останется незамеченной. Естественно определить: а велика ли эта часть? Какой процент ошибок не удается выявить при таком способе введения избыточности?

Давайте определим процент пропущенных ошибок при кодировании с контрольной суммой. Пусть, как и в предыдущем случае, канал связи передает каждый символ с вероятностью ошибки, равной ¹/₁₀₀ (в среднем одна ошибка на сто правильно переданных символов).

Рассмотрим один блок. Теперь состоит не из пяти, а из шести символов - добавлена контрольная сумма, которую тоже нужно правильно передавать. Пусть в этом блоке один символ был передан неправильно. Тогда, если все остальные символы, включая контрольную сумму, будут переданы правильно, то четность нарушится. Это немедленно установит контрольное устройство и отдаст команду на переспрос, в результате чего ошибка будет устранена.

Если же один из остальных пяти символов тоже был передан ошибочно, то четность не нарушится и ошибка будет пропущена. Как часто это будет происходить?

Если вероятность ошибки в одном символе равна ¹/₁₀₀, то вероятность ошибки в одном из пяти символов будет примерно в пять раз больше. Действительно, число возможностей для ошибок увеличивается, а значит, соответственно увеличивается и вероятность ошибки, которая в этом случае равна ¹/₂₀ (одна повторная ошибка в том же блоке на двадцать одиночных).

Это означает, что число ошибок при подобном введении избыточности уменьшается примерно в 20 раз.

Следовательно, проверка на четность дала в этом случае возможность повысить эффективность кода в 20 раз! Соответственно в 20 раз снижена роль случайных помех. Причем, как видно, никаких попыток снизить уровень помех в данном случае не производилось. Канал связи остался тем же, с той же одной ошибкой в среднем на сто передаваемых символов. Этот великолепный результат получен только за счет эффективного кодирования, то есть за счет введения проверки блоков кода на четность. Длина кода при этом возросла лишь на 20 процентов (один добавочный символ на пять символов одного блока).

Рассмотренные методы введения избыточности позволяют ценой некоторого удлинения кода значительно повысить его надежность и эффективно использовать при передаче сообщений по каналам связи, в которых действует случайная помеха.

Полезность применения такого рода избыточности для передачи телеграфных сообщений очевидна. Но этот метод может быть использован и в других ситуациях, внешне ничем не похожих на телеграфную задачу. Так, одним из приложений избыточности могут служить современные быстродействующие вычислительные машины.

Обильную пищу для введения избыточности предоставляет эксплуатация вычислительных машин. Необходимость избыточности здесь диктуется двумя "шумящими" факторами:

1) человеком, обслуживающим машину, и 2) ненадежностью самой машины.

Чтобы понять, почему "шумный" (ошибающийся) человек, обслуживающий вычислительную машину, может повлиять на эффективность работы машины, рассмотрим, как вводится информация в современную вычислительную машину.

Для решения поставленной задачи в вычислительную машину необходимо ввести информацию о том, "как считать" и "что считать".

Первый вопрос связан с созданием программы работы машины для решения поставленной задачи и с введением этой программы в вычислительную машину, в виде определенных числовых кодов типа тех, избыточность которых рассматривалась выше.

Так, например, чтобы решить уравнение ах⁴ + bх³ + сх² + dx + е = 0 на универсальной вычислительной машине, необходимо составить программу работы этой машины (как считать) и ввести ее в машину. Вторая категория информации, вводимой в машину, отвечает на вопрос "что считать" и составляет все исходные данные для необходимого расчета. Так, в указанном примере исходными данными являются заданные значения коэффициентов этого уравнения, то есть числа а, b, с, d, е.

Вся эта информация может вводиться в машину различными способами. Ее могут вводить оператор, перфолента и перфокарта.

Оператор на пульте - это самый неэффективный способ введения информации в машину, поскольку оператор работает слишком медленно.

Перфолента - так называется бумажная или целлулоидная лента с дырочками (перфорацией), которые несут в определенном коде необходимую информацию в машину. Каждая дырка соответствует единице кода, а ее отсутствие - нулю этого кода. Эту ленту вставляют в специальное "Устройство ввода" вычислительной машины, где она протаскивается с большой скоростью между рядами лампочек и фотоэлементов. Каждая дырка перфоленты, проходя мимо фотоэлемента, пропускает световой импульс, который и вызывает соответствующий ему импульс тока в фотоэлементе. Так, в машину вводится "1" кода. "0" получается при отсутствии импульса.

Это очень эффективный способ введения информации в машину, так как перфоленту можно протаскивать с большой скоростью через вводное устройство.

И наконец, перфокарты - бумажные карты (раза в три больше обычных игральных) - с дырками, при помощи которых кодируется информация. Колода перфокарт и несет в себе все необходимые для расчетов сведения. В настоящее время перфокарты являются наиболее эффективным способом введения информации в машину. Дело тут в том, что перфокарту устройство считывает сразу всю целиком, что значительно убыстряет ввод информации в машину. С другой стороны, программу на перфокартах очень удобно переделывать - для этого достаточно заменить одну-две перфокарты на новые. Перфоленту в этом случае нужно клеить, и клеить очень аккуратно, так как ей предстоит с большой скоростью двигаться во вводном устройстве.

Всем хороши перфокарты! Но...

Тут есть одно "но"...

Печальный рассказ со счастливым концом

Все дело в том, что дырки на перфокартах делаются, так сказать, при непосредственном вмешательстве "человеческого разума". Чаще всего их пробивают милые тихие девушки, обычно выпускницы средних школ, и их интересует все, что должно" интересовать молодых девушек в их возрасте. Они сидят за перфоратором (прибором для пробивания дырок в перфокарте, который умеет делать дырки, но не знает, где их поставить), смотрят в программу, написанную программистом (тоже грешным человеком), и нажимают на клавиши аппарата, пробивая тем самым отверстия в перфокарте.

Поскольку эта работа очень монотонная, то девушки обычно переговариваются между собой на всякие темы, Время от времени из перфоратора выпадает готовая перфокарта, которая несет необходимую для машины информацию и... ошибки.

Если взять эти перфокарты и ввести в машину (так это и делается), то жизнь оператора и программиста сразу окрасится в мрачные тона (так это и бывает). Все, кажется, в порядке - программа проверена несколько раз машина работает превосходно (все тесты выполнены без ошибок), а задача не идет!

А виной всему симпатичная девушка-перфораторщица, которая и думать забыла про эту задачу, сейчас а набивает новую, обсуждая новый фильм и делая новые ошибки.

Если внимательно присмотреться к этой ситуации, то нетрудно заметить, что наша девушка является каналом связи между написанной от руки программой и машиной (рис. 30). Причем канал этот имеет собственные случайные помехи, которые трудно подавить (если вы ее отругаете - она расплачется, а не дадите премии - уйдет). Вот и приходится мириться с этим источником случайных ошибок в перфокартах и выявлять их при отладке программы на машине. А это очень тяжелая задача.

Рис. 30

Но если всему виной канал связи с помехами, которые нельзя отфильтровать, то не воспользоваться ли изложенным выше способом кодирования с проверкой на четность? Ведь позволяет выявить практически почти все ошибки, возникающие в канале связи!

Так пришли к выводу, что нужно ввести проверку на четность в самой перфокарте. Чтобы понять, как это сделать, рассмотрим одну перфокарту. Состоит она обычно из 80 вертикальных колонок. В колонках пробиваются отверстия (рис. 31), которые в определенном коде (неважно каком) несут информацию.

Рис. 31

Последняя строка перфокарты контрольная. В ней делается дырка, если сумма дырок в соответствующей колонке нечетная, и не делается - если соответствующая сумма дырок четна. Контрольная строка заранее определяется программистом и записана им в программе.

В перфоратор встроено несложное устройство, которое делает проверку указанных блоков - колонок на четность, точно так же, как было показано выше.

Если проверка не оправдывается: сумма четна, а на контроле дырка - или наоборот, - то включается звонок, извещающий о том, что кем-то (программистом или перфораторщицей) допущена ошибка.

Выяснить, кто виноват, довольно легко: нужно просто вычислить, а затем либо молча перебить перфокарту, либо устроить скандал программисту, который не сумел отличить четное число от нечетного.

И все довольны! Доволен программист - ему не нужно искать чужих ошибок в программе; довольна девушка - ее больше не ругают и даже дали возможность высказываться в адрес программиста; доволен оператор - не нужно обуздывать "одичавшую" машину; доволен и дежурный инженер - меньше упреков в адрес машины, а то чуть что - и все валят на машину, а она, конечно, не ого-го какая, но все же!..

Можно ли делать безошибочные вычисления на ошибающейся машине!

В ответ на этот вопрос мне однажды пришлось услышать весьма любопытное мнение. Речь шла о быстродействующих вычислительных машинах и об их неизбежных сбоях. Эти сбои портят кровь и характер всем, кому приходится сталкиваться с машинами. Дело в том, что современная вычислительная машина средней производительности и среднего качества сбивается примерно один раз в час работы. В жизни же весьма часто встречаются задачи, на решение которых приходится тратить десятки и даже сотни часов машинного времени. Выходит, что задача наверняка будет решена с ошибкой! Отсюда делается вывод, что либо нужно отказаться от решения подобных "сверхзадач", либо для их решения нужно создавать машины, которые имеют один сбой за 100-1000 часов непрерывной работы.

Спору нет, такие машины нужны, но правильно ли, что эти сверхзадачи нельзя решать на машинах, которые ошибаются "всего" в сто раз чаще? Давайте подумаем, как решать большую задачу на ненадежной машине.

Обычным приемом в этом случае является повторный счет. На первый взгляд кажется, что достаточно задачу решить несколько раз и если встретятся одинаковые результаты, то их и считать правильным решением.

А если вероятность правильного решения мала? Кстати, это так и есть для очень сложных задач. В этом случае машину придется "крутить" слишком долго, прежде чем будут получены два одинаковых результата.

Скажем, машина делает один сбой в среднем за один час работы. Нужно решить пятичасовую задачу, то есть такую задачу, на которую при безошибочной работе машины затрачивается 5 часов времени. Вероятность того, что машина ни разу не собьется в течение пяти часов, равна ¹/₃₂. (Действительно, вероятность безошибочного счета в течение одного часа равна ¹/₂. Вероятность двухчасовой работы без ошибок будет равна в два раза меньше и т. д.) Это значит, что для получения одного правильного решения пятичасовой задачи нужно в среднем 32 раза решить эту задачу. А всего будет затрачено примерно: 32×5=160 часов!

Более месяца пришлось бы решать пятичасовую задачу (по 7 часов в день)! Есть над чем задуматься: может быть, правы скептики, утверждающие, что подобные задачи нам еще не по зубам, что нужно еще дорасти до этих задач, а поэтому "неча на зеркало пенять, коли..." не умеем делать хороших и надежных вычислительных машин.

Однако если разобраться, то 160 часов - это неоправданная и бесхозяйственная плата за... недомыслие.

Нужно ли повторять все решение? Может быть, пересчитывать лишь небольшие куски, где мог произойти случайный сбой? Это и есть ключ к решению!

Разобьем задачу на несколько последовательных этапов. Начнем с первого и будем пересчитывать его до тех пор, пока результаты не совпадут. После этого можно быть уверенным, что первый этап решен правильно (вероятность одинаковых ошибок практически равна нулю и может не учитываться). Далее переходим к вычислению второго этапа и так же повторяем его до совпадения двух вариантов расчета. Переходим к третьему этапу задачи и т. д.

Проиллюстрируем эффективность такого подхода на том же примере пятичасовой задачи, решаемой на той же машине, которая делает в среднем все ту же одну роковую ошибку в час. Разобьем эту задачу, например, на пять одночасовых этапов. На каждом таком этапе машина ошибается в половине всех случаев. Поэтому одно правильное значение будет получено в среднем за два прогона, и, следовательно, для двух правильных решений нужно сделать в среднем примерно четыре просчета. Тогда общие затраты будут иметь вид:

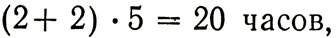
то есть в 8 раз меньше, чем при первом варианте решения той же задачи.

Но это еще не наилучший вариант!

На ненадежных машинах можно решать, и очень большие задачи. Нужно только уметь разбивать их на оптимальное число этапов.

Таким образом, применение специальных приемов для решения больших задач дает возможность пользоваться ненадежными вычислительными машинами. Это тоже преодоление случайного фактора, но не путем его подавления (машина как ошибалась раньше, так продолжает ошибаться в том же духе), а путем специальной организации работ на машине.

Теперь рассмотрим коды с исправлением ошибок, или самокорректирующиеся коды. Они имеют несомненное преимущество перед кодами, работающими в канале с переспросом. Действительно, в последнем случае нужно иметь обратную связь, позволяющую осуществить переспрос. А это очень дорогое удовольствие, так как требует удвоения приемо-передаточной аппаратуры для организации канала переспроса и прерывания передачи для ответа на переспрос.

Применение самокорректирующихся кодов упрощает приемо-передаточные устройства, которые работают в программном режиме (без обратной связи). Правда, покупается это ценой значительного усложнения декодирующей аппаратуры и усложнением самого кода, что является платой за отсутствие обратной связи.

"Самолечение" кодов

Самокорректирующиеся коды являются типичным примером избыточности с самовосстановлением, когда в код закладывается информация о том, как его можно восстановить, если случайные помехи изменят его.

Как и раньше, будем рассматривать код, состоящий из отдельных блоков, и помнить, что нам достаточно рассмотреть самовосстановление одного блока.

Пусть блок имеет к символов и представляет собой следующую последовательность:

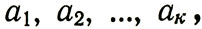
где каждый символ а₁,как обычно, принимает одно из двух значений - ноль или единицу:

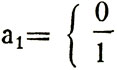
при всех i=1, 2, ..., к.

Для работы в канале с переспросом этот код мы дополняли одним символом - четностью b, который выражался следующим образом через символы блока:

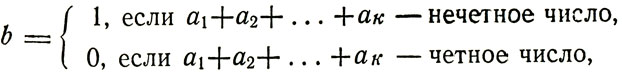
а новый блок записывался в виде:

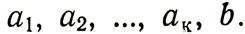
Символ четности b просто приписывается к исходному блоку справа.

Как мы убедились, это дает возможность обнаружить наличие ошибок в блоке, если число ошибок нечетно. И для ответа на вопрос, где именно расположена эта ошибка, необходимо было сделать переспрос: следовало остановить дальнейшую передачу сообщения (для этого понадобилась обратная связь) и заняться ее исправлением.

Для создания кода с возможностью исправления ошибок без переспроса по каналу обратной связи рассмотрим блок конкретной длины к, например, к=12.

Назовем его основным блоком. Расположим этот блок не в виде последовательности, а в виде таблицы, или, как говорят, матрицы:

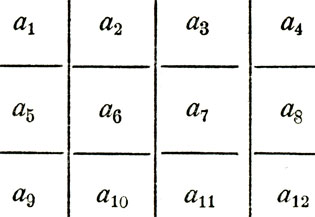
Матрица

А теперь определим четность всех строк и всех столбцов этой матрицы, приписав символы четности по ее краям:

Четность матрицы

где b₁, b₂, b₃ - четность строк, a b₄, b₅, b₆, b₇ - четность столбцов, то есть

Теперь избыточный блок можно получить, считывая последовательно строки дополнительной матрицы: a₁ a₂ a₃ a₄ b₁ a₅ a₆ a₇ a₈ b₂ a₉ a₁₀ a₁₁ a₁₂ b₃ b₄ b₅ b₆ b₇. Например, блок

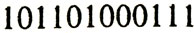
можно записать в виде матрицы

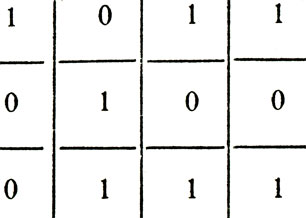
Матрица

которую можно дополнить символами четности

Матрица, дополненная символами четности

И полученный избыточный блок равен

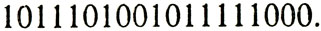
Теперь, если в качестве нового блока выбрать последнюю избыточную матрицу, дополненную семью символами четности b₁, b₂, ..., b₇, то ошибки можно восстанавливать без переспроса.

Действительно, пусть ошибка закралась в основной блок а₁, а₂, ..., a₁₂. Тогда изменение одного символа на обратный приведет к нарушению четности в строке и столбце, соответствующих этому символу. Следовательно, если ошибка коснулась основного блока, то нарушатся два условия четности. По ним легко восстановить правильное значение символа. Для этого достаточно символ, стоящий на пересечении строки и столбца с нарушенными четностями, изменить на обратный. Вот и вся корректировка.

Например, в результате помех в канале связи был принят следующий блок:

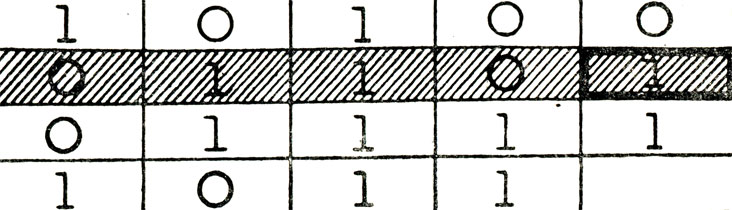
Рис. 32

Проверка показывает, что нарушается четность в первом столбце и последней строке основного блока. Это означает, что символ ад, стоящий на их пересечении, принят ошибочно и должен быть изменен на обратный, то есть должно быть a₉=1. И блок исправлен.

Но ошибка может быть и в символах четности b₁, b₂, ..., b₇. Тогда нарушится лишь одно условие четности, что говорит об ошибке в символе четности.

Например, полученный блок после представления в матричной форме имеет вид:

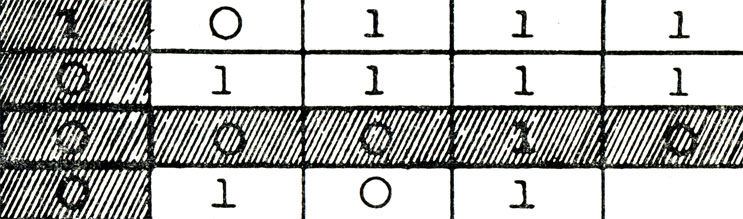
Рис. 33

Здесь нарушается четность только во второй строке. Это означает, что ошибка в символе четности b₂, который должен быть изменен на обратный: b₂=0.

Мы рассмотрели наиболее простой случай, когда в блоке имеется одна ошибка. Можно построить код, позволяющий исправить две, три и т. д. ошибок. Для этого нужно делать дополнительную проверку на четность (например, по диагоналям или ходом шахматного коня и т. д.).

Вводя указанную проверку на четность, можно построить самокорректирующийся код с любой надежностью. Но при этом увеличивается объем кода. Так, в рассмотренном примере основной блок к=12 вырос при введении избыточности до к=12+7=19, то есть на 60 процентов. Не слишком ли это много?

Нет, не слишком. С увеличением объема основных блоков этот процент уменьшается. Для к=100 (матрица 10×10) потребуется 20 проверок на четность, и тогда избыточный блок будет содержать 120 членов, то есть объем возрастет лишь на 20 процентов. С ростом к это число будет еще более уменьшаться.

Таким образом, с точки зрения экономности кода удобнее иметь большие блоки. Допустим, кодировать не буквы - их всего 32, а целые слова, которых значительно больше. Объем каждого блока при этом увеличивается.

Изложенные выше соображения позволяют утверждать (впервые это доказал знаменитый Клод Шеннон, создатель теории информации), что для любого канала связи с любым уровнем ошибок всегда можно построить такой самокорректирующийся код, который обеспечит надежность передачи сообщений, сколь угодно близкую к абсолютной. Естественно, что повышение надежности передачи связано с уменьшением ее скорости, так как объем кода при этом возрастает.

В заключение отметим, что коды с исправлением ошибок являются блестящим примером самовосстанавливающихся систем, избыточность которых обеспечивает их неизменность даже при действии значительных случайных помех. Это весьма эффективная борьба со случайностью, но не путем ее подавления, а за счет выбора разумного образа поведения в обстановке помех, который позволяет действовать весьма надежно в очень "ненадежной" обстановке.