3. Случай и игра

Широкое поле для исследования роли случайности открывается в игровых ситуациях. Под игрой подразумевается взаимодействие двух сторон, имеющих противоположные интересы и действующих в рамках определенных правил. Повышенный интерес, проявляемый в последнее время к теории игр, объясняется ее применением к решению задач, возникающих во многих важных конфликтных ситуациях, в частности в военных конфликтах.

Оказывается, детские игры, такие, как игра в жмурки, в палочку-выручалочку и другие, игры взрослых, например картежные, в простой и незатейливой форме моделируют конфликтные взаимоотношения сторон, скажем, двух государств, нескольких фирм и т. д.

Самым существенным и определяющим в игре являются антагонистичность и активность партнеров.

Несложно обыграть противника наивного и неизобретательного. В таком случае можно предпринять ход, прямо рассчитанный на его недогадливость. Ну а если он только прикидывается простодушным и решил подстроить хитрую ловушку и поставить вас в безвыходное положение? Так неопытные шахматисты часто проигрывают из-за того, что делают "соблазнительные" ходы, надеясь на то, что противник не заметит угрозы. Вывод один: нельзя рассчитывать на ошибку, пассивность или недомыслие противника; необходимо исходить из того, что он умен, осторожен и так же страстно жаждет выигрыша.

Простейшая схема ситуаций, рассматриваемых в теории игр, чрезвычайно проста. В игре участвуют два человека, интересы которых строго противоположны. Представим себе, что в каждом квадрате прямоугольной таблицы или на каждом поле шахматной доски написано какое-то определенное число. В соответствии с правилом игры один игрок (А) должен выбрать строку, другой (Б) - столбец этой таблицы. Результат этих двух выборов определяет число, находящееся в месте пересечения указанных строк и столбцов. Предполагается, что каждый игрок делает выбор, не зная решения противника.

Если на пересечении стоит число со знаком плюс, то выигрывает А, а Б столько же проигрывает, если со знаком минус - Б выигрывает у А, причем размеры выигрыша зависят от величины числа. К подобной простой схеме сводится огромное множество конфликтных ситуаций, встречающихся в жизни.

Рассмотрим для примера игру с таблицей, изображенной на рисунке 46.

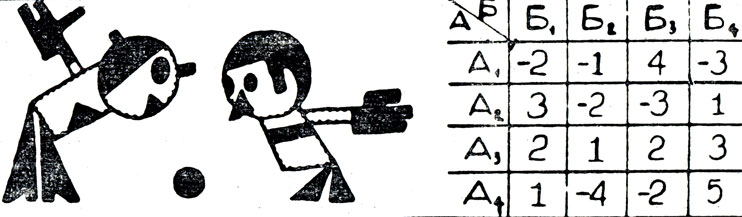
Рис. 46

Изучая ее, игрок А немедленно обратит внимание на свою четвертую строку, А₄, которая может дать ему максимально возможный выигрыш в 5 единиц, если Б сыграет четвертым столбцом Б₄. Но, поразмыслив, он поймет, что Б не дурак и на А₄ может ответить Б₂, выиграв 4 единицы. Аналогичные рассуждения относительно хода А и обещающего в лучшем случае выигрыш 4 единиц, приводят к грустному выводу о проигрыше при любом ответе противника, кроме Б₃.

Игрок А убеждается, что нечего мечтать о журавлях в небе, а достаточно удовлетвориться синицей в руках. И начинает искать ход, который гарантировал бы ему хоть малый, но выигрыш. Такой трезвый взгляд на вещи немедленно вознаграждается.

Изучив таблицу, он замечает, что в его распоряжении есть одна строка - А₃, которая всегда обеспечивает ему выигрыш независимо от хода противника. Это заметит и игрок Б, которому ясно, что при ходе его противника А₃ он всегда проигрывает. И ему ничего не остается делать, как постараться понести возможно меньшие потери и пойти Б₂. Таким образом, в данной игре один из игроков непременно выигрывает, другой (уж так получилось) проигрывает.

Сделав подробный анализ, игроки могут не играть, поскольку исход игры уже ясен. Такой вывод сделан потому, что определена оптимальная стратегия поведения обоих игроков и эта стратегия заключается в выборе А₃ для игрока А и Б₂ для Б, что однозначно характеризует результат игры. Смыслом теории игр как раз и является отыскание оптимальных стратегий.

Мы рассмотрели нехитрый пример, когда каждый игрок располагал всего лишь четырьмя вариантами ходов. А если этих вариантов очень много? Представьте себе, какое огромное число возможных вариантов ходов имеется у шахматиста и особенно в середине игры. А сколько вариантов должен рассмотреть заказчик, решая вопрос о размещении заказов на нескольких предприятиях!

Сейчас, чтобы просчитать все варианты в сложных ситуациях и определить Оптимальную стратегию, используются быстродействующие вычислительные машины. Они могут делать сотни тысяч арифметических операций в секунду. Но предварительно нужно правильно проанализировать обстановку и составить таблицу, аналогичную рассмотренной выше.

И вот тут-то мы и встречаемся с новым осложнением. Очень часто ситуация такова, что, сколько бы мы ни считали, мы не найдем оптимального варианта хода. Более того, оказывается, в играх такие ситуации весьма распространены и в подавляющем большинстве игр оптимального хода не существует. Это легко объяснить. Если существует оптимальный ход, то игру не имеет смысла продолжать (что и сделал игрок Б в изложенном выше примере). Интерес к игре немедленно пропадает, как только выясняется существование наилучшего хода. Именно поэтому все интересные игры не имеют наилучших ходов. Примером может служить широко известная игра в сравнение монет.

Сыграем в орлянку

Наверное, многие знают, в чем заключается смысл игры в орлянку. Оба игрока независимо друг от друга выбирают цифру или герб своих монеток и после этого сверяют их. Если выбраны одинаковые стороны монет (две цифры или два герба), то выигрывает игрок А, игрок Б выплачивает ему одно очко. При выборе разных сторон (герб и цифра) выигрывает игрок Б, и теперь он получает от А одно очко. Казалось бы, совсем просто.

Таблица (рис. 47) имеет всего лишь два варианта для каждого игрока! Но, оказывается, это не так. И если в предыдущем случае можно было уверенно выбрать стратегию поведения - она сводилась к выбору наилучшего хода, - то здесь игрокам придется призадуматься.

Рис. 47

Действительно, пусть игрок А решил действовать по какой-то определенной стратегии, например, пусть он выбирает два раза герб, а затем один раз цифру. Ясно, что как только Б заметит эту закономерность, он тут же выберет контрстратегию: два раза цифра - один раз герб - и начнет уверенно выигрывать.

Если игрок А выберет стратегию посложней, то игроку Б будет труднее разгадать ее. Но как только он узнает, какова эта стратегия, он опять начнет выигрывать. А до тех пор пока стратегия А еще не разгадана, игроку Б нужно выжидать и делать ни к чему не обязывающие ходы - лишь бы не проигрывать. Для этого ему достаточно играть случайно, подбрасывая вверх монетку и доверяя выбор своего хода случаю. Тогда его проигрыш или выигрыш будут случайными, но в среднем равными нулю. При этом он должен пристально наблюдать за игрой своего противника, чтобы установить его стратегию. Как только он ее определит, так сразу же выработает контрстратегию и начнет систематически выигрывать.

Следовательно, игрок А, играющий по определенной, как говорят, детерминированной, стратегии, оказывается всегда в худшем положении. В самом деле, пока игрок Б "расшифровывает" его стратегию, он может и выигрывать и проигрывать, но после расшифровки А ждет неизбежный проигрыш.

Но почему же это так? Почему в проигрыше всегда игрок А? Ведь оба игрока в совершенно равном положении!!!

Дело в том, что игрок А старался добиться выигрыша при помощи детерминированной стратегии. Он играл по строго выбранному правилу, которое игрок Б расшифровал. За время расшифровки оба они находились в равном положении, зато после расшифровки А сразу проиграл.

Может быть, ему следует почаще менять стратегию игры, чтобы игрок Б как можно больше времени тратил на расшифровку? Оказывается, и это его не спасет. Опять ситуация та же. Во время расшифровки оба игрока в равном положении, но сразу же после расшифровки Б уверенно выиграет.

Читатель, наверное, уже заметил, что в этой игре есть периоды, когда игроки в равном положении, а именно, когда выигрыш или проигрыш определяется совершенно случайными ходами. И как ни странно покажется с первого взгляда, стратегия совершенно случайных ходов и является в данной ситуации наилучшей (оптимальной) стратегией поведения обоих игроков.

Игрок А наказывался неизбежным проигрышем именно за то, что он действовал неоптимальным образом и пытался воспользоваться детерминированной стратегией. Наилучшей формой поведения в рассмотренной игре является случайная стратегия, которая хотя и не приносит уверенного выигрыша, но и не дает такой возможности противнику. Он не знает, да и не может знать в силу случайной стратегии, какой ход сделает его противник. Поэтому очень часто в конфликтных ситуациях элемент случайности играет роль дымовой завесы, ставящей в тупик противника и парализующей его целенаправленные действия.

Игра в секреты

Хорошим примером подобной ситуации является расшифровка секретных кодов. Положение здесь такое же, как в только что рассмотренной игре. Всякий шифр можно раскрыть, определив закономерность в передаваемых знаках. По существу, сложные шифры - это тоже дымовая завеса, предоставляющая одной стороне определенный выигрыш во времени, которое противник тратит на дешифрование. Здесь тоже имеются два противника: шифровщик, стремящийся скрыть смысл передаваемого сообщения, и дешифровщик противника, раскрывающий содержание сообщения.

На первый взгляд эта игра явно невыгодна шифровщику, так как он волей-неволей должен передавать осмысленные сообщения, которые противник всегда может расшифровать. При этом дешифровщик опирается на следующее известное положение теории информации: любой код можно расшифровать, если, во-первых, имеется достаточно длинное сообщение, зашифрованное этим кодом, и, во-вторых, если сообщение имеет смысл. Шифровщику это положение также известно, и он старается так закодировать информацию, чтобы вражеский дешифровщик затратил как можно больше времени на декодирование. Так обычно и поступает всякая секретная служба, передавая важные сообщения.

Наиболее эффективным приемом зашифровки смысла является, как это ни парадоксально, полное отсутствие смысла. Для этого либо пользуются чисто случайным кодом, либо передают бессмысленный набор букв или слов.

Правда, подобный метод скрывает смысл передачи не только от противника, но и от своего адресата. Поэтому случайным кодом пользуются лишь время от времени, перемежая его с осмысленным. Такой способ шифровки доставляет наибольшие неприятности противной стороне. Получив сообщение, ее дешифровщик должен прежде всего решить, есть смысл в нем или нет, либо определить, какая часть всего сообщения несет смысл, а какая случайная. Это как раз и является наиболее сложной задачей, на решение которой затрачивается много времени. Сам же процесс расшифровки, как правило, не занимает много времени, так как проводится он на быстродействующих вычислительных машинах.

Подводя итог, можно сказать, что элемент случайности в конфликтных ситуациях играет решающую роль. Он является той надежной мерой, которая сковывает активность противника и не позволяет ему добиться преимущества. Это обстоятельство заставляет вводить случайный фактор там, где детерминированное поведение приводит к проигрышу.

Такой наиболее характерной областью применения элемента случайности является военное дело. При любом столкновении противников отыскивается оптимальное поведение, которое часто оказывается случайным. В ряде экономических ситуаций - особенно в условиях капиталистической конкуренции - часто выигрывает тот, кто примет случайную стратегию поведения.

Широкое применение элемента случайности в конфликтных ситуациях основано на трезвом расчете и твердой уверенности, что случайная стратегия наиболее целесообразна и приводит к оптимальным решениям. А неудачником оказывается тот, кто не верит в оптимальность случая.